В 1900 году один из величайших ученых прошлого столетия Давид Гильберт составил перечень, состоящий из 23 нерешенных проблем математической науки. Работа над ними оказала колоссальное влияние на развитие этой области человеческого знания. Спустя 100 лет Математический институт Клэя представил список из 7 проблем, известных как задачи тысячелетия. За решение каждой из них была предложена премия в 1 миллион долларов.
Единственной задачей, которая оказалась в числе обоих перечней головоломок, уже не одно столетие не дающих покоя ученым, стала гипотеза Римана. Она еще ждет своего решения.
Краткая биографическая справка
Георг Фридрих Бернхард Риман родился в 1826 году в Ганновере, в многодетной семье бедного пастора, и прожил всего 39 лет. Ему удалось опубликовать 10 трудов. Однако уже при жизни Риман считался преемником своего учителя Иоганна Гаусса. В 25 лет молодой ученый защитил диссертацию «Основания теории функций комплексной переменной». Позже он сформулировал свою гипотезу, ставшую знаменитой.

Простые числа
Математика появилась, когда человек научился считать. Тогда же возникли первые представления о числах, которые позже попытались классифицировать. Было замечено, что некоторые из них обладают общими свойствами. В частности, среди натуральных чисел, т. е. таких, которые использовались при подсчете (нумерации) или обозначении количества предметов, была выделена группа таких, которые делились только на единицу и на самих себя. Их назвали простыми. Изящное доказательство теоремы бесконечности множества таких чисел дал Евклид в своих «Началах». На данный момент продолжается их поиск. В частности, самым большим из уже известных является число 274 207 281 – 1.
Формула Эйлера
Наряду с понятием о бесконечности множества простых чисел Евклид определил и вторую теорему о единственно возможном разложении на простые множители. Согласно ей любое целое положительное число является произведением только одного набора простых чисел. В 1737 году великий немецкий математик Леонард Эйлер выразил первую теорему Евклида о бесконечности в виде формулы, представленной ниже.
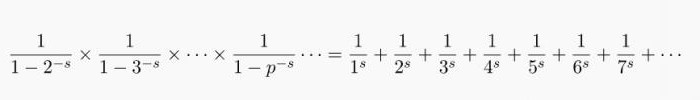
Она получила название дзета-функции, где s — константа, а p принимает все простые значения. Из нее напрямую следовало и утверждение Евклида о единственности разложения.
Дзета-функция Римана
Формула Эйлера при ближайшем рассмотрении является совершенно удивительной, так как задает отношение между простыми и целыми числами. Ведь в ее левой части перемножаются бесконечно много выражений, зависящих только от простых, а в правой расположена сумма, связанная со всеми целыми положительными числами.
Риман пошел дальше Эйлера. Для того чтобы найти ключ к проблеме распределения чисел, он предложил определить формулу как для действительной, так и для комплексной переменной. Именно она впоследствии получила название дзета-функции Римана. В 1859 году ученый опубликовал статью под заголовком «О количестве простых чисел, которые не превышают заданной величины», где обобщил все свои идеи.
Риман предложил использовать ряд Эйлера, сходящийся для любых действительных s>1. Если ту же формулу применяют для комплексных s, то ряд будет сходиться при любых значениях этой переменной с действительной частью больше 1. Риман применил процедуру аналитического продолжения, расширив определение zeta(s) на все комплексные числа, но «выбросив» единицу. Она была исключена, потому что при s = 1 дзета-функция возрастает в бесконечность.
Практический смысл
Возникает закономерный вопрос: чем интересна и важна дзета-функция, которая является ключевой в работе Римана о нулевой гипотезе? Как известно, на данный момент не выявлено простой закономерности, которая бы описывала распределение простых чисел среди натуральных. Риману удалось обнаружить, что число pi(x) простых чисел, которые не превосходили x, выражается посредством распределения нетривиальных нулей дзета-функции. Более того, гипотеза Римана является необходимым условием для доказательства временных оценок работы некоторых криптографических алгоритмов.
Гипотеза Римана
Одна из первых формулировок этой математической проблемы, не доказанной и по сей день, звучит так: нетривиальные 0 дзета-функции — комплексные числа с действительной частью равной ½. Иными словами они расположены на прямой Re s = ½.
Существует также обобщенная гипотеза Римана, представляющая собой то же утверждение, но для обобщений дзета-функций, которые принято называть L-функциями Дирихле (см. фото ниже).
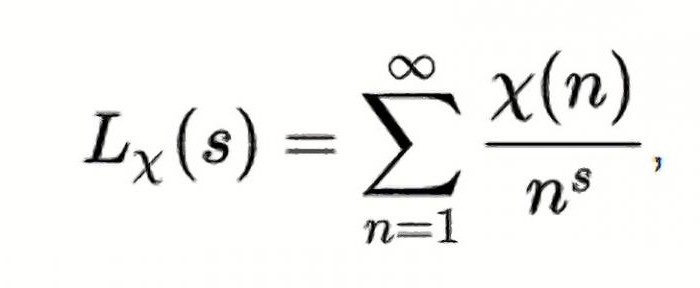
В формуле χ(n) — некоторый числовой характер (по модулю k).
Римановское утверждение считается так называемой нулевой гипотезой, так как была проверена на согласованность с уже имеющимися выборочными данными.
Как рассуждал Риман
Замечание немецкого математика изначально было сформулировано достаточно небрежно. Дело в том, что на тот момент ученый собирался доказать теорему о распределении простых чисел, и в этом контексте данная гипотеза не имела особого значения. Однако ее роль при решении многих других вопросов огромна. Именно поэтому предположение Римана на данный момент многими учеными признается важнейшей из недоказанных математических проблем.
Как уже было сказано, для доказательства теоремы о распределении полная гипотеза Римана не нужна, и достаточно логически обосновать, что действительная часть любого нетривиального нуля дзета-функции находится в промежутке от 0 до 1. Из этого свойства следует, что сумма по всем 0-м дзета-функции, которые фигурируют в точной формуле, приведенной выше, — конечная константа. Для больших значений x она вообще может потеряться. Единственным членом формулы, который останется неизменным даже при очень больших x, является сам x. Остальные сложные слагаемые в сравнении с ним асимптотически пропадают. Таким образом, взвешенная сумма стремится к x. Это обстоятельство можно считать подтверждением истинности теоремы о распределении простых чисел. Таким образом, у нулей дзета-функции Римана появляется особая роль. Она заключается в том, чтобы доказать, что такие значения не могут внести существенного вклада в формулу разложения.
Последователи Римана
Трагическая смерть от туберкулеза не позволила этому ученому довести до логического конца свою программу. Однако от него приняли эстафету Ш-Ж. де ла Валле Пуссен и Жак Адамар. Независимо друг от друга ими была выведена теорема о распределении простых чисел. Адамару и Пуссену удалось доказать, что все нетривиальные 0 дзета-функции находятся в пределах критической полосы.
Благодаря работе этих ученых появилось новое направление в математике — аналитическая теория чисел. Позже другими исследователями было получено несколько более примитивных доказательств теоремы, над которой работал Риман. В частности, Пал Эрдеш и Атле Сельберг открыли даже подтверждающую ее весьма сложную логическую цепочку, не требовавшую использования комплексного анализа. Однако к этому моменту посредством идеи Римана уже было доказано несколько важных теорем, включая аппроксимацию многих функций теории чисел. В связи с этим новая работа Эрдеша и Атле Сельберга практически ни на что не повлияла.
Одно из самых простых и красивых доказательств проблемы было найдено в 1980 году Дональдом Ньюманом. Оно было основано на известной теореме Коши.
Угрожает ли римановская гипотеза основам современной криптографии
Шифрование данных возникло вместе с появлением иероглифов, точнее, они сами по себе могут считаться первыми кодами. На данный момент существует целое направление цифровой криптографии, которое занимается разработкой алгоритмов шифрования.
Простые и «полупростые» числа, т. е. такие, которые делятся только на 2 других числа из этого же класса, лежат в основе системы с открытым ключом, известной как RSA. Она имеет широчайшее применение. В частности, используется при генерировании электронной подписи. Если говорить в терминах, доступных «чайникам», гипотеза Римана утверждает существование системы в распределении простых чисел. Таким образом, значительно снижается стойкость криптографических ключей, от которых зависит безопасность онлайн-транзакций в сфере электронной коммерции.
Другие неразрешенные математические проблемы
Закончить статью стоит, посвятив несколько слов другим задачам тысячелетия. К их числу относятся:
- Равенство классов P и NP. Задача формулируется так: если положительный ответ на тот или иной вопрос проверяется за полиномиальное время, то верно ли, что и сам ответ на этот вопрос можно найти быстро?
- Гипотеза Ходжа. Простыми словами ее можно сформулировать так: для некоторых типов проективных алгебраических многообразий (пространств) циклы Ходжа являются комбинациями объектов, которые имеют геометрическую интерпретацию, т. е. алгебраических циклов.
- Гипотеза Пуанкаре. Это единственная из доказанных на данный момент задач тысячелетия. Согласно ей любой 3-мерный объект, обладающий конкретными свойствами 3-мерной сферы, обязан являться сферой с точностью до деформации.
- Утверждение квантовой теории Янга — Миллса. Требуется доказать, что квантовая теория, выдвинутая этими учеными для пространства R 4, существует и имеет 0-й дефект массы для любой простой калибровочной компактной группы G.
- Гипотеза Берча — Свиннертон-Дайера. Это еще одна проблема, имеющая отношение к криптографии. Она касается элиптических кривых.
- Проблема о существовании и гладкости решений уравнений Навье — Стокса.

Теперь вам известна гипотеза Римана. Простыми словами мы сформулировали и некоторые из других задач тысячелетия. То, что они будут решены либо будет доказано, что они не имеют решения, — это вопрос времени. Причем вряд ли этого придется ждать слишком долго, так как математика все больше использует вычислительные возможности компьютеров. Однако не все подвластно технике, и для решения научных проблем прежде всего требуется интуиция и творческий подход.


























