Что такое ромб? Известно, что это равносторонний четырехугольник, который также является параллелограммом. А если у ромба все углы равны, то эту фигуру уже можно назвать квадратом. А все противолежащие стороны ромба являются параллельными.
Что такое ромб
Ромб - это равносторонний параллелограмм. Само слово греческого происхождения, и означает "бубен". Это сегодня бубны круглой формы, раньше же их изготавливали в форме квадрата. Именно поэтому ромб имеет такое название. Также имеет наименование как геральдическая фигура. Обратимся к словарю Ушакова. Что же такое ромб? По сравнению с квадратом, это косоугольник с равными углами. А также квадрат - это частный случай ромба. Иногда даже говорят, что эти фигуры можно сравнить.

Также с ромбом связано изображение масти "бубна" на картах, которые используют в азартных играх. Также эту фигуру применяли для изображения на знаменах, флагах и различных гербах, но она встречается намного реже, чем другие геометрические конструкции. А сегодня ромб также используется для изображения баскетбольного поля. Что такое ромб, нам известно, но давайте рассмотрим свойства и признаки этой фигуры.
Свойства ромба
- Ромб представляется параллелограммом, все стороны которого лежат противоположно, являются равными и параллельными.
- Диагонали этой математической конструкции пересекаются лишь под прямым углом и делятся пополам в точке пересечения. То есть эти диагонали делят ромб на четыре абсолютно равных треугольника.
- Биссектрисами углов являются именно диагонали.
- Совокупность квадратов диагоналей равняется квадрату стороны, которая умножена на четыре.
- Вершинами прямоугольника являются середины четырех сторон этой конструкции под названием ромб.
- Диагонали фигуры перпендикулярны осями своей симметрии.
- Окружность с лежащим на пересечении центром можно вписать в любую фигуру под названием ромб.
- Что такое диагональ ромба? Это линия, которая соединяет его углы.
Признаки ромба
Мы узнали, что такое ромб, но помимо свойств у этой фигуры существуют еще и признаки. Любой параллелограмм будет являться ромбом, если будет выполнять хоть одно из приведенных ниже условий:
- Две смежные стороны ромба являются равными по отношению друг к другу.
- Диагонали этой математической конструкции могут пересекаться лишь под прямым углом и никак иначе.
- Одна из диагоналей обязательно делит пополам все ее углы, которые в ней содержаться.
- А если предположить, что нам не известно, что четырехугольник является параллелограммом, но известно, что стороны фигуры равны, тогда уверенно можно сказать: четырехугольник - это ромб.
- Это часть прямой, которая образует угол равный 90 градусам при пересечении противолежащей стороны.
- Что такое высота ромба? Это часть прямой, которая образует угол 90 градусов, пересекая противолежащую сторону.
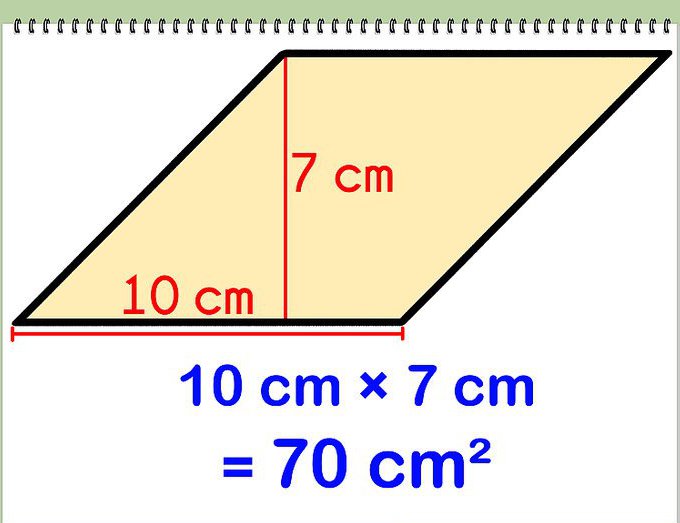
Площадь ромба
Нам известно, что такое ромб, каковы его свойства и признаки, но как же найти его площадь? Для того чтобы найти площадь ромба, следует поделить пополам произведения диагоналей этой фигуры. Так как ромб - это тот же параллелограмм, площадь такой математической конструкции равна произведению высоты на длину его сторон. Помимо этого, площадь фигуры можно найти при вычислении по формулам со смежными сторонами или же с радиусом вписанной окружности. Радиус вписанной окружности выражается через диагонали. Для того чтобы вычислить периметр ромба, следует умножить длину одной из четырех сторон на четыре.
А для того, чтобы изобразить эту фигуру в виде рисунка, нужно соблюдать нижеприведенные наставления. Ведь при построении этой фигуры у многих появляются трудности. Так вот, для того чтобы аккуратно изобразить ромб, следует для начала нарисовать первую диагональ, следом перпендикулярно вторую, в конце соединить края отрезков. Нужно очень внимательно и аккуратно рисовать эту фигуру, для того чтобы вместо ромба вы не нарисовали квадрат.

























