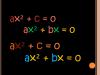Неполные квадратные уравнения и методы их решения с примерами

Неполные квадратные уравнения представляют собой частный случай равенств второго порядка. Необходимо уметь решать эти уравнения, поскольку они часто встречаются не только в математических, но и в физических задачах. Методам их решения посвящена эта статья.

Квадратные уравнения: полные и неполные

Перед тем как разбирать способы решения неполных квадратных уравнений, следует рассмотреть, что они собой представляют.

На рисунке ниже изображен общий вид равенств второго порядка, которые так называются из-за максимального значения степени переменной (она равна 2), содержащейся в них.

Где a, b и c - числа (коэффициенты). Неполное уравнение получается тогда, когда один из этих коэффициентов становится равным нулю (за исключением числа a, поскольку если оно занулится, то уравнение перестанет быть квадратным). Поскольку остается всего три возможные комбинации нулевых коэффициентов, то выделяют следующие типы неполных равенств второго порядка:

1. Только b=0. Тогда уравнение преобразуется к виду a*x² + c = 0. Оно называется чистым или простым неполным равенством квадратного типа.
2. Только c=0. Тогда получаем вид: a*x² + b*x = 0. Оно получило название смешенного неполного уравнения квадратного.
3. Наконец, если b=0 и c=0, то мы имеем выражение a*x²=0.

Последний вид неполного уравнения не рассматривается ни в одном математическом курсе, поскольку его решение является очевидным и единственно возможным: x=0.

Можно ли решать неполные уравнения с помощью формулы с дискриминантом?

Да, можно, поскольку этот способ является универсальным для любых выражений второго порядка. Однако неполные уравнения квадратные в 8 классе школы уже встречаются, и изучаться они начинают раньше, чем полные равенства этого типа, для которых уже приводится формула с дискриминантом. Кроме того, рассматриваемый вид равенств является достаточно простым, чтобы применять к ним универсальные формулы и производить ряд ненужных вычислений.

Рассмотрим простые и понятные способы решения неполных уравнений второго порядка.

Решение простого неполного уравнения

Схема его решения в общем случае представлена на рисунке ниже.

Объясним подробнее каждый отмеченный на ней шаг. Первым делом необходимо привести уравнение к виду, указанному в начале этой схемы. Условие задачи может быть так составлено, что исходное равенство будет содержать больше двух слагаемых. Все их необходимо упростить (умножить, сложить и вычесть) до вида чистого неполного равенства.

После этого свободный член c переносится в правую часть равенства и делится на коэффициент a. Для получения неизвестных x остается взять квадратный корень из отношения -c/a, при этом нужно не забывать и учитывать, что он может быть, как со знаком минус, так и с положительным знаком.

Что следует из представленной на рисунке формулы? Во-первых, корней чистого неполного квадратного равенства всегда 2-а, при этом по модулю они оба равны, а по знаку отличаются. Во-вторых, если числа c и a имеют один знак, то корни x будут мнимыми, если c и a разного знака, тогда получаются два действительных решения.

Решение смешанного неполного уравнения

Для решения квадратного уравнения, у которого c=0, следует проделать такой же первый шаг, как и в случае определения корней чистого неполного равенства, то есть привести его к виду с двумя слагаемыми: одно из них должно содержать x², а другое x. Затем, следует применить метод факторизации, то есть разложить левую часть равенства на множители. В отличие от полного уравнения это сделать очень просто, поскольку один из множителей всегда будет иксом. Сказанное выше можно записать в виде формулы:

x*(a*x+b) = 0.

Это равенство имеет решение, если каждый его множитель является нулем. Результат вычисления корней представлен на рисунке ниже.

Таким образом, корни этого типа неполного уравнения всегда будут действительными числами, причем один из них равен нулю. Знак второго корня определяется отношением ненулевых коэффициентов b/a.

Примеры математических задач

Теперь приведем наглядные примеры квадратных неполных уравнений с решением.

Пример 1. Найдите корни равенства 135-(2x + 3) (2x - 3) = 0. Раскрываем скобки, получаем: 135-4*x²+9=0. Заметим, что члены, содержащие x в первой степени, сократились. Выполняя перенос свободных членов в правую часть и деление их на -4, получаем: x² = 36. Откуда следуют два корня: 6 и -6.

Пример 2. 23*(x²-2)=34*x-46. Как и в первом случае, раскрываем скобки и переносим все слагаемые в левую часть. Имеем: 23*x²-46-34*x+46=0. Теперь сокращаем свободные члены и разлагаем сумму на множители, получаем: x*(23*x-34)=0. Откуда следует, что x=0 и x = 34/23≈1,47826.

Решение примеров показало, что алгоритм нахождения корней любого вида неполного уравнения второго порядка является достаточно простым, поэтому нет никакого смысла запоминать представленные на рисунках выше формулы.

Пример физической задачи

Многие школьники слышали от своего учителя физики о том, что Галилео Галилей в XVII веке проводил эксперименты по вычислению ускорения свободного падения, сбрасывая различные тела с башни в Пизе. Многим это покажется любопытным, но не существует ни одного исторического свидетельства, что такие эксперименты ученый действительно проводил. Однако в том же XVII веке их выполнил другой итальянец.

Джованни Риччоли - астроном и иезуит, который смог действительно вычислить ускорение падения свободного, сбрасывая глиняные шары с высоты башни Азинелли, находящейся в городе Болонье. Риччоли получил значение ускорения равное 9,6 м/с² (современная величина равна 9,81 м/с²). Зная это число, необходимо определить, сколько времени глиняный шар падал на землю, учитывая, что высота башни равна 97,6 метра.

Для решения задачи необходимо вспомнить, что путь при равноускоренном движении выражается формулой: l=v₀*t+g*t²/2. Поскольку в момент, когда Риччоли отпускал шар, скорость последнего была равна нулю, то член v₀*t = 0. Тогда мы приходим к уравнению: 97,6 = 9,6*t²/2. Откуда получаем, что t = 4,51 секунды (отрицательный корень был сознательно отброшен).