Объем треугольной призмы: формула общего типа и формула для правильной призмы

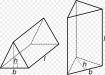
В физике треугольная призма, сделанная из стекла, часто используется для изучения спектра белого света, поскольку она способна разлагать его на отдельные составляющие. В данной статье рассмотрим формулу объема прямой треугольной призмы.

Что такое треугольная призма?

Перед тем как приводить формулу объема треугольной призмы, рассмотрим свойства этой фигуры.

Чтобы получить этот вид призмы, необходимо взять треугольник произвольной формы и параллельно самому себе перенести его на некоторое расстояние. Вершины треугольника в начальном и конечном положении следует соединить прямыми отрезками. Полученная объемная фигура называется треугольной призмой. Она состоит из пяти сторон. Две из них называются основаниями: они параллельны и равны друг другу. Основаниями рассматриваемой призмы являются треугольники. Три оставшиеся стороны - это параллелограммы.

Помимо сторон, рассматриваемая призма характеризуется шестью вершинами (по три для каждого основания) и девятью ребрами (6 ребер лежат в плоскостях оснований и 3 ребра образованы пересечением боковых сторон). Если боковые ребра перпендикулярны основаниям, то такая призма называется прямоугольной.

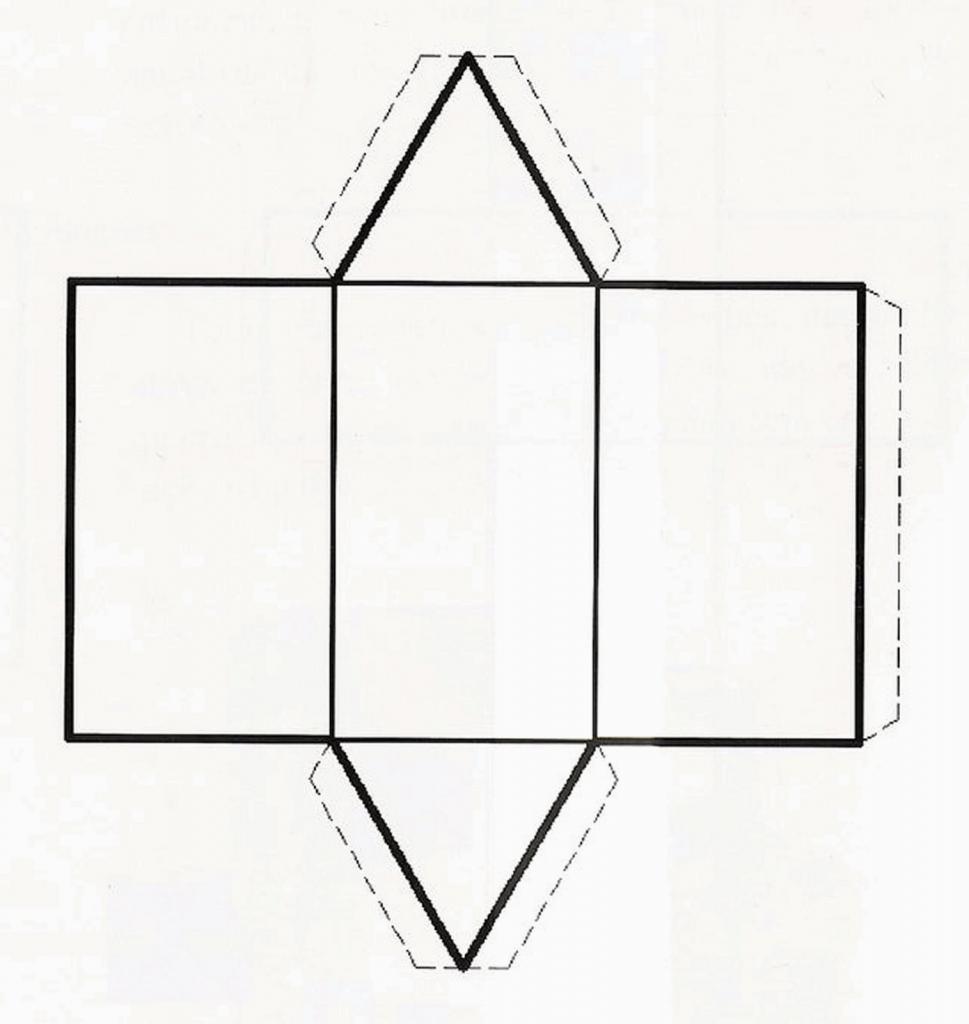
Отличие треугольной призмы от всех остальных фигур этого класса заключается в том, что она всегда является выпуклой (четырех-, пяти-, ..., n-угольные призмы могут также быть вогнутыми).

Правильная треугольная призма - это прямоугольная фигура, в основании которой лежит равносторонний треугольник.

Объем треугольной призмы общего типа

Как найти объем треугольной призмы? Формула в общем виде аналогична таковой для призмы любого вида. Она имеет такую математическую запись:

V = S_o * h

Здесь h - это высота фигуры, то есть расстояние между ее основаниями, S_o - площадь треугольника.

Величину S_o можно найти, если известны некоторые параметры для треугольника, например одна его сторона и два угла или две стороны и один угол. Площадь треугольника равна половине произведения его высоты на длину стороны, на которую опущена эта высота.

Что касается высоты h фигуры, то ее проще всего найти для прямоугольной призмы. В последнем случае h совпадает с длиной бокового ребра.

Объем правильной треугольной призмы

Общую формулу объема треугольной призмы, которая приведена в предыдущем разделе статьи, можно использовать для вычисления соответствующей величины для правильной треугольной призмы. Поскольку в ее основании лежит равносторонний треугольник, то его площадь равна:

S_o = √3/4 * a²

Эту формулу может получить каждый, если вспомнит, что в равностороннем треугольнике все углы равны друг другу и составляют 60^o. Здесь символ a - это длина стороны треугольника.

Высота h является длиной ребра. Она никак не связана с основанием правильной призмы и может принимать произвольные значения. В итоге формула объема треугольной призмы правильного вида выглядит так:

V = √3/4 * a² * h

Вычислив корень, можно переписать эту формулу так:

V = 0,433 * a² * h

Таким образом, чтобы найти объем правильной призмы с треугольным основанием, необходимо возвести в квадрат сторону основания, умножить эту величину на высоту и полученное значение умножить на 0,433.