Математическая статистика - это методология, которая позволяет принимать взвешенные решения среди неопределенных условий. Исследование способов сбора и систематизации данных, обработки итоговых результатов опытов и экспериментов с массовыми случайностями и обнаружение каких-либо закономерностей - это то, чем занимается данный раздел математики. Рассмотрим основные понятия математической статистики.
Разница с теорией вероятностей
Методы математической статистики тесно пересекаются с теорией вероятностей. Оба раздела математики занимаются исследованием многочисленных случайных явлений. Связывают две дисциплины между собой предельные теоремы. Однако существует большая разница между этими науками. Если теория вероятностей определяет на основе математической модели характеристики процесса в реальном мире, то математическая статистика делает наоборот - устанавливает свойства модели на основе наблюдаемой информации.

Этапы
Применение математической статистики может осуществляться только по отношению к случайным событиям или процессам, а точнее, к данным, полученным из наблюдения за ними. И происходит это в несколько этапов. Сначала данные экспериментов и опытов проходят определенную обработку. Их упорядочивают для наглядности и удобства анализа. Затем производится точная или приблизительная оценка требуемых параметров наблюдаемого случайного процесса. Ими могут быть:
- оценка вероятности того или иного события (вероятность его изначально неизвестна);
- изучение поведения неопределенной функции распределения;
- оценка математического ожидания;
- оценка дисперсии
- и т. д.
В третий этап можно выделить проверку каких-либо гипотез, поставленных до проведения анализа, т. е. получение ответа на вопрос о том, насколько результаты экспериментов соответствуют теоретическим выкладкам. По факту, это основной этап математической статистики. Примером может быть рассмотрение вопроса о том, находится ли поведение наблюдаемого случайного процесса в пределах нормального закона распределения.
Генеральная совокупность
В основные понятия математической статистики входят генеральная и выборочная совокупности. Данная дисциплина занимается изучением множества некоторых объектов касательно какого-либо свойства. В качестве примера можно привести работу таксиста. Рассмотрим эти случайные величины:
- загруженность или количество клиентов: в сутки, до обеда, после обеда, ...;
- среднее время поездки;
- количество поступающих заявок или их привязанность к районам города и многое другое.
Стоит также отметить, что можно исследовать совокупность подобных случайных процессов, которая также будет представлять собой случайную величину, над которой можно проводить наблюдения.

Итак, в методах математической статистики все множество исследуемых объектов или результатов всевозможных наблюдений, которые проводятся в одинаковых условиях над взятым объектом, называется генеральной совокупностью. Иными словами, математически более строго, это случайная величина, которая определена в пространстве элементарных событий, с обозначенным в нем классом подмножеств, элементы которого обладают известной вероятностью.
Выборочная совокупность
Бывают случаи, когда невозможно или нецелесообразно по каким-то причинам (стоимость, затраты времени) провести сплошное исследование для изучения каждого объекта. Например, открывать каждую банку запечатанного варенья для контроля его качества - сомнительное решение, а попытка оценить траекторию каждой молекулы воздуха в кубическом метре - невыполнима. В таких случаях используют способ выборочного наблюдения: из генеральной совокупности производится выбор (как правило, случайным образом) некоторого количества объектов, и их подвергают их анализу.
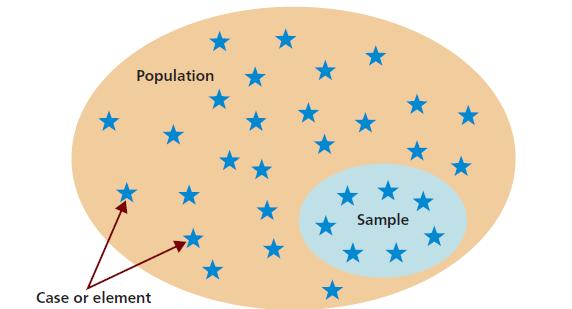
Эти понятия могут казаться сложными поначалу. Поэтому, чтобы наиболее полно понять тему, нужно изучать учебник В. Е. Гмурмана "Теория вероятностей и математическая статистика". Таким образом, выборочная совокупность или выборка - это ряд объектов, выбранных случайным образом из генерального множества. Говоря строгим математическим языком, это последовательность независимых, равномерно распределенных случайных величин, для каждой из которых распределение совпадает с тем, которое обозначено для генеральной случайной величины.
Основные понятия
Рассмотрим вкратце ряд других основных понятий математической статистики. Число объектов в генеральной совокупности или выборке называется объемом. Значения выборки, которые получают в ходе эксперимента, называются реализацией выборки. Чтобы оценка генеральной совокупности на основе выборочной была достоверной, важно иметь так называемую представительную или репрезентативную выборку. Это значит, что выборка должна в полном объеме представлять генеральную совокупность. Добиться этого можно только в том случае, когда все элементы генеральной совокупности имеют равную вероятность оказаться в выборке.

Выборки различают с возвращением и без возвращения. В первом случае в содержимом выборки повторный элемент возвращается в генеральное множество, во втором - нет. Обычно на практике применяется выборка без возвращений. Следует также отметить, что объем генеральной совокупности всегда значительно превосходит объем выборки. Существует множество вариантов процесса выборки:
- простой - элементы выбираются случайным образом по одному;
- типизированный - генеральная совокупность разделяется на типы, и из каждого производится выбор; примером может послужить опрос жителей: мужчины и женщины раздельно;
- механический - например, выбрать каждый 10-й элемент;
- серийный - выбор производится сериями элементов.
Статистическое распределение
Согласно Гмурману, теория вероятностей и математическая статистика являются крайне важными дисциплинами в научном мире, особенно в практической его части. Рассмотрим статистическое распределение выборки.
Пусть у нас имеется группа студентов, в которой было проведено тестирование по математике. В итоге у нас есть совокупность оценок: 5, 3, 1, 4, 3, 4, 2, 5, 4, 4, 5 - это наш первичный статистический материал.
Первым делом нам нужно его упорядочить, или провести операцию ранжирования: 1, 2, 3, 3, 4, 4, 4, 4, 5, 5, 5 - и получить, таким образом, вариационный ряд. Количество повторений каждой из оценок при этом называется частотой оценки, а их отношение к объему выборки - относительной частотой. Составим таблицу статистического распределения выборки, или просто статистический ряд:
| ai | 1 | 2 | 3 | 4 | 5 |
| pi | 1 | 1 | 2 | 4 | 3 |
или
| ai | 1 | 2 | 3 | 4 | 5 |
| pi* | 1/11 | 1/11 | 2/11 | 4/11 | 3/11 |
Пусть у нас имеется случайная величина, над которой мы будем проводить серию экспериментов и смотреть, какое значение принимает эта величина. Допустим, она приняла значение a1 - m1 раз; a2 - m2 раз и т.д. Объемом данной выборки будет m1 + ... + mk = m. Множество ai, где i меняется от 1 до k, представляет собой статистический ряд.
Интервальное распределение
В книге В. Е. Гмурмана "Теория вероятностей и математическая статистика" также представлен интервальный статистический ряд. Его составление возможно, когда значение исследуемого признака непрерывно в определенном интервале, и число значений велико. Рассмотрим группу студентов, а точнее, их рост: 163, 180, 185, 172, 161, 171, 189, 157, 165, 174, 180, 181, 175, 182, 167, 159, 173, 171, 164, 179, 160, 180, 166, 178, 156, 180, 189, 173, 174, 175 - всего 30 студентов. Очевидно, что рост человека - это непрерывная величина. Нам нужно определить шаг интервала. Для этого используется формула Стерджеса.
| h= | max - min | = | 190 - 156 | = | 33 | = | 5,59 |
| 1+log2m | 1+log230 | 5,9 |
Таким образом, за размер интервала можно принять величину 6. Также следует сказать, что значение 1+log2m - это формула для определения количества интервалов (разумеется, с округлением). Таким образом, получается по формулам 6 интервалов, каждый из которых имеет размер 6. И первым значением начального интервала будет число, определяемое по формуле: min - h/2 = 156 - 6/2 = 153. Составим таблицу, которая будет содержать интервалы и число студентов, рост которых попал в определенный интервал.
| H | [153; 159) | [159; 165) | [165; 171) | [171; 177) | [177; 183) | [183; 189) |
| P | 2 | 5 | 3 | 9 | 8 | 3 |
| P* | 0,06 | 0,17 | 0,1 | 0,3 | 0,27 | 0,1 |
Разумеется, это далеко не все, ибо в математической статистике формул куда больше. Мы рассмотрели лишь некоторые базовые понятия.
График распределения
В основные понятия математической статистики также входит графическое представление распределения, которое отличается наглядностью. Существует два вида графиков: полигон и гистограмма. Первый используется для дискретного статистического ряда. А для непрерывного распределения, соответственно, второй.


























