Полином, или многочлен - одна из базовых алгебраических структур, которая встречается в школьной и высшей математике. Изучение полинома - важнейшая тема в курсе алгебры, поскольку с одной стороны многочлены достаточно просты по сравнению с другими типами функций, с другой - широко применяются в решении задач математического анализа. Итак, что такое полином?
Определение
Определение термину полином можно дать через понятие монома, или одночлена.
Мономом называют выражение вида сх1i1x2i2...xnin. Здесь с - константа, x1, x2, ... xn - переменные, i1, i2, ... in - показатели степеней переменных. Тогда полином - любая конечная сумма мономов.
Чтобы понять, что такое полином, можно посмотреть на конкретные примеры.
Квадратный трехчлен, подробно рассматриваемый в курсе математики 8-го класса, - это полином: ax2+bx+c.
Многочлен с двумя переменными может выглядеть так: х2-ху+у2. Такой полином называют еще неполным квадратом разности х и у.
Классификации полиномов
По степени полинома
Для каждого монома в составе многочлена находят сумму показателей степени i1+i2+...+in. Наибольшую из сумм называют показателем степени полинома, а одночлен, соответствующий этой сумме, - старшим членом.
Кстати, любую константу можно считать многочленом степени ноль.
Приведенные и неприведенные полиномы
Если у старшего члена коэффициент с равен 1, то многочлен приведен, иначе - нет.
Например, выражение х2+2х+1 - приведенный полином, а 2х2+2х+1 - неприведенный.
Однородные и неоднородные полиномы
Если степени всех членов полинома равны, то говорят, что такой полином однороден. Все остальные полиномы считаются неоднородными.
Однородные многочлены: х2-ху+у2, xyz+х3+у3. Неоднородные: х+1, х2+у.
Существуют специальные названия для полинома из двух и трех членов: бином и трехчлен соответственно.
В отдельную категорию выделяют многочлены одной переменной.
Применение полинома одной переменной
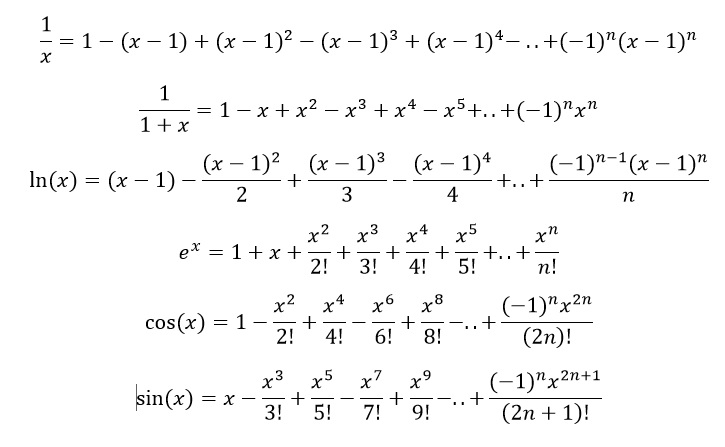
Многочлены одной переменной хорошо приближают непрерывные функции различной сложности от одного аргумента.
Дело в том, что такие полиномы можно рассматривать как частичные суммы степенного ряда, а непрерывную функцию можно представить в виде ряда со сколь угодно малой погрешностью. Ряды разложения функции называют рядами Тейлора, а их частичные суммы в виде полиномов - многочленами Тейлора.
Изучить графически поведение функции, аппроксимировав ее некоторым многочленом, зачастую легче, чем исследовать ту же функцию непосредственно или с помощью ряда.
Легко искать производные многочленов. Для нахождения корней у полиномов 4-й степени и ниже существуют готовые формулы, а для работы с более высокими степенями используются приближенные алгоритмы высокой точности.
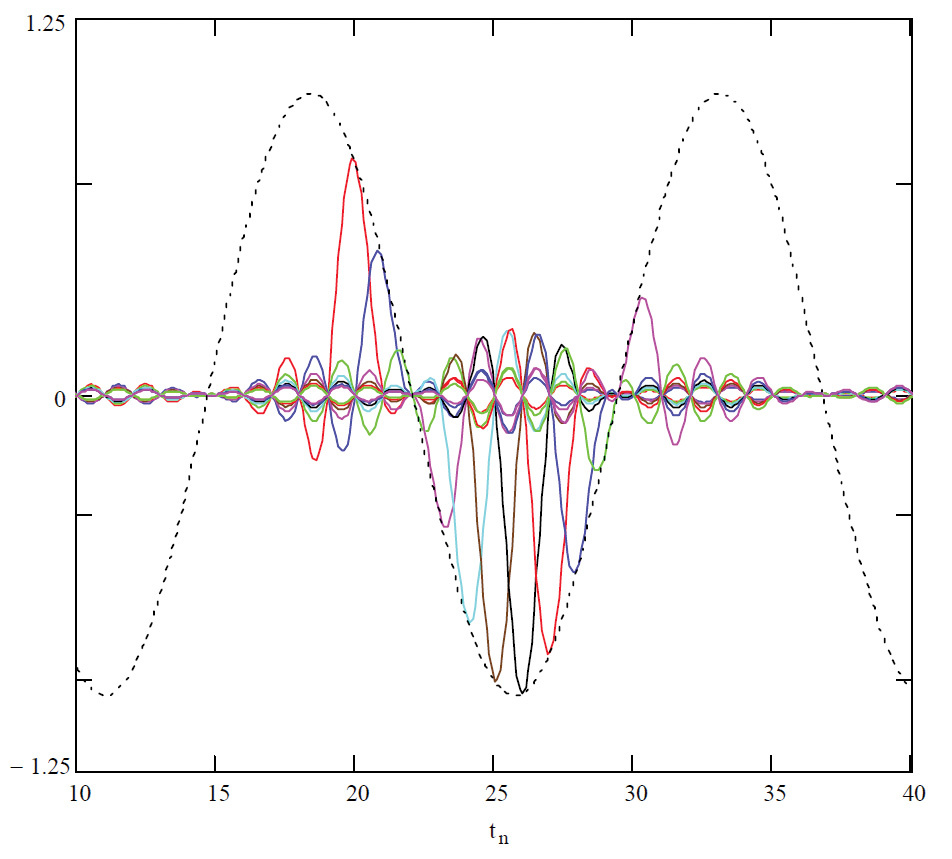
Существует и обобщение описанных многочленов для функций многих переменных.
Бином Ньютона
Знаменитыми полиномами являются полиномы Ньютона, выведенные ученым для нахождения коэффициентов выражения (х+у)n.
Достаточно посмотреть на несколько первых степеней разложения бинома, чтобы убедиться в нетривиальности формулы:
(х+у)2=х2+2ху+у2;
(х+у)3=х3+3х2у+3ху2+у3;
(х+у)4=х4+4х3у+6х2у2+4ху3+у4;
(х+у)5=х5+5х4у+10х3у2+10х2у3+5ху4+у5.
Для каждого коэффициента существует выражение, позволяющее его вычислить. Однако запоминать громоздкие формулы и каждый раз производить необходимые арифметические операции было бы крайне неудобно для тех математиков, которым часто требуются подобные разложения. Им значительно облегчил жизнь треугольник Паскаля.
Фигура строится по следующему принципу. В вершине треугольника пишется 1, а в каждой следующей строке становится на одну цифру больше, по краям ставят 1, а середина строчки заполняется суммами двух соседних чисел из предыдущей.
При взгляде на иллюстрацию все становится понятно.
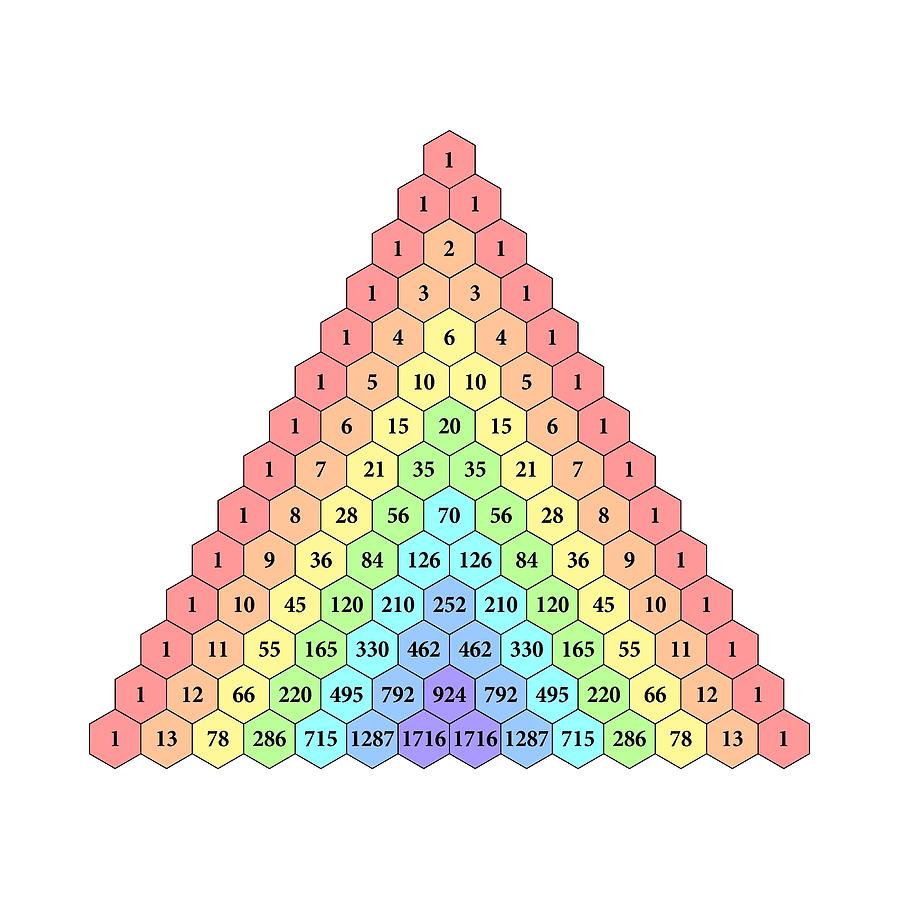
Разумеется, приведенными примерами, наиболее широко известными, применение многочленов в математике не ограничивается.
























