Обратные тригонометрические функции традиционно вызывают сложности у школьников. Умение вычислять арктангенс числа может потребоваться в задачах ЕГЭ по планиметрии и стереометрии. Для успешного решения уравнения и задачи с параметром необходимо иметь представление о свойствах функции арктангенса.
Определение
Арктангенсом числа х называется такое число у, тангенс которого равен х. Это есть математическое определение.
Функция арктангенса записывается как y = arctg x.
В более общем виде: y = Carctg (kx + a).
Вычисление
Для понимания того, как устроена обратная тригонометрическая функция арктангенса, нужно для начала вспомнить, как определяют значение тангенса числа. Рассмотрим подробнее.
Тангенс х - это отношение синуса х к косинусу х. Если известна хотя бы одна из этих двух величин, то модуль второй может быть получен из основного тригонометрического тождества:
sin2 x + cos2 x = 1.
Правда, для раскрытия модуля потребуется проведение оценки.
Если же известно само число, а не его тригонометрические характеристики, то в большинстве случаев нужно примерно оценить тангенс числа, обратившись к таблице Брадиса.
Исключения составляют так называемые стандартные значения.
Они представлены в следующей таблице:
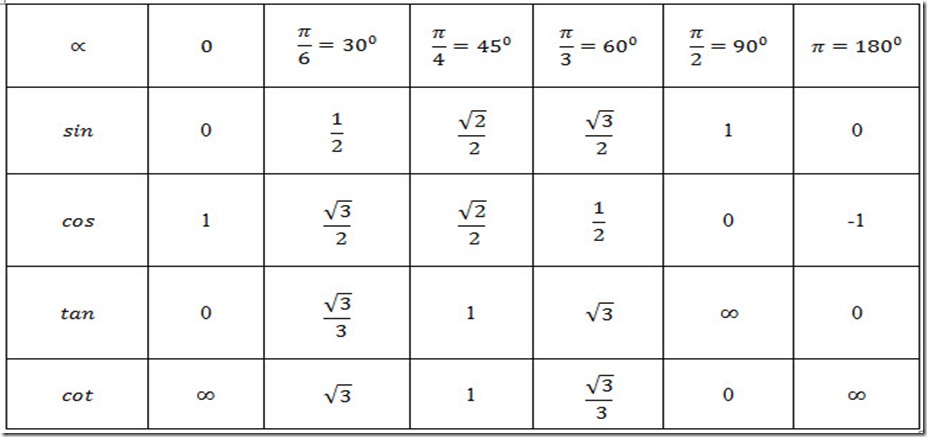
Кроме перечисленных выше, стандартными можно считать любые значения, полученные из данных добавлением числа вида ½πк (к - любое целое число, π=3,14).
Ровно то же самое верно и для арктангенса: чаще всего приближенное значение можно посмотреть по таблице, а точно известны лишь несколько значений:
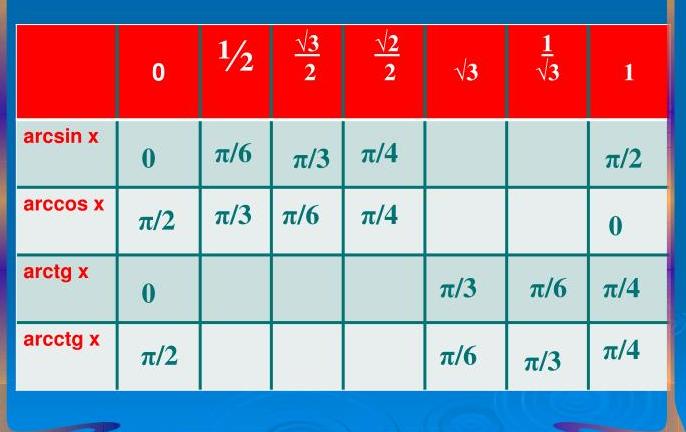
На практике при решении задач школьной математики принято давать ответ в виде выражения, содержащего арктангенс, а не его приблизительной оценки. Например, arctg 6, arctg (-¼).
Построение графика
Поскольку тангенс может принимать любые значения, область определения функции арктангенса - вся числовая прямая. Поясним подробнее.
Один и тот же тангенс соответствует бесконечному числу аргументов. Например, нулю равен не только тангенс нуля, но и тангенс любого числа вида π к, где к - целое число. Поэтому математики условились выбирать для арктангенса значения из промежутка от -½ π до ½ π. Это нужно понимать так. Область значений функции арктангенса - интервал (-½ π; ½ π). Концы промежутка не включаются, так как тангенс -½п и ½п не существует.
На указанном интервале тангенс непрерывно возрастает. Значит, обратная функция арктангенса тоже является непрерывно возрастающей на всей числовой прямой, но ограниченной сверху и снизу. Вследствие этого она имеет две горизонтальные асимптоты: y = -½ π и y = ½ π.
В этом случае tg 0 = 0, других точек пересечения с осью абсцисс, кроме (0;0), график не может иметь в силу возрастания.
Как следует из четности функции тангенса, арктангенс имеет аналогичное свойство.
Для построения графика следует взять несколько точек из числа стандартных значений:
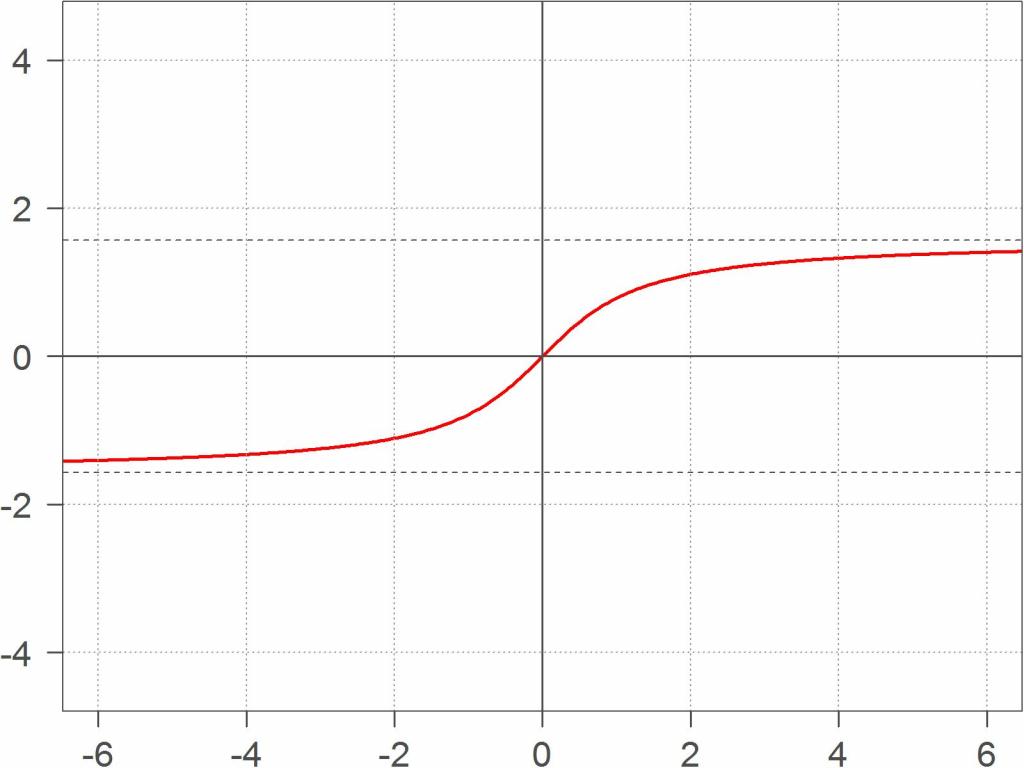
Производная функции y = arctg х в любой точке вычисляется по формуле:
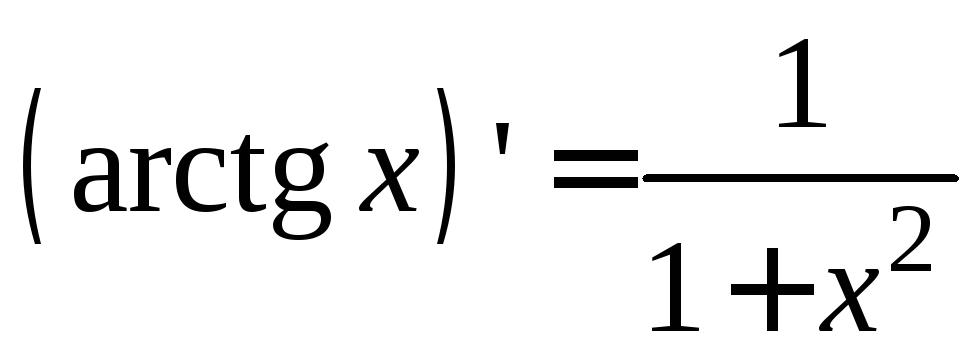
Заметим, что его производная всюду положительна. Это согласуется со сделанным ранее выводом о непрерывном возрастании функции.
Вторая производная арктангенса обращается в 0 в точке 0, отрицательна при положительных значениях аргумента и наоборот.
Это означает, что график функции арктангенса имеет точку перегиба в нуле и является выпуклым вниз на промежутке (-∞; 0] и выпуклым вверх на промежутке [0; +∞).

























