Термодинамика как самостоятельный раздел физической науки возникла в первой половине XIX века. Грянул век машин. Промышленная революция требовала изучить и осмыслить процессы, связанные с функционированием тепловых двигателей. На заре машинной эры изобретатели-одиночки могли себе позволить использовать лишь интуицию и «метод тыка». Не было общественного заказа на открытия и изобретения, никому даже в голову не могло прийти, что они могут быть полезны. Но когда тепловые (а немного позже и электрические) машины стали основой производства, ситуация изменилась. Ученые наконец постепенно разобрались с терминологической путаницей, царившей до середины XIX века, определившись, что называть энергией, что силой, что - импульсом.
Что постулирует термодинамика
Начнем с общеизвестных сведений. Классическая термодинамика основана на нескольких постулатах (началах), последовательно вводившихся на протяжении XIX века. То есть эти положения не являются доказуемыми в ее рамках. Они были сформулированы в результате обобщения эмпирических данных.
Первое начало – это приложение закона сохранения энергии к описанию поведения макроскопических систем (состоящих из большого числа частиц). Коротко его можно сформулировать так: запас внутренней энергии изолированной термодинамической системы всегда остается постоянным.
Смысл второго начала термодинамики состоит в определении направления, в котором протекают процессы в таких системах.
Третье начало позволяет точно определить такую величину, как энтропия. Рассмотрим ее подробнее.
Понятие энтропии
Формулировка второго начала термодинамики была предложена в 1850 году Рудольфом Клаузиусом: «Невозможен самопроизвольный переход теплоты от менее нагретого тела к более нагретому». При этом Клаузиус подчеркивал заслугу Сади Карно, еще в 1824 году установившего, что доля энергии, которая может быть превращена в работу тепловой машины, зависит только от разности температур нагревателя и холодильника.

При дальнейшей разработке второго начала термодинамики Клаузиус вводит понятие энтропии - меры количества энергии, которая необратимо переходит в форму, непригодную для обращения в работу. Клаузиус выразил эту величину формулой dS = dQ/T, где dS, определяющей изменение энтропии. Здесь:
dQ - изменение теплоты;
T – абсолютная температура (та самая, которая измеряется в кельвинах).
Простой пример: потрогайте капот вашего автомобиля при включенном двигателе. Он явно теплее окружающей среды. Но ведь двигатель автомобиля предназначен не для того, чтобы нагревать капот или воду в радиаторе. Преобразуя химическую энергию бензина в тепловую, а затем в механическую, он совершает полезную работу – вращает вал. Но большая часть вырабатываемого тепла теряется, так как никакой полезной работы из него извлечь нельзя, а то, что вылетает из выхлопной трубы, уже никоим образом бензином не является. При этом тепловая энергия теряется, но не исчезает, а рассеивается (диссипирует). Горячий капот, конечно, остывает, а каждый цикл цилиндров в двигателе снова добавляет ему теплоту. Таким образом система стремится достичь термодинамического равновесия.
Особенности энтропии
Клаузиус вывел общий принцип для второго начала термодинамики в формуле dS ≥ 0. Физический смысл ее можно определить, как "неубывание" энтропии: в обратимых процессах она не меняется, в необратимых - возрастает.
Следует заметить, что все реальные процессы необратимы. Термин «неубывание» отражает лишь тот факт, что в рассмотрение явления включен также теоретически возможный идеализированный вариант. То есть количество недоступной энергии в любом самопроизвольном процессе увеличивается.
Возможность достижения абсолютного нуля
Макс Планк внес серьезный вклад в разработку термодинамики. Помимо работы над статистической интерпретацией второго начала, он принял деятельное участие в постулировании третьего начала термодинамики. Первая формулировка принадлежит Вальтеру Нернсту и относится к 1906 году. Теорема Нернста рассматривает поведение равновесной системы при температуре, стремящейся к абсолютному нулю. Первое и второе начала термодинамики не дают возможности выяснить, какова будет энтропия в данных условиях.

При T = 0 K энергия равна нулю, частицы системы прекращают хаотические тепловые движения и образуют упорядоченную структуру, кристалл с термодинамической вероятностью, равной единице. Значит, энтропия тоже обращается в ноль (ниже мы узнаем, почему так происходит). В реальности она даже делает это несколько раньше, из чего следует, что охлаждение любой термодинамической системы, любого тела до абсолютного нуля невозможно. Температура будет сколь угодно приближаться к этой точке, но не достигнет ее.
Перпетуум-мобиле: нельзя, даже если очень хочется
Клаузиус обобщил и сформулировал первое и второе начала термодинамики таким образом: полная энергия любой замкнутой системы всегда остается постоянной, а полная энтропия возрастает с течением времени.
Первая часть этого утверждения налагает запрет на вечный двигатель первого рода – устройство, совершающее работу без притока энергии из внешнего источника. Вторая часть запрещает и вечный двигатель второго рода. Такая машина переводила бы энергию системы в работу без энтропийной компенсации, не нарушая закона сохранения. Можно было бы откачивать тепло из равновесной системы, например, жарить яичницу или лить сталь за счет энергии теплового движения молекул воды, охлаждая ее при этом.
Второе и третье начала термодинамики запрещают вечный двигатель второго рода.
Увы, у природы ничего нельзя получить не только даром, приходится еще и комиссию выплачивать.
«Тепловая смерть»
Мало найдется в науке понятий, которые вызывали столько неоднозначных эмоций не только у широкой публики, но и в среде самих ученых, сколько пришлось на долю энтропии. Физики, и в первую очередь сам Клаузиус, практически сразу экстраполировали закон неубывания сначала на Землю, а затем и на всю Вселенную (почему бы и нет, ведь ее тоже можно считать термодинамической системой). В итоге физическая величина, важный элемент расчетов во многих технических приложениях, стала восприниматься как воплощение некоего вселенского Зла, уничтожающего светлый и добрый мир.
В среде ученых есть и такие мнения: поскольку, согласно второму началу термодинамики, энтропия необратимо растет, рано или поздно вся энергия Вселенной деградирует в рассеянную форму, и наступит «тепловая смерть». Чему тут радоваться? Клаузиус, например, несколько лет не решался на публикацию своих выводов. Разумеется, гипотеза «тепловой смерти» немедленно вызвала множество возражений. Серьезные сомнения в ее правильности есть и сейчас.
Демон-сортировщик
В 1867 году Джеймс Максвелл, один из авторов молекулярно-кинетической теории газов, в очень наглядном (хоть и вымышленном) эксперименте продемонстрировал кажущуюся парадоксальность второго начала термодинамики. Кратко опыт можно изложить следующим образом.
Пусть имеется сосуд с газом. Молекулы в нем движутся хаотически, скорости их несколько различаются, но средняя кинетическая энергия одинакова по всему сосуду. Теперь разделим сосуд перегородкой на две изолированные части. Средняя скорость молекул в обеих половинках сосуда останется одинаковой. Перегородку сторожит крохотный демон, который позволяет более быстрым, «горячим» молекулам проникать в одну часть, а более медленным «холодным» - в другую. В результате в первой половинке газ нагреется, во второй – охладится, то есть из состояния термодинамического равновесия система перейдет к разности температурных потенциалов, что означает уменьшение энтропии.
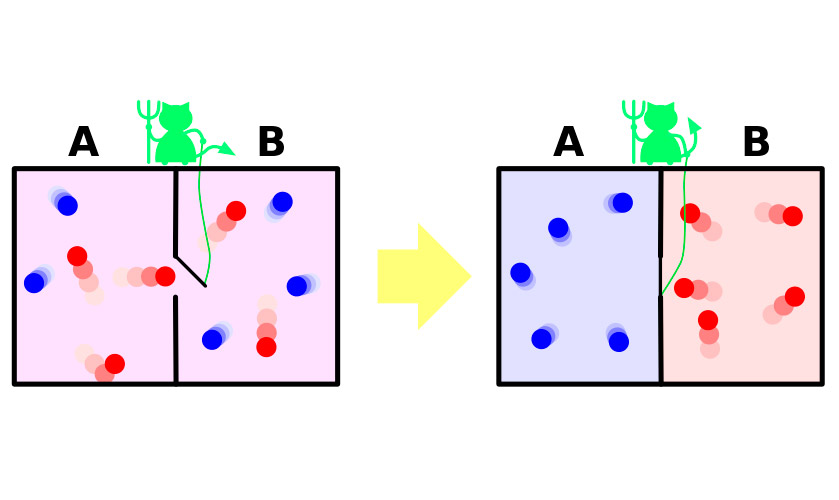
Вся проблема в том, что в эксперименте система совершает этот переход не самопроизвольно. Она получает извне энергию, за счет которой открывается и закрывается перегородка, либо система с необходимостью включает в себя демона, затрачивающего свою энергию на исполнение обязанностей привратника. Увеличение энтропии демона с избытком покроет уменьшение ее в газе.
Недисциплинированные молекулы
Возьмем стакан с водой и оставим его на столе. Наблюдать за стаканом не обязательно, достаточно через некоторое время вернуться и проверить состояние воды в нем. Мы увидим, что ее количество уменьшилось. Если же оставить стакан надолго, в нем вообще не обнаружится воды, так как вся она испарится. В самом начале процесса все молекулы воды находились в некой ограниченной стенками стакана области пространства. В конце эксперимента они разлетелись по всей комнате. В объеме комнаты у молекул гораздо больше возможностей менять свое местоположение без всяких последствий для состояния системы. Мы никак не сможем собрать их в спаянный "коллектив" и загнать обратно в стакан, чтобы с пользой для здоровья выпить воду.

Это значит, что система эволюционировала к состоянию с более высокой энтропией. Исходя из второго начала термодинамики, энтропия, или процесс рассеивания частиц системы (в данном случае молекул воды) необратим. Почему это так?
Клаузиус не ответил на этот вопрос, да и никто другой не смог этого сделать до Людвига Больцмана.
Макро и микросостояния
В 1872 году этот ученый ввел в науку статистическое толкование второго начала термодинамики. Ведь макроскопические системы, с которыми имеет дело термодинамика, образованы большим количеством элементов, поведение которых подчиняется статистическим законам.
Вернемся к молекулам воды. Хаотически летая по комнате, они могут занимать разные положения, иметь некоторые различия в скоростях (молекулы постоянно сталкиваются друг с другом и с другими частицами в воздухе). Каждый вариант состояния системы молекул называется микросостоянием, и таких вариантов огромное количество. При реализации подавляющего большинства вариантов макросостояние системы не изменится никак.
Ничто не запрещено, но кое-что крайне маловероятно
Знаменитое соотношение S = k lnW связывает число возможных способов, которым можно выразить определенное макросостояние термодинамической системы (W), с ее энтропией S. Величину W называют термодинамической вероятностью. Окончательный вид этой формуле придал Макс Планк. Коэффициент k – чрезвычайно малую величину (1,38×10−23 Дж/К), характеризующую связь между энергией и температурой, Планк назвал постоянной Больцмана в честь ученого, который первым предложил статистическое толкование второго начала термодинамики.

Ясно, что W – всегда натуральное число 1, 2, 3,…N (не бывает дробного количества способов). Тогда логарифм W, а следовательно, и энтропия, не могут быть отрицательными. При единственно возможном для системы микросостоянии энтропия становится равной нулю. Если вернуться к нашему стакану, этот постулат можно представить так: молекулы воды, беспорядочно снующие по комнате, вернулись обратно в стакан. При этом каждая в точности повторила свой путь и заняла в стакане то же место, в каком пребывала перед вылетом. Ничто не запрещает реализацию этого варианта, при котором энтропия равна нулю. Только ждать осуществления такой исчезающе малой вероятности не стоит. Это один из примеров того, что можно осуществить лишь теоретически.
Все смешалось в доме…
Итак, молекулы хаотически летают по комнате разными способами. Нет никакой закономерности в их расположении, нет порядка в системе, как ни меняй варианты микросостояний, не прослеживается никакой внятной структуры. В стакане было то же самое, но из-за ограниченности пространства молекулы меняли свое положение не так активно.
Хаотическое, неупорядоченное состояние системы как наиболее вероятное соответствует ее максимальной энтропии. Вода в стакане являет пример более низкоэнтропийного состояния. Переход к нему из равномерно распределенного по комнате хаоса практически неосуществим.
Приведем более понятный для всех нас пример - уборка беспорядка в доме. Чтобы все расставить по местам, нам тоже приходится затрачивать энергию. В процессе этой работы нам становится жарко (то есть мы не мерзнем). Оказывается, энтропия может принести пользу. Это так и есть. Можно сказать даже больше: энтропия, а через нее второе начало термодинамики (наряду с энергией) управляют Вселенной. Взглянем еще раз на обратимые процессы. Так выглядел бы мир, не будь энтропии: никакого развития, никаких галактик, звезд, планет. Никакой жизни...
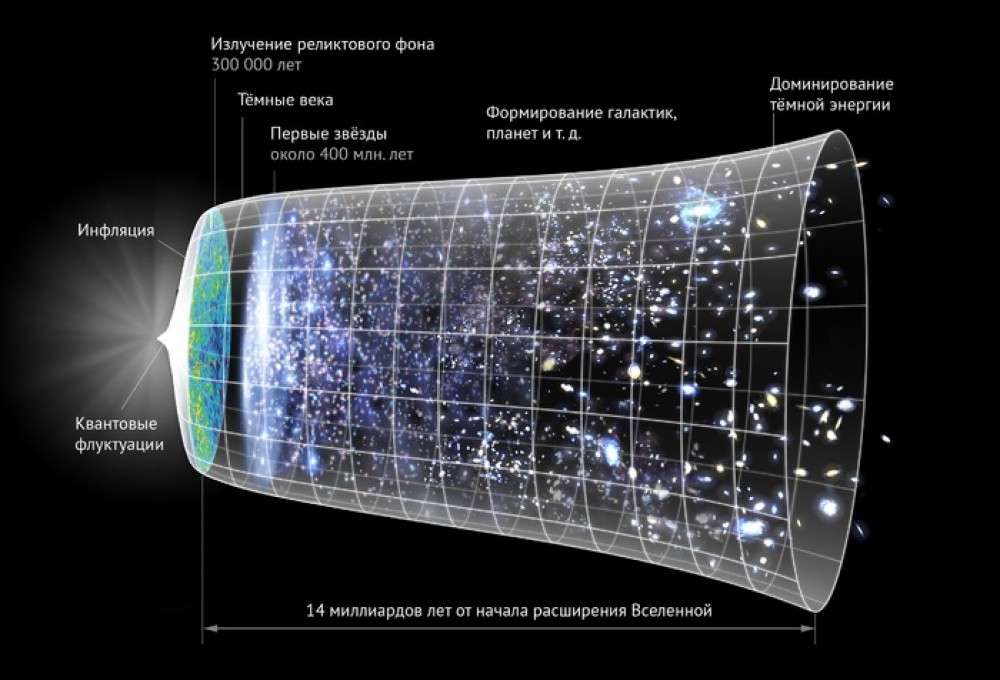
Еще немного информации о «тепловой смерти». Есть хорошие новости. Поскольку, согласно статистической теории, «запрещенные» процессы на самом деле являются маловероятными, в термодинамически равновесной системе возникают флуктуации – спонтанные нарушения второго начала термодинамики. Они могут быть сколь угодно большими. При включении гравитации в термодинамическую систему распределение частиц уже не будет хаотически-равномерным, а состояние максимальной энтропии не будет достигнуто. Кроме того, Вселенная не является неизменной, постоянной, стационарной. Следовательно, сама постановка вопроса о «тепловой смерти» лишена смысла.



























