Любое перемещение тела в пространстве, которое приводит к изменению его полной энергии, связано с работой. В данной статье рассмотрим, что это за величина, в чем измеряется механическая работа, и как она обозначается, а также решим интересную задачу по этой теме.
Работа как физическая величина
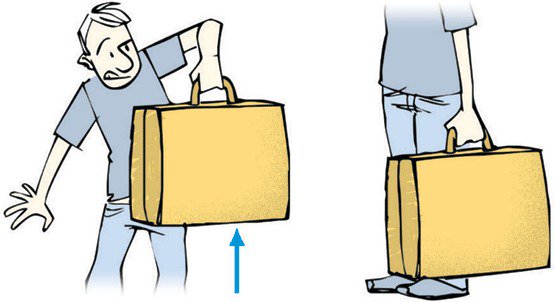
Перед тем как ответить на вопрос, в чем измеряется механическая работа, познакомимся с этой величиной. Согласно определению, работа представляет собой скалярное произведение силы на вектор перемещения тела, который эта сила вызвала. Математически можно записать следующее равенство:
A = (F¯*S¯).
Круглые скобки указывают на скалярное произведение. Учитывая его свойства, в явном виде эта формула перепишется так:
A = F*S*cos(α).
Где α является углом между векторами силы и перемещения.
Из записанных выражений следует, что работа измеряется в Ньютонах на метр (Н*м). Как известно, эта величина называется джоулем (Дж). То есть в физике работа механическая в единицах работы Джоулях измеряется. Одному Джоулю соответствует такая работа, при которой сила в один Ньютон, действуя параллельно перемещению тела, приводит к изменению его положения в пространстве на один метр.
Что касается обозначения механической работы в физике, то следует отметить, что для этого чаще всего пользуются буквой A (от нем. ardeit - труд, работа). В англоязычной литературе можно встретить обозначение этой величины латинской буквой W. В русскоязычной литературе эта буква зарезервирована для обозначения мощности.
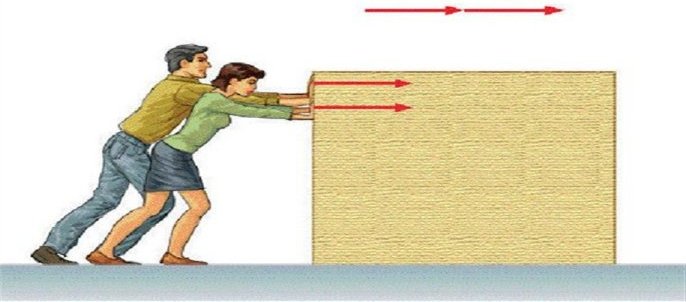
Работа и энергия
Разбирая вопрос, в чем измеряется механическая работа, мы увидели, что ее единицы совпадают с таковыми для энергии. Это совпадение не является случайным. Дело в том, что рассматриваемая физическая величина является одним из способов проявления энергии в природе. Любое перемещение тел в силовых полях или в их отсутствии требует энергетических затрат. Последние идут на изменение кинетической и потенциальной энергии тел. Процесс этого изменения характеризуется выполняемой работой.
Энергия является фундаментальной характеристикой тел. Она сохраняется в изолированных системах, она может преобразовываться в механическую, химическую, тепловую, электрическую и другие формы. Работа же является лишь механическим проявлением энергетических процессов.
Работа в газах
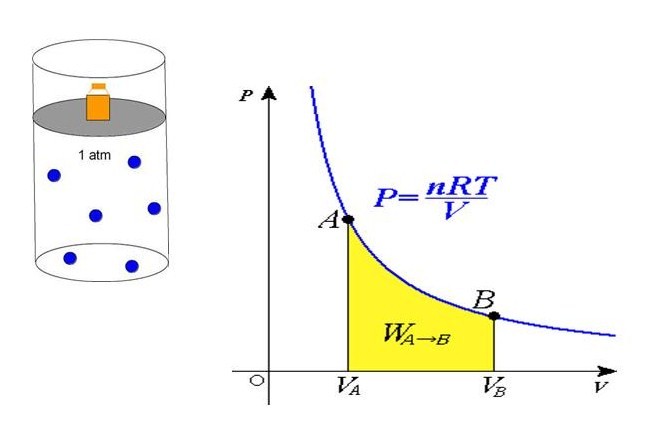
Записанное выше выражение для работы является базовым. Тем не менее, для решения практических задач из разных областей физики эта формула может быть непригодна, поэтому пользуются другими выражениями, полученными на ее основе. Одним из таких случаев является совершаемая газом работа. Ее удобно рассчитывать по следующей формуле:
A = ∫V(P*dV).
Здесь P - это давление в газе, V - его объем. Зная, в чем измеряется механическая работа, легко доказать справедливость интегрального выражения, действительно:
Па*м3 = Н/м2*м3 = Н*м = Дж.
В общем случае давление - это функция объема, поэтому подынтегральное выражение может принимать произвольный вид. В случае изобарного процесса расширение или сжатие газа происходит при постоянном давлении. В этом случае работа газа равна простому произведению величины P на изменение его объема.
Работа при вращении тела вокруг оси

Движение вращения широко распространено в природе и в технике. Характеризуется оно понятиями моментов (силы, импульса и инерции). Чтобы определить работу внешних сил, которые заставили тело или систему вращаться вокруг некоторой оси, необходимо сначала рассчитать момент силы. Вычисляется он так:
M = F*d.
Где d - это расстояние от вектора силы до оси вращения, оно называется плечом. Крутящий момент M, который привел к повороту системы на угол θ вокруг некоторой оси, совершает следующую работу:
A = M*θ.
Здесь M выражается в Н*м, а угол θ в радианах.
Задача по физике на механическую работу
Как было сказано в статье, работа всегда совершается той или иной силой. Рассмотрим следующую интересную задачу.
Тело находится на плоскости, которая наклонена к горизонту под углом 25o. Соскальзывая вниз, тело приобрело некоторую кинетическую энергию. Необходимо рассчитать эту энергию, а также работу силы тяжести. Масса тела равна 1 кг, пройденный им по плоскости путь равен 2 метра. Сопротивлением трения скольжения можно пренебречь.
Выше было показано, что работу совершает только та часть силы, которая направлена вдоль перемещения. Нетрудно показать, что в данном случае вдоль перемещения будет действовать следующая часть силы тяжести:
F = m*g*sin(α).
Здесь α - угол наклона плоскости. Тогда работа вычисляется так:
A = m*g*sin(α)*S = 1*9,81*0,4226*2 = 8,29 Дж.
То есть сила тяжести совершает положительную работу.
Теперь определим кинетическую энергию тела в конце спуска. Для этого вспомним второй ньютоновский закон и рассчитаем ускорение:
a = F/m = g*sin(α).
Поскольку соскальзывание тела является равноускоренным, то мы вправе воспользоваться соответствующей кинематической формулой для определения времени движения:
S = a*t2/2 =>
t = √(2*S/a) = √(2*S/(g*sin(α))).
Скорость тела в конце спуска рассчитывается так:
v = a*t = g*sin(α)*√(2*S/(g*sin(α))) = √(2*S*g*sin(α)).
Кинетическая энергия поступательного движения определяется с помощью следующего выражения:
E = m*v2/2 = m*2*S*g*sin(α)/2 = m*S*g*sin(α).
Мы получили интересный результат: оказывается, формула для кинетической энергии точно совпадает с выражением для работы силы тяжести, которое было получено ранее. Это свидетельствует о том, что вся механическая работа силы F направлена на увеличение кинетической энергии скользящего тела. В действительности из-за сил трения работа A всегда оказывается больше энергии E.


























