Обратная пропорция - это математическая зависимость, при которой с увеличением одной величины другая уменьшается, и наоборот. Это универсальный принцип, который проявляется в самых разных сферах нашей жизни.
Рассмотрим несколько примеров обратной пропорции.
В математике
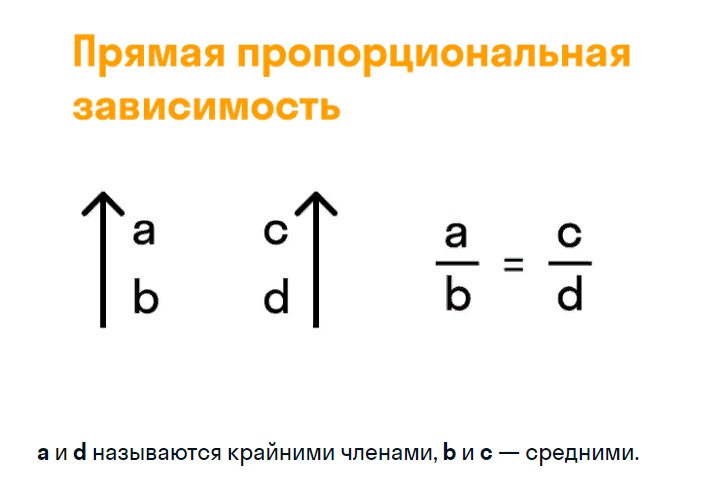
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
В физике
Один из самых известных примеров - зависимость между напряжением и сопротивлением в электрической цепи. Чем выше сопротивление, тем меньше сила тока при одинаковом напряжении. Это и есть обратная пропорция.
В химии
Еще один классический пример - зависимость скорости химической реакции от концентрации реагирующих веществ. Чем больше концентрация, тем быстрее идет реакция. Здесь тоже прослеживается обратная пропорция.
В экономике
В экономической теории есть закон спроса и предложения. Чем выше цена товара, тем меньше людей готовы его купить. А чем ниже цена, тем больше спрос. Это пример действия обратной пропорции на практике.

В медицине
В фармакологии существует понятие доза-эффект. Чем больше доза лекарства, тем сильнее его действие. Но после определенного предела эффективность не растет, а начинает снижаться из-за токсичности. Здесь мы видим прямую и обратную пропорцию в действии.
В повседневной жизни
Обратная пропорциональность проявляется и в наших обыденных делах. Например, чем больше людей садится в автобус, тем меньше свободного места там остается. И наоборот, чем меньше пассажиров, тем просторнее в салоне.
Еще один пример: чем выше человек поднимается по карьерной лестнице, тем меньше у него свободного времени. Потому что ответственность и нагрузка возрастают.
Таким образом, обратная пропорция - это универсальный закон, который проявляется в самых разнообразных сферах. Чтобы его понять, достаточно уловить взаимосвязь: одно растет - другое падает. И наоборот.
Как решать задачи на обратную пропорцию
Хотя обратная пропорциональность - довольно простая закономерность, решение соответствующих задач может вызывать затруднения. Давайте разберем пошаговый алгоритм.
- Определите, какие величины находятся в обратной зависимости.
- Запишите формулу обратной пропорциональности: a = k/b, где a и b - искомые величины, k - коэффициент пропорциональности.
- Найдите коэффициент пропорциональности, подставив известные значения a и b.
- Используя полученное уравнение, вычислите неизвестную величину.
Такой подход позволяет шаг за шагом решить задачу на обратную пропорцию. Главное - верно определить, какие величины связаны обратной зависимостью, остальное - математика.
Интересные факты
- Обратная пропорциональность называется также обратной зависимостью или обратной причинно-следственной связью.
- В древности об обратной пропорции писал еще Аристотель, определив это понятие как "отношение величин, одна из которых увеличивается тем более, чем меньше другая".
- Наиболее точные законы обратной пропорциональности были сформулированы Галилео Галилеем при изучении падения тел и маятника.
- Обратно пропорциональные величины часто обозначаются латинскими буквами x и y именно в таком порядке (x/y=k), по традиции, идущей от Галилея.
- Закон обратных квадратов - частный случай обратной пропорциональности, широко используемый в физике при описании гравитации и электромагнетизма.
Как видим, обратная пропорциональность или обратно пропорциональная зависимость - не просто абстрактное математическое понятие. Это фундаментальный закон природы, который помогает объяснить многие явления в окружающем нас мире.
Применение на практике
Понимание обратной пропорции важно не только для решения школьных задач. Этот принцип широко используется в различных областях:
- В экономике - для анализа спроса и предложения, определения оптимальной цены.
- В медицине - для расчета доз лекарственных препаратов.
- В технике - для подбора соотношения напряжения и силы тока.
- В экологии - для выявления взаимосвязей в природных системах.
- В психологии - для исследования мотивации и принятия решений.
Знание законов обратной пропорциональности помогает решать практические задачи в самых разных сферах деятельности. Это универсальный и мощный инструмент для моделирования реальных процессов и прогнозирования результатов.
Примеры обратной пропорции в искусстве и литературе
Обратная пропорциональность находит интересное отражение и в творчестве. Рассмотрим несколько примеров.
В живописи часто используется прием уменьшения размеров удаленных объектов. Чем дальше находится предмет, тем он меньше на картине. Это и есть проявление обратной перспективы.
В музыке при увеличении частоты звука его высота повышается. И наоборот, чем ниже частота, тем глубже звучание. Мы вновь наблюдаем обратную зависимость.
В литературе обратная пропорция часто используется как художественный прием. Например, чем выше взлетает герой, тем больнее его eventual падение. И наоборот, из глубокого упадка возможно возвышение.
Исторические аспекты обратной пропорции
Обратная пропорциональность известна человечеству с древности. Но понимание этого феномена менялось с течением истории.
В античности обратную зависимость связывали с гармонией мироздания. Считалось, что так природа поддерживает равновесие.
В Средние века к обратной пропорции относились настороженно, как к нарушению божественного порядка. Ее изучали в основном алхимики и астрологи.
В эпоху Возрождения великие ученые как Галилей стали использовать обратную пропорцию для формулировки физических законов. Это положило начало научному изучению.
Сегодня мы понимаем, что обратная зависимость - фундаментальный принцип организации нашего мира, действующий на всех уровнях.
Обратная пропорция в искусственном интеллекте
Обратная пропорциональность находит применение и в современных технологиях искусственного интеллекта. Рассмотрим несколько примеров.
В машинном обучении используется метод градиентного спуска, где на каждой итерации веса обновляются пропорционально градиенту ошибки. Чем ближе к оптимуму, тем меньше величина градиента.
В компьютерном зрении применяют обратную перспективу - чем дальше объект, тем меньше его размер на изображении. Это помогает определять расстояние.
В робототехнике используют принцип обратной связи - чем больше отклонение от заданной траектории, тем сильнее корректирующее управляющее воздействие. И наоборот.
Философский аспект обратной пропорции
Наконец, обратная пропорциональность имеет и философское измерение. Она учит нас видеть скрытые взаимосвязи явлений и понимать диалектику бытия.
Когда одно растет, а другое убывает - это закон природы. Но так устроена и человеческая жизнь. Успех в одной сфере часто означает потери в другой. Наша задача - научиться находить оптимальный баланс.
Обратная пропорция демонстрирует относительность любых ценностей. Великое может обернуться ничтожным, а из праха возникает новая жизнь. Все течет, все изменяется.
Постигая закон обратной зависимости, мы постигаем мудрость жизни, в которой всему свое время и место под солнцем. И это помогает нам жить в гармонии с миром и самими собой.



























