Расчет на устойчивость является обязательной и важной частью проектирования любых несущих конструкций - от мостов и высотных зданий до обычных металлических или деревянных балок. От правильности и точности этого расчета напрямую зависит безопасность людей, которые будут использовать эти конструкции. Давайте разберемся в тонкостях расчета на устойчивость стержня.
Сущность расчета на устойчивость стержня
Расчет на устойчивость стержня заключается в определении так называемой критической силы или критического напряжения, при котором прямолинейный сжатый стержень теряет устойчивость и начинает изгибаться. Это происходит из-за того, что стержень под действием сжимающей силы выходит из первоначального положения равновесия.
Устойчивость стержня зависит от его геометрических размеров, условий закрепления концов, жесткости материала и ряда других факторов.
Критерием оценки устойчивости служит соотношение между критической силой или критическим напряжением и фактически действующей силой или напряжением в стержне. Фактические напряжения не должны превышать критические, иначе возникает опасность потери устойчивости.
Потеря устойчивости часто приводит к поломке и обрушению конструкций. Поэтому расчет на устойчивость крайне важен для обеспечения их надежности и долговечности.
Основные методы расчета на устойчивость
Для определения критической силы или критического напряжения стержня используются разные подходы в зависимости от его гибкости и условий работы:
- Формула Эйлера - для стержней большой гибкости в упругой стадии работы материала;
- Эмпирические формулы (Ясинского и др.) - для стержней средней гибкости с упругопластическими деформациями;
- Метод коэффициента запаса - для стержней любой гибкости путем введения поправочных коэффициентов;
- Графики и номограммы - для упрощения расчетов с использованием готовых зависимостей.
Рассмотрим подробнее формулу Эйлера, как наиболее распространенный метод расчета на устойчивость стержня:
Формула Эйлера для определения критического напряжения:
σкр = (π2*E*Imin) / (A*(μ*l)2)
где E - модуль упругости материала; Imin - наименьший момент инерции сечения; A - площадь поперечного сечения; μ - коэффициент приведенной длины; l - расчетная длина стержня.
Как видно из формулы, на величину критического напряжения влияют: жесткость материала, геометрические размеры сечения, расчетная длина и условия закрепления стержня.
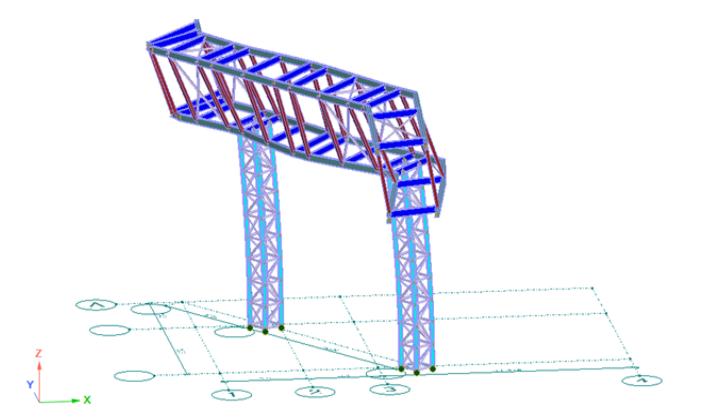
Учет условий закрепления стержня
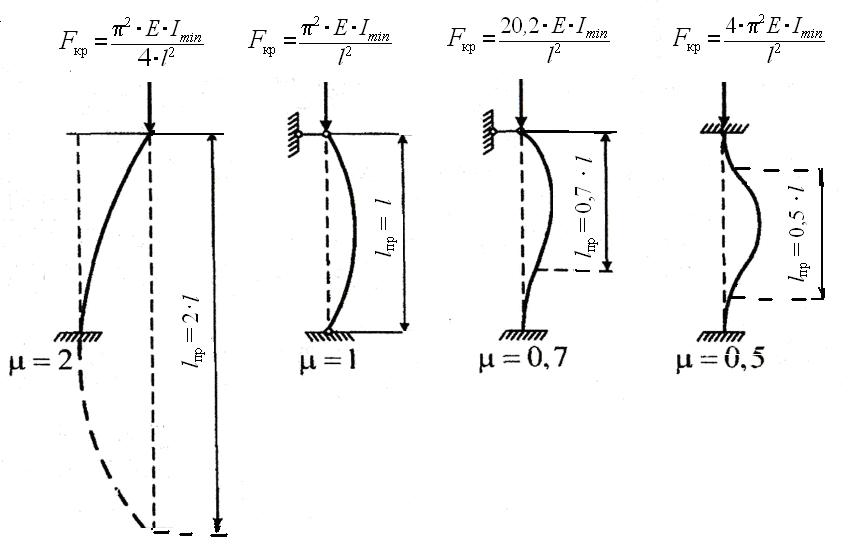
Условия закрепления концов существенно влияют на устойчивость стержня. Рассмотрим основные схемы закрепления:
- Шарнирно-неподвижное;
- Жестко-неподвижное;
- Жестко-шарнирное;
- Жестко-жесткое;
Для учета закреплений в формулу Эйлера вводится коэффициент приведенной длины μ. Он показывает, во сколько раз уменьшается критическая сила по сравнению с идеальным шарнирно-неподвижным закреплением.
| Тип закрепления концов | Коэффициент μ |
| Шарнирно-неподвижное | 1 |
Как видно из таблицы, наиболее неблагоприятный случай - шарнирно-неподвижное закрепление (μ=1), так как здесь критическая сила имеет наименьшее значение.
Помимо μ, для учета длины стержня используется понятие приведенной длины lпр = μ*l. Она может существенно отличаться от фактической длины стержня.
Выполнение проверочных расчетов
Проверочный расчет на устойчивость стержня выполняют по следующему алгоритму:
- Определяют геометрические характеристики поперечного сечения стержня;
- Вычисляют коэффициент приведенной длины μ исходя из закрепления концов;
- Находят критическое напряжение по формуле Эйлера;
- Сравнивают критическое и фактическое напряжения в стержне.
Рассмотрим численный пример расчета на устойчивость для стержня прямоугольного сечения с размерами: h=5 см, b=10 см, l=3 м. Материал стали, E=2*105 МПа. Концы шарнирно закреплены.
1. Вычисляем момент инерции сечения:
Imin = (bh3)/12 = (10*53)/12 = 104 см4
2. Коэффициент μ=1, так как закрепление шарнирно-неподвижное 3. Подставляем значения в формулу Эйлера: σкр = (3,142*2*105*104) / (10*5*(1*3)2) = 421 МПа
Как видно из примера, расчет на устойчивость не является очень сложным. Главное - правильно определить исходные данные и выбрать подходящую расчетную формулу. При соблюдении этих условий можно получить надежные результаты.
Проектирование сечения стержня
Проектировочный расчет на устойчивость стержня проводят с целью подбора размеров поперечного сечения исходя из заданных нагрузок и условий работы.
Последовательность проектировочного расчета:
- Задаются исходными данными - материал, длина, условия закрепления, внешняя нагрузка;
- По этим данным определяется необходимый минимальный момент инерции сечения;
- Подбираются размеры сечения, удовлетворяющие расчетному моменту инерции;
- Проверяется выполнение условия устойчивости для подобранного сечения.
После подбора сечения по расчету, подбирают подходящий стандартный профиль из сортамента с близкими характеристиками.
Расчет устойчивости гибких стержней
К гибким стержням относят стержни, у которых гибкость λ > 100. У таких стержней возможны значительные деформации изгиба, поэтому вместо жесткости EI используется жесткость при изгибе EIz.
Для расчета устойчивости гибкого стержня используется дифференциальное уравнение изогнутой оси в виде:
EIz*d4y/dx4 + q(x) = 0
где q(x) - поперечная нагрузка, зависящая от координаты x.
Решение этого уравнения позволяет найти критическую нагрузку для гибкого стержня с заданными граничными условиями.
Особенности расчета деревянных стержней
Для деревянных стержней характерна анизотропия механических свойств в разных направлениях. Это необходимо учитывать при расчете на устойчивость. Кроме того, используются особые эмпирические зависимости.
Учет анизотропии древесины
При расчете на устойчивость деревянных стержней необходимо учитывать анизотропию древесины - различие механических характеристик (модули упругости, пределы прочности) в разных направлениях.
Выделяют три главных направления анизотропии:
- Продольное - вдоль волокон;
- Радиальное - перпендикулярно к волокнам, в радиальном направлении;
- Тангенциальное - перпендикулярно к волокнам, в tangential направлении.
При расчете на устойчивость учитывают наименьшую жесткость древесины, как правило, в радиальном или тангенциальном направлении.
Центрально сжатые деревянные стержни
Если сжимающая сила центрально приложена вдоль оси стержня, волокна древесины ориентированы в этом же направлении, то можно использовать бóльшие значения модуля упругости и пределов прочности на сжатие для древесины.
Это позволяет увеличить несущую способность центрально сжатых деревянных стоек и балок по сравнению с изгибаемыми элементами при тех же габаритных размерах сечения.
Коэффициенты запаса для дерева
В расчетах на устойчивость деревянных конструкций рекомендуется применять повышенные коэффициенты запаса:
- Для устойчивости ny = 2,5÷3,5;
- Для прочности n = 5÷6.
Это связано с анизотропией и неоднородностью древесины, а также возможным влиянием влажности и температуры.
Продольная устойчивость деревянных элементов
Особого внимания требует обеспечение продольной устойчивости сжатых и изгибаемых деревянных элементов, у которых возможно развитие продольных трещин вдоль волокон древесины.
Для предотвращения развития таких трещин ограничивают относительную деформацию сжатой зоны сечения на уровне 2,5-3,5%.