Биссектриса угла параллелограмма - важное понятие школьного курса геометрии. Знание ее свойств позволяет решать множество практических задач. В статье рассматриваются такие вопросы, как определение биссектрисы угла, ее основные свойства в параллелограмме, применение для решения задач на вычисление углов, сторон, периметра.
Определение биссектрисы угла параллелограмма
Биссектриса угла параллелограмма - это отрезок, соединяющий вершину угла с точкой на противоположной стороне таким образом, что делит угол пополам. Биссектриса может быть проведена из каждой вершины параллелограмма.
Биссектриса угла параллелограмма обладает несколькими важными свойствами, позволяющими эффективно использовать ее при решении задач.
Основное свойство биссектрисы угла параллелограмма заключается в том, что она делит противоположную сторону на два равных отрезка. Это вытекает из определения биссектрисы и свойств параллелограмма (равенства противоположных сторон). Благодаря этому свойству по известной биссектрисе можно найти длины отрезков противоположной стороны.
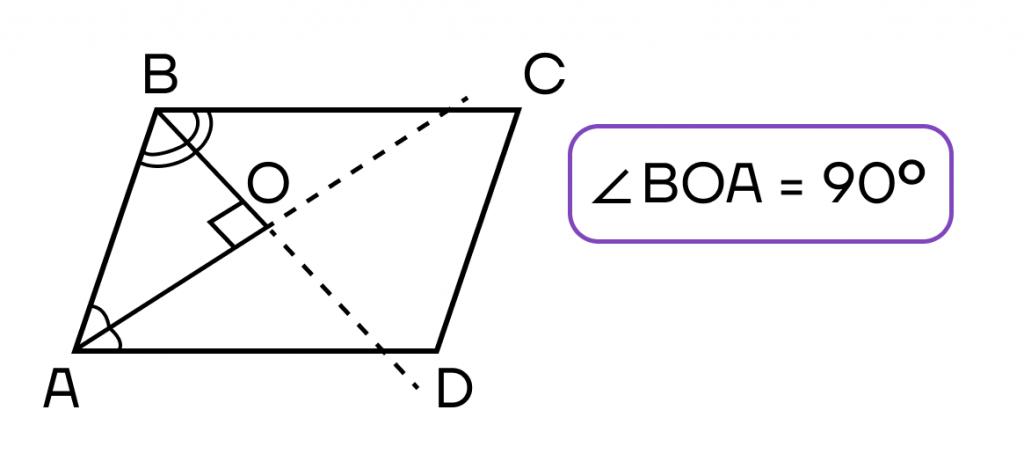
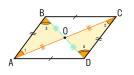
Еще одно важное свойство биссектрисы - перпендикулярность биссектрис смежных углов параллелограмма. Это следует из того, что сумма смежных углов параллелограмма равна 180 градусов, а биссектриса делит угол пополам. Таким образом, биссектрисы смежных углов образуют прямой угол.
Биссектрисы противоположных углов параллелограмма параллельны. Это также вытекает из особенностей параллелограмма: противоположные углы равны, значит их биссектрисы параллельны.
Еще одно следствие: точка пересечения биссектрис двух смежных углов принадлежит противоположной стороне параллелограмма. Это позволяет находить координаты вершин параллелограмма относительно известных точек.
Таким образом, свойства биссектрисы углов параллелограмма позволяют находить длины сторон, координаты вершин и величины углов. Правильное использование этих свойств - ключ к решению многих задач на вычисление элементов параллелограмма.
Применение биссектрисы для решения задач на вычисление элементов параллелограмма
Биссектриса угла параллелограмма является очень полезным инструментом при решении задач на вычисление различных элементов параллелограмма.
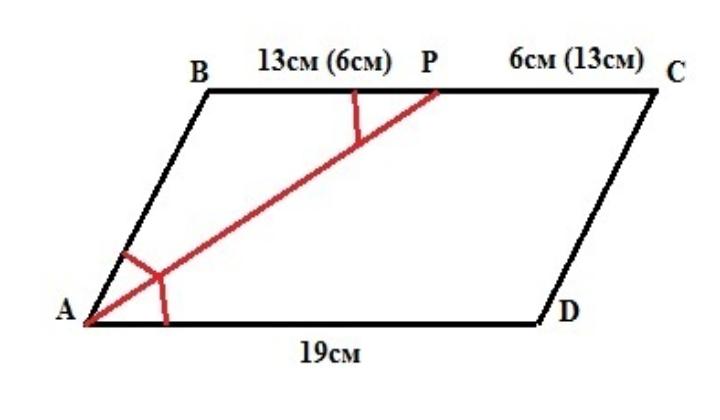
Одна из самых распространенных задач - найти длину стороны параллелограмма, если известна величина угла и положение биссектрисы этого угла. Используя свойство биссектрисы делить противоположную сторону пополам, по длине биссектрисы можно найти длину искомой стороны.
Если в задаче требуется найти величину угла параллелограмма, а известно положение его биссектрисы, можно воспользоваться свойством перпендикулярности биссектрис смежных углов. Построив перпендикуляр к известной биссектрисе, получим биссектрису смежного угла, что позволит найти искомый угол.
Часто в задачах на параллелограмм требуется найти координаты его вершин. Если известна точка пересечения биссектрис двух смежных углов, то по свойству принадлежности этой точки противоположной стороне можно найти координаты двух вершин.
Также с помощью биссектрисы можно находить периметры, площади, отдельные отрезки сторон параллелограмма. Для этого используются свойства равенства отрезков противоположной стороны, образования равнобедренного треугольника и другие.
Особенно эффективно сочетание свойств биссектрисы с другими свойствами параллелограмма - равенством противоположных сторон, параллельностью сторон и др. Это позволяет получать разнообразные зависимости между элементами параллелограмма.
Таким образом, умелое использование биссектрисы в сочетании со свойствами параллелограмма - мощный инструмент решения широкого круга задач на вычисление различных элементов параллелограмма.