Квадрат является одной из самых простых, но в то же время удивительных геометрических фигур. У него есть множество интересных свойств, связанных с его диагоналями, которые не всегда очевидны, но очень полезны на практике.
В этой статье мы познакомимся с некоторыми неожиданными фактами о диагоналях квадрата, рассмотрим их доказательства и применение этих свойств для решения задач.
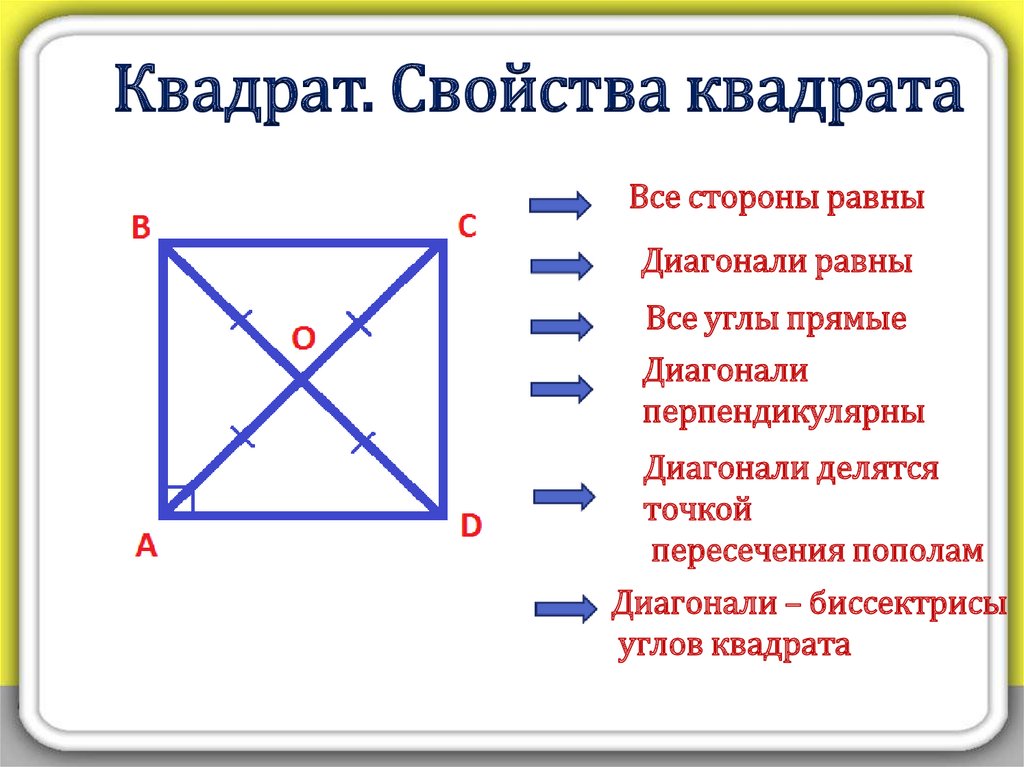
Диагонали квадрата равны
Одним из основных свойств диагоналей квадрата является их равенство. Это означает, что независимо от размера сторон квадрата, его диагонали всегда будут одинаковой длины.
Доказательство этого утверждения простое. Рассмотрим квадрат ABCD со стороной a. Поскольку это квадрат, то его противоположные стороны попарно равны: AB = DC и AD = BC. Кроме того, углы квадрата - прямые. Следовательно, треугольники ABC и CDA - равнобедренные с равными боковыми сторонами AB = DC и равными углами при вершинах B и D. По признаку равенства треугольников эти треугольники равны, в том числе равны их гипотенузы - диагонали AC и BD.
Таким образом, в любом квадрате его диагонали равны. Это важное свойство часто используется при решении геометрических задач, связанных с квадратом.
Диагонали квадрата пересекаются под прямым углом
Еще одним важным свойством диагоналей квадрата является то, что они пересекаются под прямым углом (90 градусов). Это происходит благодаря тому, что квадрат обладает свойством прямоугольности, то есть все его углы равны 90 градусам.
Чтобы доказать, что угол между диагоналями квадрата прямой, достаточно рассмотреть любые два треугольника с общей стороной - диагональю AC. Например, треугольники ABC и ADC. Угол ABC - прямой, так как принадлежит квадрату ABCD. Аналогично, угол ADC - тоже прямой. Значит, третий угол ACD, лежащий напротив стороны AC, должен быть прямым согласно свойству треугольника (сумма всех углов треугольника равна 180 градусам).
Таким образом, диагонали любого квадрата всегда пересекаются под прямым углом. Это свойство используется, когда нужно доказать, что четырехугольник является квадратом - достаточно показать, что его диагонали взаимно перпендикулярны.
Точка пересечения диагоналей квадрата делит их пополам
Точка пересечения двух диагоналей квадрата является их общей точкой. Обозначим ее буквой O. Эта точка обладает интересным свойством - она делит каждую диагональ пополам, то есть на два равных отрезка.
Это можно доказать, используя ранее рассмотренное свойство диагоналей - их равенство. Рассмотрим диагональ AC. Треугольник AOB равнобедренный, так как его боковые стороны АО и OB являются радиусами одной и той же окружности (описанной около квадрата). Значит, отрезки AO = OB. «свойства диагоналей квадрата» Аналогично для второй диагонали BD справедливо равенство отрезков BO = OD.
Итак, точка пересечения O делит диагонали квадрата пополам. Это свойство часто применяется в задачах на доказательство того, что данный четырехугольник является квадратом.
Применение свойств диагоналей квадрата для решения задач
Рассмотренные выше свойства диагоналей квадрата часто используются при решении геометрических задач, связанных с этой фигурой. Давайте рассмотрим несколько примеров таких задач, чтобы понять, как применять знание свойств диагоналей на практике.
Задача 1. Дан четырехугольник ABCD. Докажите, что это квадрат. Решение. По условию известно только то, что ABCD - четырехугольник. Необходимо доказать, что он является квадратом. Для этого воспользуемся свойствами его диагоналей:
- Проведем диагонали AC и BD. Измерим их - они равны.
- Угол между диагоналями измерим - он равен 90 градусов.
- Найдем точку пересечения O диагоналей. Измерим отрезки AO, OB, CO и DO - они равны.
Так как диагонали четырехугольника удовлетворяют всем рассмотренным выше свойствам диагоналей квадрата, то данный четырехугольник ABCD является квадратом.






















