Сокращению обыкновенной дроби учат еще в школе на уроках математики. Если вы школьник, который благополучно пропустил эту тему мимо ушей или не понял ее, или если вы родитель такого школьника, то эта тема как раз для вас. Как сократить дробь? Легко и просто, если вы последуете методу, представленному ниже.
Что такое обыкновенная дробь
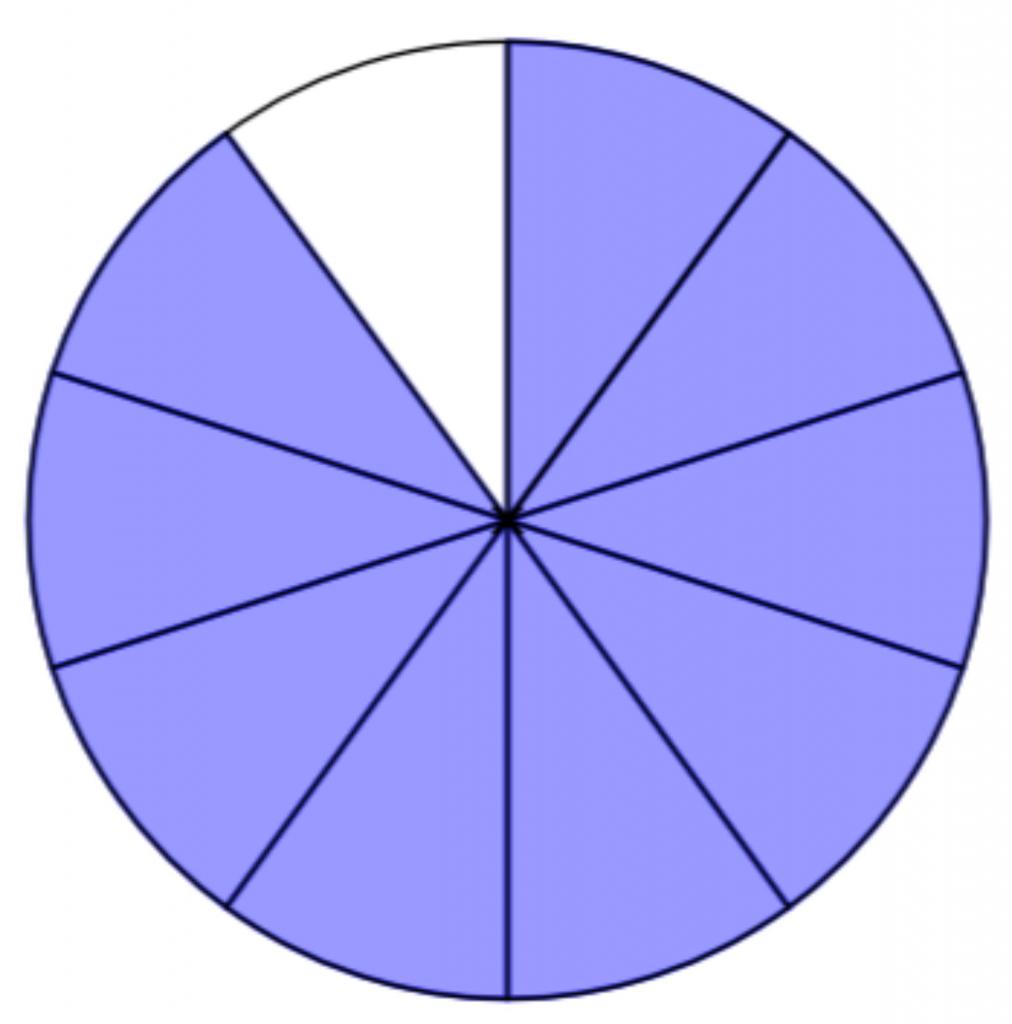
Вспомним теорию. Обыкновенные дроби появляются вследствие деления какого-либо предмета или единицы измерения на несколько равных частей. В пример возьмем пирог. Если его разрезать на десять частей и дать эти десять частей десятерым гостям, то в обыкновенной дроби это будет выглядеть как 1/10 (одна десятая часть). Но на письме это будет отражено двухэтажной записью, в которой над черточкой число, обозначающее то, сколько частей взяли, а под черточкой общее их количество.
Например, дробь 2/5 означает, что человек из пяти частей чего-либо взял только две.
Переходим к главному вопросу: как сократить дробь?
Что это значит
Сократить дробь - значит разделить числитель (число над чертой) и знаменатель (под чертой) на одно и то же число (оно должно быть больше единицы). Причем разделять нужно до того момента, пока для числителя и знаменателя не останется общего числа, на которое их можно было бы разделить.
Сокращенные дроби - это дроби, которые дальше сокращаться уже не могут. Они не считаются сокращенными, если числитель и знаменатель все еще имеют общее число, на которое можно разделить каждый из них.
Сокращение
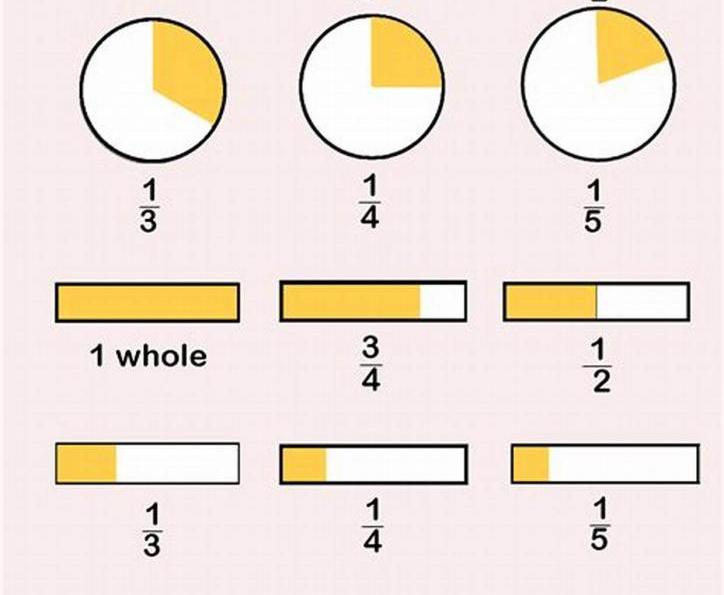
С этим разобрались, переходим к следующему вопросу. Рассмотрим на примерах, как сократить дробь.
Возьмем дробь 5/25. На какое число делим? На пять. Сократим числитель и знаменатель на него. В итоге получится число 1/5. Можно ли сокращать дальше? Нет.
Или дробь 60/120. На какое число их можно разделить? На тридцать. Сократим и получим число 2/4. Можно ли сокращать дальше? Да, можно сократить еще на два. Получится 1/2.
Как сократить дробь "до победного числа", то есть не делить ее несколько раз? Просто старайтесь найти наибольшее число, на которое делятся числитель и знаменатель. Когда мы разбирали второй пример, дробь 60/120, ее можно было бы разделить на шестьдесят и сразу получить 1/2.
Если же наибольшее число сразу не находится, то попробуйте сначала разделить дробь на любое число, которое пришло вам в голову, и попробуйте поработать уже с новой дробью снова. Главное - правильно и до конца сократить дробь. Совершенно не важно, сколько шагов вы для этого сделали, но если вы дорожите своим временем, постарайтесь выполнить все за один шаг.





















