Что такое равенство? Первый признак и принципы равенства

«Равенство» - это тема, которую ученики проходят еще в начальной школе. Сопутствует ей также ей «Неравенства». Эти два понятия тесно взаимосвязаны. Кроме того, с ними связывают такие термины, как уравнения, тождества. Итак, что такое равенство?

Понятие равенства

Под этим термином понимают высказывания, в записи которых есть знак «=». Равенства разделяются на верные и неверные. Если в записи вместо = стоит <, >, тогда речь идет о неравенствах. Кстати, первый признак равенства говорит о том, что обе части выражения идентичны по своему результату или записи.

Кроме понятия равенства, в школе изучают также тему «Числовое равенство». Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака =. К примеру, 2*5+7=17. Обе части записи равны между собой.

В числовых выражениях подобного типа могут использоваться скобки, влияющие на порядок действий. Итак, существует 4 правила, которые следует учесть при вычислении результатов числовых выражений.

1. Если в записи нет скобок, тогда действия выполняются с высшей ступени: III→II→I. Если есть несколько действий одной категории, тогда они выполняются слева направо.
2. Если в записи есть скобки, тогда действие выполняется в скобках, а затем с учетом ступеней. Возможно, в скобках будет несколько действий.
3. Если выражение представлено в виде дроби, тогда вычислять нужно сначала числитель, потом знаменатель, затем числитель делится на знаменатель.
4. Если в записи есть вложенные скобки, тогда вычисляется сначала выражение во внутренних скобках.

Итак, теперь понятно, что такое равенство. В дальнейшем будут рассмотрены понятия уравнения, тождества и способы их вычисления.

Свойства числовых равенств

Что такое равенство? Изучение этого понятия требует знания свойств числовых тождеств. Приведенные ниже текстовые формулы позволяют лучше изучить данную тему. Конечно, эти свойства больше подходят для изучения математики в старших классах.

1. Числовое равенство не будет нарушено, если в обеих его частях прибавить одно и то же число к существующему выражению.

А = В ↔ А + 5 = В + 5

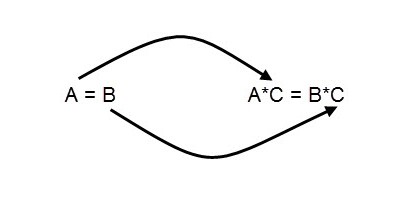
2. Не будет нарушено уравнение, если обе его части умножить или разделить на одно и то же число или выражение, которые отличны от нуля.

Р = О ↔ Р ∙ 5 = О ∙ 5

Р = О ↔ Р : 5 = О : 5

3. Прибавив к обеим частям тождества одинаковую функцию, которая имеет смысл при любых допустимых значениях переменной, мы получим новое равенство, равносильное первоначальному.

F(X) = Ψ(X) ↔ F(X) + R(X) = Ψ(X) + R(X)

4. Любое слагаемое или выражение можно перенести по другую сторону знака равенства, при этом нужно поменять знаки на противоположные.

Х + 5 = У – 20 ↔ Х = У – 20 – 5 ↔ Х = У – 25

5. Умножив или разделив обе части уравнения на одну и ту же функцию, отличную от нуля и имеющую смысл для каждого значения Х из ОДЗ, мы получим новое уравнение, равносильное первоначальному.

F(X) = Ψ(X) ↔ F(X) ∙ R(X) = Ψ(X) ∙ R(X)

F(X) = Ψ(X) ↔ F(X) : G(X) = Ψ(X) : G(X)

Приведенные правила в явной степени указывают на принцип равенства, который существует при определенных условиях.

Понятие пропорции

В математике существует такое понятие, как равенство отношений. В этом случае подразумевается определение пропорции. Если разделить А на В, то результатом будет отношение числа А к числу В. Пропорцией называют равенство двух отношений:

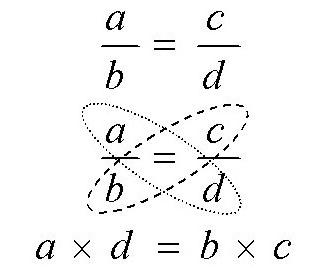
Иногда пропорция записывается следующим образом: A : B = C : D. Отсюда вытекает основное свойство пропорции: A * D = D * C, где A и D – крайние члены пропорции, а В и С – средние.

Тождества

Тождеством называют равенство, которое будет верно при всех допустимых значениях тех переменных, которые входят в задание. Тождества могут быть представлены как буквенные или числовые равенства.

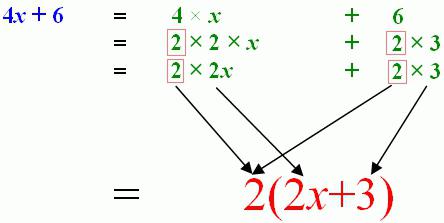
Тождественно равными называются выражения, содержащие в обеих частях равенства неизвестную переменную, которая способна приравнять две части одного целого.

Если проводить замены одного выражения другим, которое будет равно ему, тогда речь идет о тождественном преобразовании. В этом случае можно воспользоваться формулами сокращенного умножения, законами арифметики и прочими тождествами.

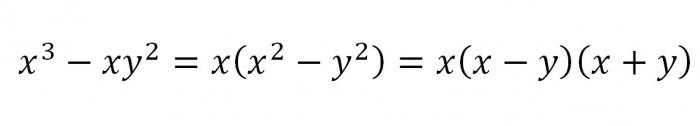
Чтобы сократить дробь, нужно провести тождественные преобразования. К примеру, дана дробь. Чтобы получить результат, следует воспользоваться формулами сокращенного умножения, разложением на множители, упрощением выражений и сокращением дробей.

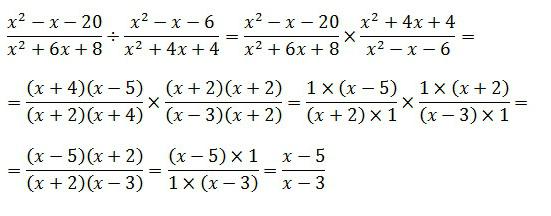
При этом стоит учесть, что данное выражение будет тождественным тогда, когда знаменатель не будет равен 3.

5 способов доказать тождество

Чтобы доказать равенство тождественное, нужно провести преобразование выражений.

I способ

Необходимо провести равносильные преобразования в левой части. В результате получается правая часть, и можно говорить о том, что тождество доказано.

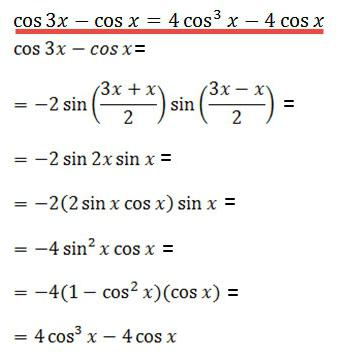
II способ

Все действия по преобразованию выражения происходят в правой части. Итогом проделанных манипуляций является левая часть. Если обе части идентичны, то тождество доказано.

III способ

«Трансформации» происходят в обеих частях выражения. Если в результате получатся две идентичные части, тождество доказано.

IV способ

Из левой части вычитается правая. В результате равносильных преобразований должен получиться нуль. Тогда можно говорить о тождественности выражения.

V способ

Из правой части вычитается левая. Все равносильные преобразования сводятся к тому, чтобы в ответе стоял нуль. Только в таком случае можно говорить о тождественности равенства.

Основные свойства тождеств

В математике зачастую используют свойства равенств, чтобы ускорить процесс вычисления. Благодаря основным алгебраическим тождествам процесс вычисления некоторых выражений займет считанные минуты вместо долгих часов.

• Х + У = У + Х
• Х + (У + С) = (Х + У) + С
• Х + 0 = Х
• Х + (-Х) = 0
• Х ∙ (У + С) = Х∙У + Х∙С
• Х ∙ (У – С) = Х∙У – Х∙С
• (Х + У) ∙ (С + Е) = Х∙С + Х∙Е + У∙С + У∙Е
• Х + (У + С) = Х + У + С
• Х + (У – С) = Х + У – С
• Х – (У + С) = Х – У – С
• Х – (У – С) = Х – У + С
• Х ∙ У = У ∙ Х
• Х ∙ (У ∙ С) = (Х ∙ У) ∙ С
• Х ∙ 1 = Х
• Х ∙ 1/Х = 1, где Х ≠ 0

Формулы сокращенного умножения

По своей сути формулы сокращенного умножения являются равенствами. Они помогают решить множество задач в математике благодаря своей простоте и легкости в обращении.

• (А + В)² = А² + 2∙А∙В + В² – квадрат суммы пары чисел;

• (А – В)² = А² – 2∙А∙В + В² – квадрат разности пары чисел;

• (С + В) ∙ (С – В) = С² – В² – разность квадратов;

• (А + В)³ = А³ + 3∙А²∙В + 3∙А∙В² + В³ – куб суммы;

• (А – В)³ = А³ – 3∙А²∙В + 3∙А∙В² – В³ – куб разности;

• (Р + В) ∙ (Р² – Р∙В + В²) = Р³ + В³ – сумма кубов;

• (Р – В) ∙ (Р² + Р∙В + В²) = Р³ – В³ – разность кубов.

Формулы сокращенного умножения зачастую применяются, если необходимо привести многочлен к привычному виду, упростив его всеми возможными способами. Представленные формулы доказываются просто: достаточно раскрыть скобки и привести подобные слагаемые.

Уравнения

После изучения вопроса, что такое равенство, можно приступать к следующему пункту: что такое уравнение. Под уравнением понимается равенство, в котором присутствуют неизвестные величины. Решением уравнения называют нахождение всех значений переменной, при которых обе части всего выражения будут равны. Также встречаются задания, в которых нахождение решений уравнения невозможно. В таком случае говорят, что корней нет.

Как правило, равенства с неизвестными в качестве решения выдают целые числа. Однако возможны случаи, когда корнем являются вектор, функция и другие объекты.

Уравнение является одним из важнейших понятий в математике. Большинство научных и практических задач не позволяют измерить или вычислить какую-либо величину. Поэтому необходимо составлять соотношение, которое удовлетворит все условия поставленной задачи. В процессе составления такого соотношения появляется уравнение или система уравнений.

Обычно решение равенства с неизвестным сводится к преобразованию сложного уравнения и сведению его к простым формам. Необходимо помнить, что преобразования нужно проводить относительно обеих частей, в противном случае на выходе получится неверный результат.

4 способа решить уравнение

Под решением уравнения понимают замену заданного равенства другим, которое равносильно первому. Подобная подмена известна как тождественное преобразование. Чтобы решить уравнение, необходимо воспользоваться одним из способов.

1. Одно выражение заменяется другим, которое в обязательном порядке будет тождественно первому. Пример: (3∙х+3)²=15∙х+10. Это выражение можно преобразовать в 9∙х²+18∙х+9=15∙х+10.

2. Перенесение членов равенства с неизвестным из одной стороны в другую. В таком случае необходимо правильно менять знаки. Малейшая ошибка сгубит всю проделанную работу. В качестве примера возьмем предыдущий «образец».

9∙х² + 12∙х + 4 = 15∙х + 10

9∙х² + 12∙х + 4 – 15∙х – 10 = 0

9∙х² – 3∙х – 6 = 0

Дальше уравнение решается с помощью дискриминанта.

3. Перемножение обеих частей равенства на равное число или выражение, которые не равняются 0. Однако стоит напомнить, что если новое уравнение не будет равносильным равенству до преобразований, тогда количество корней может существенно измениться.

4. Возведение в квадрат обеих частей уравнения. Этот способ просто замечательный, особенно когда в равенстве есть иррациональные выражения, то есть квадратный корень и выражение под ним. Тут есть один нюанс: если возвести уравнение в четную степень, тогда могут появиться посторонние корни, которые исказят суть задания. И если неправильно извлечь корень, тогда смысл вопроса в задаче будет неясен. Пример: │7∙х│=35 → 1) 7∙х = 35 и 2) – 7∙х = 35 → уравнение будет решено верно.

Итак, в этой статье упоминаются такие термины, как то уравнения и тождества. Все они происходят от понятия «равенство». Благодаря различного рода равносильным выражениям решение некоторых задач в значительной мере облегчено.