Процесс распространения света в однородном прозрачном веществе и законы его взаимодействия с разными препятствиями (непрозрачными объектами, границами раздела прозрачных сред, отверстиями) на протяжении всей истории интересовали ученых и философов. Разумное объяснение и математическое описание многих явлений, в которых свет ведет себя как волна, удалось получить благодаря использованию принципа Гюйгенса-Френеля. Что он означает и к каким выводам приводит, эти и другие вопросы раскрываются в статье.
Волновая теория света Гюйгенса и его принцип

Первые теории о природе света и законах его распространения в средах начали появляться в XVII веке. Одной из них была волновая теория Христиана Гюйгенса, голландского ученого, вклад которого в развитие современных представлений о свете является значительным.
Гюйгенс полагал, что свет - это волна, подобная звуку. Как и звук, для своего существования она нуждается в среде. Этой средой ученый считал эфир. Используя аналогию со звуком, Гюйгенс смог понять, как происходит движение световой волны в эфире. Это движение полностью описывается так называемым принципом Гюйгенса.
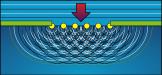
Предположим, что имеется некоторый источник плоских волн. Это означает, что волновая поверхность (поверхность одной фазы) представляет собой плоскость. Достигнув произвольной части пространства, каждая точка волнового фронта возбуждает локальную область эфира так, что та становится источником новой волны. Совокупность поверхностей новых или вторичных волн определяет результирующую поверхность фронта во время его движения.
Идея возбуждения каждой точкой фронта вторичных волн называется принципом Гюйгенса (см. рисунок выше).
Принцип Гюйгенса и фронт сферической и плоской волн
Покажем, используя принцип Гюйгенса, как можно строить волновые поверхности для фронта произвольной формы. Для простоты рассмотрим два типа фронта: плоский и сферический (см. рисунок ниже).
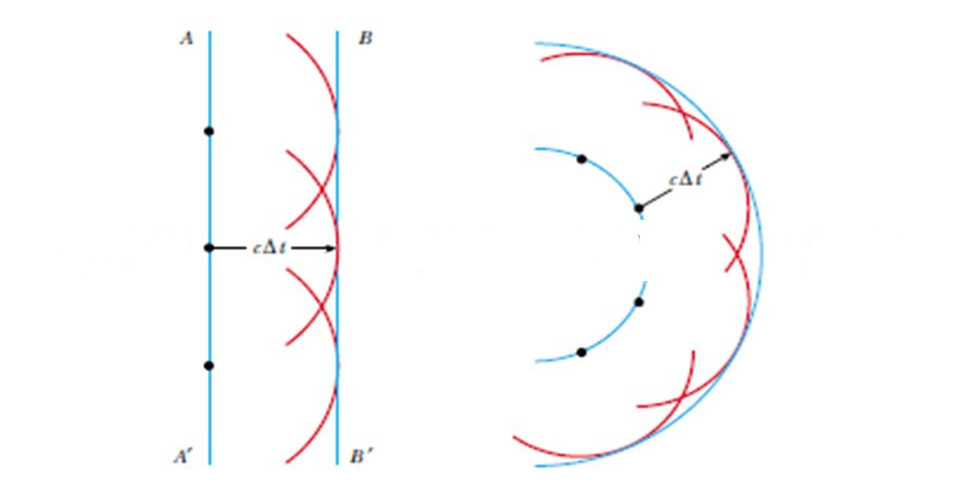
Предположим, что свет движется в однородной среде по всем направлениям одинаково со скоростью c. На левом рисунке представлен фронт AA' в некоторый нулевой момент времени. Определим его форму в момент времени Δt. Поскольку каждая точка фронта генерирует вторичные волны, то за время Δt они пройдут расстояние c * Δt. Если провести окружности этого радиуса от каждого из таких источников (три точки на фронте AA'), то касательная к окружностям определит фронт в момент времени Δt (BB').
Теперь рассмотрим сферический фронт на правом рисунке. Поступаем точно так же, как и в предыдущем случае: выбираем ряд точек на сферическом фронте, проводим окружности одинакового радиуса с центром в каждой из них, рисуем касательную ко всем окружностям (вторичным волнам). Как видим, в этом случае получается также сферический фронт, но уже большего радиуса.
Таким образом, принцип Гюйгенса объясняет, как распространяются световые волны в средах. Важно понимать, что при этом Гюйгенс не пользовался понятиями амплитуды или длины волны. Его принцип является исключительно геометрической идеей, основанной на аналогии с движением звука.
Принцип Гюйгенса-Френеля
Многие путают его с принципом Гюйгенса. Рассмотрим, в чем заключается принцип Гюйгенса-Френеля.
После того как мировое сообщество ученых приняло корпускулярную теорию Ньютона, о теории волн Гюйгенса забыли. Новое ее возрождение связано с именем француза Огюстена Френеля.

В 1801 году Томас Юнг провел свои знаменитые опыты с двумя щелями и получил дифракционную картину от монохроматического источника света. При этом картина получалась благодаря двум явлениям: дифракции и интерференции. Френель несколькими годами позже использовал экспериментальные данные Юнга и волновую теорию Гюйгенса для того, чтобы объяснить явления интерференции и дифракции.
Формулировка принципа Гюйгенса-Френеля, по сути, не отличается от таковой для принципа Гюйгенса, однако последний является числом геометрическим, Френель же внес в него физический смысл. Каждая точка фронта является источником вторичных волн, амплитуда которых падает обратно пропорционально расстоянию от источника. Чтобы определить результирующее колебание в данной точке, необходимо рассмотреть интерференцию всех вторичных волн движущегося фронта.
Формула результирующего колебания в произвольной точке
Из принципа Гюйгенса-Френеля формула для амплитуды колебаний в любой точке, которая находится впереди волнового фронта, получается достаточно легко.
Представим себе некоторый волновой фронт произвольной формы. Каждый его элемент площадью dS генерирует вторичную волну. В произвольной точке P, расположенной перед фронтом, элементарная волна приходит со следующей амплитудой:
dA = K * a0 * dS/r * cos(ω * t-k * r+α0).
Здесь r - расстояние от элемента dS до точки P, k - волновой вектор, ω - частота колебаний, α0 - начальная фаза, a0 - это амплитуда вторичной волны элемента dS, коэффициент K зависит от угла между направлением на точку P и перпендикуляром к площадке dS.
Если взять интегральную сумму по всем элементарным волнам фронта площадью S, тогда получится искомое колебание в точке P, то есть:
A = ∫SK(Φ) * a0 / r * cos(ω * t-k * r+α0)*dS.
Коэффициент K(Φ) примет максимальное значение для Φ = 0 и будет равен нулю для Φ = 90o.
Таким образом, при рассмотрении произвольного фронта волны принцип Гюйгенса-Френеля позволяет получить результирующее колебание в любой точке.
Понятие о зонах Френеля
Приведенная в предыдущем пункте формула является достаточно сложной с точки зрения математики. Даже для фронта сферической формы расчет приведенного интеграла - это громоздкая задача. Однако Френель показал, что ее можно заменить простой суммой, если фронт волны разбить на отдельные зоны в форме окружности. Причем толщина каждой зоны будет такой, чтобы расстояние от ее края до рассматриваемой точки (приемника) отличалась от аналогичного расстояние для предыдущей зоны на половину длины волны.
Если сферический фронт движется вдоль определенного направления, то от источника до приемника его форма будет похожа на растянутый в одном направлении шар. На рисунке ниже приведены зоны Френеля и волновой фронт между источником T и приемником R.
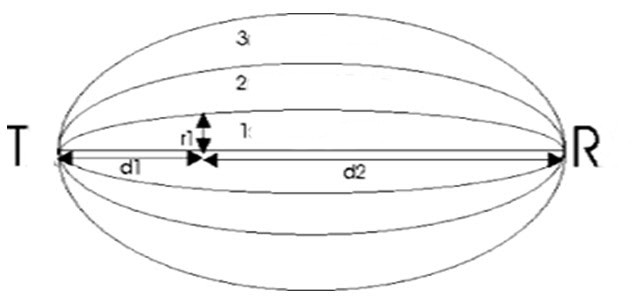
Использование зон Френеля для расчета амплитуды волны
Пользоваться зонами Френеля очень удобно. Поскольку каждая из них согласно принципу Гюйгенса-Френеля испускает вторичные волны, то от двух соседних зон к приемнику они приходят в противофазе. То есть соседние зоны ослабляют друг друга. В результате несложных рассуждений и вычислений можно показать, что суммарная амплитуда волны, которая приходит к приемнику, будет равна половине первой или центральной зоны Френеля.
Эту амплитуду можно увеличить, если закрыть все нечетные или все четные зоны с помощью специальной пластинки, которая называется зонной.
Дифракция волн
В пункте выше было сказано, что перекрытие определенных зон Френеля позволяет увеличивать интенсивность световой волны в точке приема. Зонная пластинка, которая для этого используется, является своего рода дифракционной решеткой со щелями в виде окружностей.
Принцип Гюйгенса-Френеля явление дифракции позволяет объяснить и математически описать. Полученные формулы для дифракции Фраунгофера и Френеля на щели, решетке, круглом отверстии и других препятствиях являются результатом применения этого принципа.

Строгое математическое решение для явления дифракции
Принцип Гюйгенса-Френеля был разработан в начале XIX века. В 60-е годы того же века Джеймс Максвелл получил свою теорию электромагнетизма. Именно ее уравнения необходимо использовать для строгого решения явления дифракции.
Что касается рассмотренного в статье принципа, то он использует ряд приближений, которые упрощают математические выкладки, и при этом позволяют получать пригодные для практического использования результаты.