Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас – атомы и молекулы – имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды – основы всего живого – тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо – птицы вьют его также в этой форме.
Данная фигура в древних помыслах культур
Круг – это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.
Издавна круг – это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в этой фигуре эквивалентны, линия круга не имеет ни начала, ни конца.
А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг – конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.

Что такое окружность
Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.
Что необходимо знать и чем уметь пользоваться, чтобы построить окружность
Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.

Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей. С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
Какими величинами характеризуется окружность
Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим радиус окружности. Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.
Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.
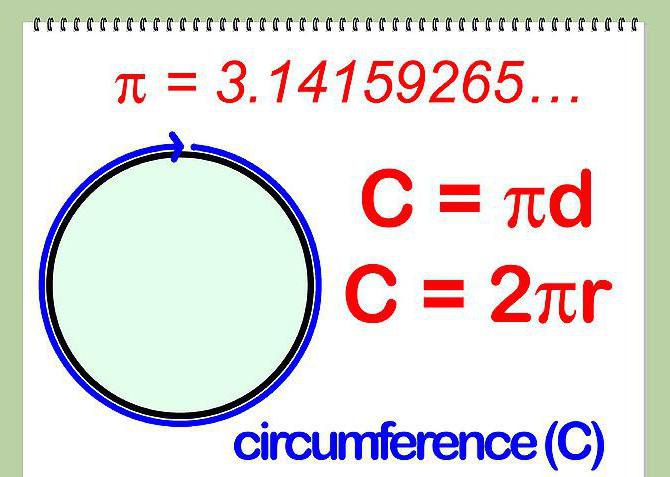
В этой формуле С – длина окружности, r – радиус окружности, d – диаметр, а число Пи – константа со значением 3,14.
Кстати, константа Пи была вычислена как раз из окружности.

Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.
В чем же главное отличие круга от окружности
По сути, окружность – это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее – это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.
Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг – это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.
Перейдем непосредственно к понятию круга
Круг – геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).
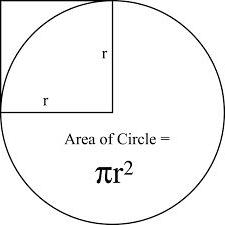
В данной формуле S – площадь, r – радиус круга. Число Пи – снова та же константа, равная 3,14.
Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.
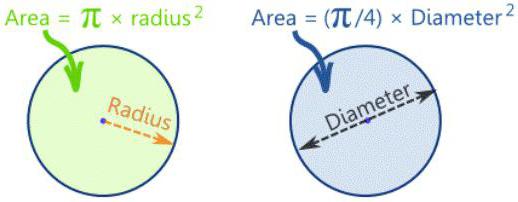
Одна четвертая появляется из того, что радиус – это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:
r*r = 1/2*d*1/2*d;
r*r = 1/4*d*d.
Круг – это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.
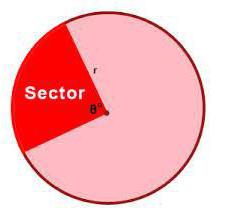
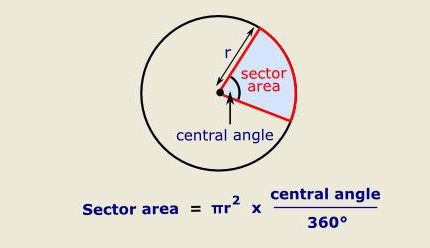
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.
Использование фигуры в задачах с многоугольниками
Также круг – геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.
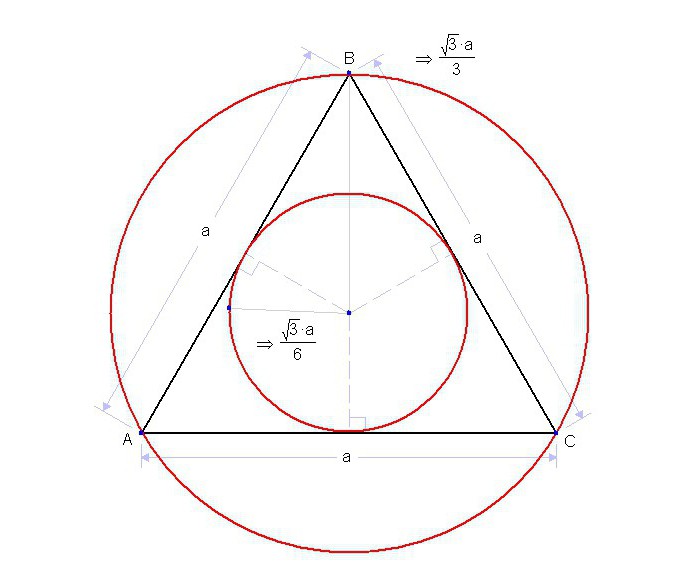
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.
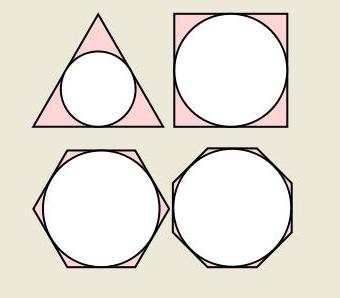
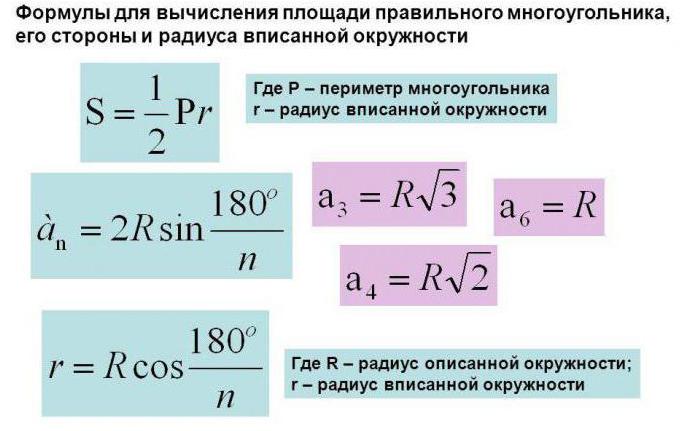
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.
Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью
Перед нами канализационный люк. Если он открыт, то железная каемка люка – это окружность. Если он закрыт, то крышка выступает в роли круга.
Окружностью также можно назвать любое кольцо – золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, – тоже окружность.
А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, –это круг.
Горлышко бутылки или банки при виде сверху – это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.
Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.


























