Дифференциальное исчисление является разделом математического анализа, который изучает производную, дифференциалы и их использование при исследовании функции.
История появления
Дифференциальное исчисление выделилось в самостоятельную дисциплину во второй половине 17 века, благодаря трудам Ньютона и Лейбница, которые сформулировали основные положения в исчислении дифференциалов и заметили связи между интегрированием и дифференцированием. С того момента дисциплина развивалась вместе с исчислением интегралов, составляя тем самым основу математического анализа. Появление данных исчислений открыло новый современный период в математическом мире и вызвало возникновение новых дисциплин в науке. Также расширило возможность применения математической науки в естествознании и технике.
Основные понятия
Дифференциальное исчисление базируется на фундаментальных понятиях математики. Ими являются: действительное число, непрерывности, функция и предел. Спустя время они приняли современный вид, благодаря интегральным и дифференциальным исчислениям.

Процесс создания
Формирование дифференциального исчисления в виде прикладного, а затем и научного метода произошло перед возникновением философской теории, которую создал Николай Кузанский. Его работы считаются эволюционным развитием из суждений античной науки. Несмотря на то что сам философ математиком не был, его вклад в развитие математической науки неоспорим. Кузанский один из первых ушел от рассмотрения арифметики как максимально точной области науки, поставив математику того времени под сомнения.
У античных математиков универсальным критерием была единица, в то время как философ предложить в качестве новой меры бесконечность взамен точного числа. В связи с этим инвертируется представление точности в математической науке. Научное знание, по его представлению, делится на рассудочное и интеллектуальное. Второе является более точным, по мнению ученого, поскольку первое дает лишь приблизительный результат.

Идея
Основная идея и понятие в дифференциальном исчислении связаны с функцией в малых окрестностях определенных точек. Для этого необходимо создать математический аппарат для исследований функции, поведение которой в малой окрестности установленных точек близко к поведению многочлена или линейной функции. Основано это на определении производной и дифференциала.
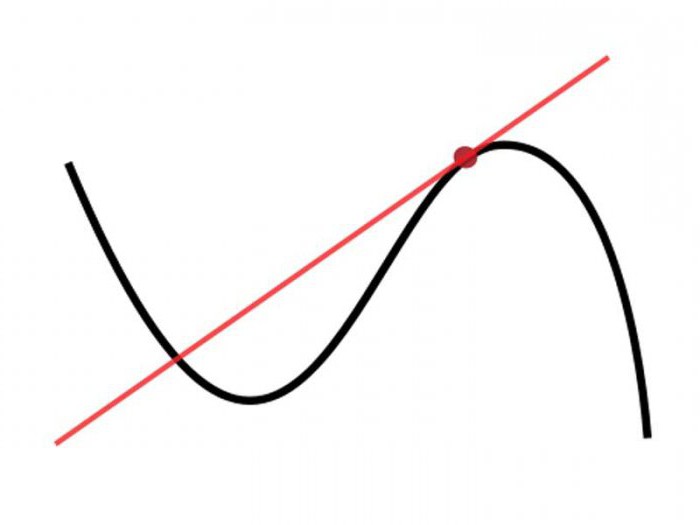
Появление понятия производной было вызвано большим число задач из естественных наук и математики, которые приводили к нахождению значений пределов одного типа.
Одной из основных задач, которые даются как пример, начиная со старших классов школы, является определение скорости движения точки по прямой линии и построение касательной линии к этой кривой. Дифференциал связан с этим, поскольку есть возможность приблизить функцию в малой окрестности рассматриваемой точки линейной функции.
По сравнению с понятием производной функции действительной переменной, определение дифференциалов просто переходит на функцию общей природы, в частности на изображение одного евклидова пространства на другое.
Производная
Пусть точка движется по направлению оси Оу, за время возьмем х, которое отсчитывается от некоего начала момента. Описать такое перемещение можно по функции у=f(x), которая ставится в соответствие каждому временному моменту х координаты перемещаемой точки. Данную функцию в механике принять звать законом движения. Основной характеристикой движения, в особенности неравномерного, является мгновенная скорость. Когда точка перемещается по оси Оу согласно закону механики, то в случайный временной момент х она приобретает координату f(x). Во временной момент х + Δх, где Δх обозначает приращение времени, ее кордината будет f(х + Δх). Так формируется формула Δy = f(х + Δх) - f(х), которую называют приращением функции. Она представляет собой пройденный точкой путь за время от х до х + Δх.
В связи с возникновением этой скорости в момент времени вводится производная. В произвольной функции производную в фиксированной точке называют пределом (при условии его существования). Обозначаться она может определенными символами:
f’(х), y’, ý, df/dx, dy/dx, Df(x).
Процесс вычисления производной именуют дифференцированием.
Дифференциальное исчисление функции нескольких переменных
Данный метод исчисления применятся при исследовании функции с несколькими переменными. При наличии двух переменных х и у, частная производная по х в точке А зовется производной этой функции по х с фиксированным у.
Может обозначаться следующими символами:
f’(x)(x,y), u’(x), ∂u/∂x или ∂f(x,y)’/∂x.
Необходимые навыки
Чтобы успешно изучить и уметь решать диффуры, требуются навыки в интегрировании и дифференцировании. Чтобы было легче разобраться в дифференциальных уравнениях, следует хорошо понимать тему производной и неопределенный интеграл. Также не помешает научиться искать производную от неявно заданной функции. Связано это с тем, что в процессе изучения придется часто использовать интегралы и дифференцирование.
Типы дифференциальных уравнений
Практически во всех контрольных работах, связанных с дифференциальными уравнениями первого порядка, существует 3 вида уравнений: однородные, с разделяющимися переменными, линейные неоднородные.
Имеются и более редкие разновидности уравнений: с полными дифференциалами, уравнения Бернулли и прочие.

Основы решения
Для начала следует вспомнить алгебраичные уравнения из школьного курса. В них содержатся переменные и числа. Для решения обычного уравнения следует найти множество чисел, удовлетворяющих заданному условию. Как правило, такие уравнения имели одни корень, и для проверки правильности следовало лишь подставить это значение на место неизвестной.
Дифференциальное уравнение схоже с этим. В общем случае такое уравнение первого порядка включает:
- Независимую переменную.
- Производную первой функции.
- Функцию или зависимую переменную.
В отдельных случаях может отсутствовать одна из неизвестных, х или у, однако это не столь важно, так как необходимо наличие первой производной, без производных высших порядков, чтобы решение и дифференциальное исчисление были верны.
Решить дифференциальное уравнение - это значит отыскать множество всех функций, подходящих заданному выражению. Подобное множеств функций часто называется общим решением ДУ.
Интегральное исчисление
Интегральное исчисление является одним из разделов математического анализа, который изучает понятие интеграла, свойства и методы его вычисления.
Зачастую вычисление интеграла встречается при вычислении площади криволинейной фигуры. Под этой площадью подразумевается предел, к которому стремится площадь вписанного в заданную фигуру многоугольника с постепенным возрастанием его стороны, при этом данные стороны могут быть выполнены менее всякого ранее указанного произвольного малого значения.
Главная идея в вычислении площади произвольной геометрической фигуры состоит в подсчёте площади прямоугольника, то есть доказательстве, что его площадь равняется произведению длины на ширину. Когда речь идет о геометрии, то все построения производятся при помощи линейки и циркуля, и тогда отношение длины к ширине является рациональным значением. При подсчете площади прямоугольного треугольника можно определить, что если отложить такой же треугольник рядом, то образуется прямоугольник. В параллелограмме площадь подсчитывается подобным, но чуть более усложненным методом, через прямоугольник и треугольник. В многоугольниках площадь считают через входящие в него треугольники.
При определении пощади произвольной кривой данный метод не подойдет. Если разбить её на единичные квадраты, то останутся незаполненные места. В этом случае пытаются использовать два покрытия, с прямоугольниками сверху и снизу, в результате те включают график функции и не включают. Важным здесь остается способ разбивания на эти прямоугольники. Также если брать разбивания все более уменьшающиеся, то площадь сверху и снизу должна сойтись на определенном значении.
Следует вернуться к способу разделения на прямоугольники. Имеется два популярных метода.
Риманом было формализовано определение интеграла, созданное Лейбницем и Ньютоном, как площади подграфика. В этом случае были рассмотрены фигуры, состоящие из некоторого числа вертикальных прямоугольников и полученные при разделении отрезка. Когда при уменьшении разбивания имеется предел, к которому сводится площадь подобной фигуры, этот предел называют интегралом Римана функции на заданном отрезке.
Вторым методом является построение интеграла Лебега, состоящее в том, что за место разделения определяемой области на части подынтегральной функции и составления затем интегральной суммы из полученных значений в этих частях, на интервалы делится её область значений, а после суммируется с соответствующими мерами прообразов этих интегралов.
Современные пособия
Одно из основных пособий по изучению дифференциального и интегрального исчисления написал Фихтенгольц - "Курс дифференциального и интегрального исчисления". Его учебник является фундаментальным пособием по изучению математического анализа, который выдержал много изданий и переводов на другие языки. Создан для студентов вузов и долгое время применяется во множестве учебных заведений как одно из основных пособий по изучению. Дает теоретические данные и практические умения. Впервые издан в 1948 году.
Алгоритм исследования функции
Чтобы исследовать методами дифференциального исчисления функцию, необходимо следовать уже заданному алгоритму:
- Найти область определения функции.
- Найти корни заданного уравнения.
- Подсчитать экстремумы. Для этого следует вычислить производную и точки, где она равняется нулю.
- Подставляем полученное значение в уравнение.
Разновидности дифференциальных уравнений
ДУ первого порядка (иначе, дифференциальное исчисление одной переменной) и их виды:
- Уравнение с разделяющимися переменными: f(y)dy=g(x)dx.
- Простейшие уравнения, или дифференциальное исчисление функции одной переменной, имеющие формулу: y'=f(x).
- Линейное неоднородное ДУ первого порядка: y'+P(x)y=Q(x).
- Дифференциальное уравнение Бернулли: y'+P(x)y=Q(x)ya .
- Уравнение с полными дифференциалами: P(x,y)dx+Q(x,y)dy=0.
Дифференциальные уравнения второго порядка и их виды:
- Линейное однородное дифференциальное уравнение второго порядка с постоянными значениями коэффициента: yn+py'+qy=0 p, q принадлежит R.
- Линейное неоднородное дифференциальное уравнение второго порядка с постоянным значением коэффициентов: yn+py'+qy=f(x).
- Линейное однородное дифференциальное уравнение: yn+p(x)y'+q(x)y=0, и неоднородное уравнение второго порядка: yn+p(x)y'+q(x)y=f(x).
Дифференциальные уравнения высших порядков и их виды:
- Дифференциальное уравнение, допускающие понижение порядка: F(x,y(k),y(k+1),..,y(n)=0.
- Линейное уравнение высшего порядка однородное: y(n)+f(n-1)y(n-1)+...+f1y'+f0y=0, и неоднородное: y(n)+f(n-1)y(n-1)+...+f1y'+f0y=f(x).
Этапы решения задачи с дифференциальным уравнением
С помощью ДУ решаются не только математические или физические вопросы, но и различные проблемы из биологии, экономики, социологии и прочего. Несмотря на большое разнообразие тем, следует придерживаться единой логической последовательности при решении подобных проблем:
- Составление ДУ. Один из наиболее сложных этапов, который требует максимальный точности, поскольку любая ошибка приведет к полностью неверным итогам. Следует учитывать все факторы, влияющие на процесс, и определить начальные условия. Также следует основываться на фактах и логических выводах.
- Решение составленного уравнения. Этот процесс проще первого пункта, поскольку требует лишь строгого выполнения математических подсчетов.
- Анализ и оценка полученных итогов. Выведенное решение следует оценить для установки практической и теоретической ценности результата.
Пример использования дифференциальных уравнений в медицине
Использование ДУ в области медицины встречается при построении эпидемиологической математической модели. При этом не стоит забывать, что данные уравнения также встречаются в биологии и химии, которые близки к медицине, потому что в ней немаловажную роль играет исследование разных биологических популяций и химических процессов в теле человека.
В приведённом примере с эпидемией можно рассматривать распространение инфекции в изолированном обществе. Обитатели подразделяются на три вида:
- Инфицированные, численность x(t), состоявшие из особей, носителей инфекции, каждый из которых заразен (инкубационный период короткий).
- Второй вид включает восприимчивых особей y(t), способных заразиться при контактировании с инфицированными.
- Третий вид включает в себя невосприимчивых особей z(t), которые имеют иммунитет или погибли из-за болезни.
Количество особей постоянно, учет рождения, естественных смертей и миграции не учитывается. В основе будет иметься две гипотезы.
Процент заболеваемости в определённый временной момент равняется x(t)y(t) (основывается предположение на теории, что число заболевших пропорционально количеству пересечений между больными и восприимчивыми представителями, которое в первом приближении будет пропорционально x(t)y(t)), в связи с этим количество заболевших возрастает, а число восприимчивых уменьшается со скоростью, которая вычисляется по формуле ax(t)y(t) (a > 0).
Число невосприимчивых особей, которые приобрели иммунитет или погибли, возрастает со скоростью, которая пропорциональна количеству заболевших, bx(t) (b > 0).
В итоге можно составить систему уравнений с учетом всех трех показателей и на её основе сделать выводы.
Пример использования в экономике
Дифференциальное исчисление часто применяется при экономическом анализе. Основной задачей в экономическом анализе считается изучение величин из экономики, которые записаны в форму функции. Это используется при решении задач вроде изменения дохода сразу после увеличения налогов, ввода пошлин, изменения выручки компании при изменении стоимости продукции, в какой пропорции можно заменить выбывших работников новым оборудованием. Чтобы решить такие вопросы, требуется построить функцию связи из входящих переменных, которые после изучаются с помощью дифференциального исчисления.
В экономической сфере часто необходимо отыскать наиболее оптимальные показатели: максимальную производительность труда, наивысший доход, наименьшие издержки и прочее. Каждый такой показатель является функцией из одного или нескольких аргументов. К примеру, производство можно рассмотреть как функцию из затраты труда и капитала. В связи с этим нахождение подходящего значения можно свести к отысканию максимума или минимума функции из одной или нескольких переменных.
Такого рода задачи создают класс экстремальных задач в экономической области, для решения которых необходимо дифференциальное исчисление. Когда экономический показатель требуется минимизировать или максимизировать как функцию от другого показателя, то в точке максимума отношение приращения функции к аргументам будет стремиться к нулю, если приращение аргумента стремится к нулевому значению. Иначе же, когда подобное отношение стремится к некому положительному или отрицательному значению, указанная точка не является подходящей, потому что при увеличении или уменьшении аргумента можно поменять зависимую величину в необходимом направлении. В терминологии дифференциального исчисления это будет значить, что требуемым условием для максимума функции является нулевое значение её производной.
В экономике нередко встречаются задачи на нахождение экстремума функции с несколькими переменными, потому что экономические показатели складываются из многих факторов. Подобные вопросы хорошо изучены в теории функций нескольких переменных, применяющей методы дифференциального вычисления. Подобные задачи включают в себя не только максимизируемые и минимизируемые функции, но и ограничения. Подобные вопросы относятся к математическому программированию, и решаются они с помощью специально разработанных методов, также опирающихся на этот раздел науки.
Среди методов дифференциального исчисления, используемых в экономике, важным разделом является предельный анализ. В экономической сфере этот термин обозначает совокупность приемов исследования изменяемых показателей и результатов при смене объемов создания, потребления, основываясь на анализе их предельных показателей. Предельным показателем считается производная или частные производные при нескольких переменных.
Дифференциальное исчисление нескольких переменных - немаловажная тема из области математического анализа. Для подробного изучения можно использовать различные учебные пособия для высших учебных заведений. Одно из наиболее известных создал Фихтенгольц - "Курс дифференциального и интегрального исчисления". Как заметно из названия, для решения дифференциальных уравнений немалое значение имеют навыки в работе с интегралами. Когда имеет место дифференциальное исчисление функции одной переменной, решение становится проще. Хотя, надо заметить, оно подчиняется тем же основным правилам. Чтобы на практике исследовать функцию дифференциальным исчислением, достаточно следовать уже имеющемуся алгоритму, который дается в старших классах школы и лишь немногим осложняется при вводе новых переменных.


























