Сейчас речь пойдет о геометрической оптике. В этом разделе много времени уделяется такому объекту, как линза. Ведь она может быть разной. При этом формула тонкой линзы одна на все случаи. Только нужно знать, как ее правильно применить.

Виды линз
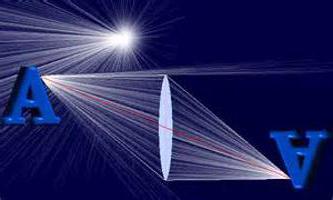
Ею всегда является прозрачное для световых лучей тело, которое имеет особенную форму. Внешний вид объекта диктуют две сферические поверхности. Одну из них допускается заменить на плоскую.
Причем у линзы может оказаться толще середина или края. В первом случае она будет называться выпуклой, во втором — вогнутой. Причем в зависимости от того, как сочетаются вогнутые, выпуклые и плоские поверхности, линзы тоже могут быть разными. А именно: двояковыпуклыми и двояковогнутыми, плосковыпуклыми и плосковогнутыми, выпукло-вогнутыми и вогнуто-выпуклыми.
В обычных условиях эти объекты используются в воздухе. Изготавливают их из вещества, оптическая плотность которого больше, чем у воздуха. Поэтому выпуклая линза будет собирающей, а вогнутая — рассеивающей.
Общие характеристики
До того, как говорить о формуле тонкой линзы, нужно определиться с основными понятиями. Их обязательно нужно знать. Поскольку к ним постоянно будут обращаться различные задачи.
Главная оптическая ось — это прямая. Она проведена через центры обеих сферических поверхностей и определяет место, где находится центр линзы. Существуют еще дополнительные оптические оси. Они проводятся через точку, являющуюся центром линзы, но не содержат центры сферических поверхностей.
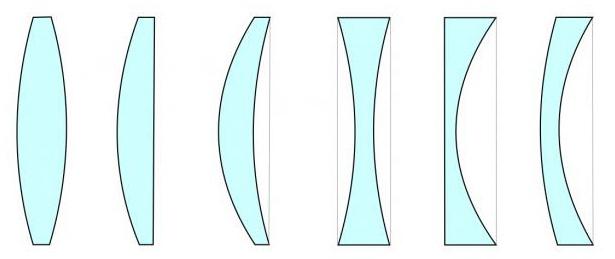
В формуле тонкой линзы есть величина, определяющая ее фокусное расстояние. Так, фокусом является точка на главной оптической оси. В ней пересекаются лучи, идущие параллельно указанной оси.
Причем фокусов у каждой тонкой линзы всегда два. Они расположены по обе стороны от ее поверхностей. Оба фокуса у собирающей действительные. У рассеивающей — мнимые.
Расстояние от линзы до точки фокуса — это фокусное расстояние (буква F). Причем его значение может быть положительным (в случае собирающей) или отрицательным (для рассеивающей).
С фокусным расстоянием связана еще одна характеристика — оптическая сила. Ее принято обозначать D. Ее значение всегда - величина, обратная фокусу, то есть D = 1/F. Измеряется оптическая сила в диоптриях (сокращенно, дптр).
Какие еще обозначения есть в формуле тонкой линзы
Помимо уже указанного фокусного расстояния, потребуется знать несколько расстояний и размеров. Для всех видов линз они одинаковые и представлены в таблице.
| Обозначение | Название |
| d | расстояние до предмета |
| h | высота изучаемого предмета |
| f | расстояние до изображения |
| H | высота получившегося изображения |
Все указанные расстояния и высоты принято измерять в метрах.
В физике с формулой тонкой линзы связано еще понятие увеличения. Оно определяется как отношение размеров изображения к высоте предмета, то есть H/h. Его можно обозначить буквой Г.
Что нужно для построения изображения в тонкой линзе
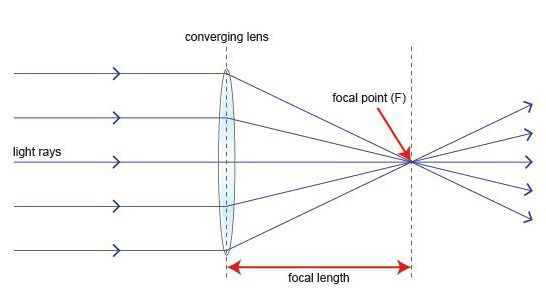
Это необходимо знать, чтобы получить формулу тонкой линзы, собирающей или рассеивающей. Чертеж начинается с того, что обе линзы имеют свое схематическое изображение. Обе они выглядят как отрезок. Только у собирающей на его концах стрелки направлены наружу, а у рассеивающей - внутрь этого отрезка.
Теперь к этому отрезку необходимо провести перпендикуляр к его середине. Так будет изображена главная оптическая ось. На ней с обеих сторон от линзы на одинаковом расстоянии полагается отметить фокусы.
Предмет, изображение которого требуется построить, рисуется в виде стрелки. Она показывает, где находится верх предмета. В общем случае предмет помещается параллельно линзе.
Как построить изображение в тонкой линзе
Для того чтобы построить изображение предмета, достаточно найти точки концов изображения, а потом их соединить. Каждая из этих двух точек может получиться от пересечения двух лучей. Наиболее простыми в построении являются два из них.
Идущий из указанной точки параллельно главной оптической оси. После соприкосновения с линзой он идет через главный фокус. Если речь идет о собирающей линзе, то этот фокус находится за линзой и луч идет через него. Когда рассматривается рассеивающая, то луч нужно провести так, чтобы его продолжение проходило через фокус перед линзой.
Идущий непосредственно через оптический центр линзы. Он не изменяет за ней своего направления.
Бывают ситуации, когда предмет поставлен перпендикулярно главной оптической оси и заканчивается на ней. Тогда достаточно построить изображение точки, которая соответствует краю стрелки, не лежащей на оси. А потом провести из нее перпендикуляр к оси. Это и будет изображение предмета.
Пересечение построенных точек дает изображение. В тонкой собирающей линзе получается действительное изображение. То есть оно получается непосредственно на пересечении лучей. Исключением является ситуация, когда предмет помещен между линзой и фокусом (как в лупе), тогда изображение оказывается мнимым. У рассеивающей же оно всегда получается мнимым. Ведь оно получается на пересечении не самих лучей, а их продолжений.
Действительное изображение принято чертить сплошной линией. А вот мнимое - пунктиром. Связано это с тем, что первое на самом деле там присутствует, а второе только видится.
Вывод формулы тонкой линзы
Это удобно сделать на основе чертежа, иллюстрирующего построение действительного изображения в собирающей линзе. Обозначение отрезков указано на чертеже.
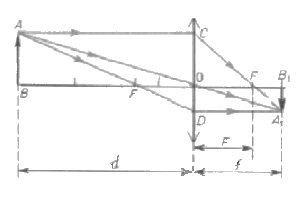
Раздел оптики не зря называется геометрической. Потребуются знания именно из этого раздела математики. Для начала необходимо рассмотреть треугольники АОВ и А1ОВ1. Они подобны, поскольку в них имеется по два равных угла (прямые и вертикальные). Из их подобия следует, что модули отрезков А1В1 и АВ относятся как модули отрезков ОВ1 и ОВ.
Подобными (на основании того же принципа по двум углам) оказываются еще два треугольника: COF и A1FB1. В них равны отношения уже таких модулей отрезков: А1В1 с СО и FB1с OF. Исходя из построения равными будут отрезки АВ и СО. Поэтому левые части указанных равенств отношений одинаковые. Поэтому равны и правые. То есть ОВ1 / ОВ равно FB1/ OF.
В указанном равенстве отрезки, обозначенные точками, можно заменить на соответствующие физические понятия. Так ОВ1 — это расстояние от линзы до изображения. ОВ является расстоянием от предмета до линзы. OF — фокусное расстояние. А отрезок FB1 равен разности расстояния до изображения и фокуса. Поэтому его можно переписать по-другому:
f / d = (f – F) / F или Ff = df – dF.
Для вывода формулы тонкой линзы последнее равенство необходимо разделить на dfF. Тогда получается:
1/ d + 1/f = 1/F.
Это у есть формула тонкой собирающей линзы. У рассеивающей фокусное расстояние отрицательное. Это приводит к изменению равенства. Правда, оно незначительное. Просто в формуле тонкой рассеивающей линзы стоит минус перед отношением 1/F. То есть:
1/ d + 1/f = - 1/F.
Задача о нахождении увеличения линзы
Условие. Фокусное расстояние собирающей линзы равно 0,26 м. Требуется вычислить ее увеличение, если предмет находится на расстоянии 30 см.
Решение. Его начать стоит с введения обозначений и перевода единиц в Си. Так, известны d = 30 см = 0,3 м и F = 0,26 м. Теперь нужно выбрать формулы, основная из них та, которая указана для увеличения, вторая — для тонкой собирающей линзы.
Их нужно как-то объединить. Для этого придется рассмотреть чертеж построения изображения в собирающей линзе. Из подобных треугольников видно, что Г = H/h= f/d. То есть для того, чтобы найти увеличение, придется вычислить отношение расстояния до изображения к расстоянию до предмета.
Второе известно. А вот расстояние до изображения полагается вывести из формулы, указанной ранее. Получается, что
f = dF / (d - F).
Теперь эти две формулы необходимо объединить.
Г = dF / (d(d - F)) = F / (d - F).
В этот момент решение задачи на формулу тонкой линзы сводится к элементарным расчетам. Осталось подставить известные величины:
Г = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Ответ: линза дает увеличение в 6,5 раз.
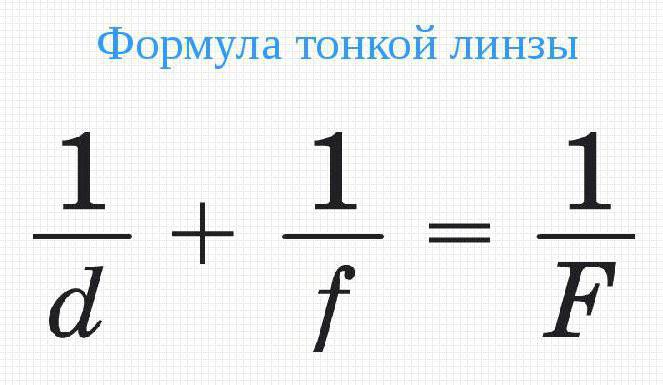
Задача, в которой нужно найти фокус
Условие. Лампа расположена в одном метре от собирающей линзы. Изображение ее спирали получается на экране, отстоящем от линзы на 25 см. Вычислите фокусное расстояние указанной линзы.
Решение. В данные полагается записать такие величины: d =1 м и f = 25 см = 0,25 м. Этих сведений достаточно, чтобы из формулы тонкой линзы вычислить фокусное расстояние.
Так 1/F = 1/1 + 1/0,25 = 1 + 4 = 5. Но в задаче требуется узнать фокус, а не оптическую силу. Поэтому остается только разделить 1 на 5, и получится фокусное расстояние:
F = 1/5 = 0,2 м.
Ответ: фокусное расстояние собирающей линзы равно 0,2 м.
Задача о нахождении расстояния до изображения
Условие. Свечку поставили на расстоянии 15 см от собирающей линзы. Ее оптическая сила равна 10 дптр. Экран за линзой поставлен так, что на нем получается четкое изображение свечи. Чему равно это расстояние?
Решение. В краткую запись полагается записать такие данные: d = 15 см = 0,15 м, D = 10 дптр. Формулу, выведенную выше, нужно записать с небольшим изменением. А именно, в правой части равенства поставить D вместо 1/F.
После нескольких преобразований получается такая формула для расстояния от линзы до изображения:
f = d / (dD - 1).
Теперь необходимо подставить все числа и сосчитать. Получается такое значение для f: 0,3 м.
Ответ: расстояние от линзы до экрана равно 0,3 м.

Задача о расстоянии между предметом и его изображением
Условие. Предмет и его изображение отстоят друг от друга на 11 см. Собирающая линза дает увеличение в 3 раза. Найти ее фокусное расстояние.
Решение. Расстояние между предметом и его изображением удобно обозначить буквой L = 72 см = 0,72 м. Увеличение Г = 3.
Здесь возможны две ситуации. Первая — предмет стоит за фокусом, то есть изображение получается действительное. Во второй — предмет между фокусом и линзой. Тогда изображение с той же стороны, что и предмет, причем мнимое.
Рассмотрим первую ситуацию. Предмет и изображение находятся по разные стороны от собирающей линзы. Здесь можно записать такую формулу: L = d + f. Вторым уравнением полагается записать: Г = f / d. Необходимо решить систему этих уравнений с двумя неизвестными. Для этого заменить L на 0,72 м, а Г на 3.
Из второго уравнения получается, что f = 3d. Тогда первое преобразуется так: 0,72 = 4d. Из него легко сосчитать d = 0,18 (м). Теперь легко определить f = 0,54 (м).
Осталось воспользоваться формулой тонкой линзы, чтобы вычислить фокусное расстояние. F = (0,18 * 0,54) / (0,18 + 0,54) = 0,135 (м). Это ответ для первого случая.
Во второй ситуации — изображение мнимое, и формула для L будет другой: L = f - d. Второе уравнение для системы будет тем же. Аналогично рассуждая, получим, что d = 0,36 (м), а f = 1,08 (м). Подобный расчет фокусного расстояния даст такой результат: 0,54 (м).
Ответ: фокусное расстояние линзы равно 0,135 м или 0,54 м.
Вместо заключения
Ход лучей в тонкой линзе — это важное практическое приложение геометрической оптики. Ведь их используют во многих приборах от простой лупы до точных микроскопов и телескопов. Поэтому знать о них необходимо.
Выведенная формула тонкой линзы позволяет решать множество задач. Причем она позволяет делать выводы о том, какое изображение дают разные виды линз. При этом достаточно знать ее фокусное расстояние и расстояние до предмета.


























