Что такое правильные дроби? Правильные и неправильные дроби

Наступает момент, когда на уроках математики учитель начинает объяснять, что такое правильные дроби. В этот момент перед учеником открывается целое множество новых задач и упражнений, для выполнения которых приходится «поднапрячься». Не все школьники понимают эту тему с первого раза, но мы попробуем объяснить всё понятным языком. Ведь на самом деле ничего сложного и страшного здесь нет.

Смысл понятия «дробь»

На каждом шагу человек встречает ситуации, в которых нужно разделять и соединять объекты и их части. Разрубаем ли мы бревно или режем торт, выбираем банк с наибольшими процентами дохода или даже смотрим на время – повсюду нас ждут правильные дроби. Это, по сути, просто доля, фрагмент – верхнее значение показывает нам, сколько кусочков у нас есть, а нижнее – сколько их требуется, чтобы получилось целое значение.

Взгляд с разных точек зрения

Прежде чем разбираться, как сделать неправильную дробь правильной, надо разобраться в более фундаментальных вопросах. А именно – о чем вообще идёт речь?

Рассмотрим пример из повседневной жизни. Возьмите пирог, разрежьте на одинаковые куски - каждый из них будет, по сути, правильной дробью, а именно – частью от некоторого целого. Что получится, если мы сложим все полученные фрагменты вместе? Один целый пирог. А что, если частей больше, чем нужно? Мы совместили куски, получив целый пирог, а ещё и лишние остались!

С математической точки зрения мы получили неправильная дробь – это когда части в сумме дают значение больше единицы. Узнать её в задаче или уравнении – легче лёгкого. Нижняя часть - знаменатель - у неё меньше, чем верхняя - числитель. А если нижнее число больше верхнего, то это правильная дробь.

Использование

Чтобы человек захотел изучать какой-то предмет или конкретную тему, он должен осознать практическую ценность новой информации. Для чего нужны правильные и неправильные дроби? Где они используются? Работать с математическими выражениями, не зная дробей, невозможно. Да и в других науках без такой информации не обойтись: ни в химии, ни в физике, ни в экономике, ни даже в социологии или политике!

Например, опросили группу людей на предмет новой кандидатуры президента страны. Кто-то проголосовал за одного, а кто-то предпочёл второго, и на экране телевизора мы увидим проценты. А что такое процент? Это правильная дробь! В данном случае - доля избирателей среди единого множества опрошенных. В общем, без дробей в этом мире – никуда. А значит, нужно их изучать.

Смешанное число

Мы уже знаем, что такое правильная дробь. А неправильная - это такая, у которой числитель больше, чем знаменатель. Получается, что у нас есть целое число и ещё некоторая дополнительная часть. Почему бы именно в таком виде всё и не записать? Это будет называться смешанным числом.

Представьте: пирог разрезан на четыре части, и в дополнение к ним у вас есть ещё одна - пятая. Если вы хотите поделиться с несколькими друзьями, то всё в порядке – вы можете просто дать каждому по кусочку. Но хранить-то пирог удобнее целиком, разве нет? Вот и в математике так же: случается, что удобнее использовать представление числа в виде неправильной дроби, а в других случаях бывает полезно выделить в них целые части – это будет называться смешанным числом.

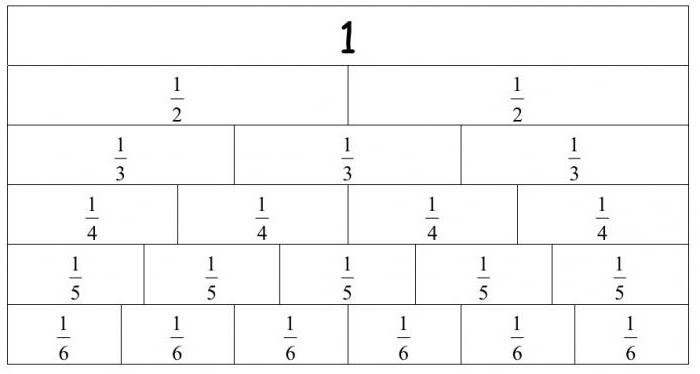
Возьмём в качестве примера 5/2. Чтобы получить смешанное число, нам нужно вычесть из числителя знаменатель столько раз, сколько он там умещается. В данном случае – два раза, и в результате мы получим две целых и одну вторую. Такое преобразование представляет собой перевод неправильной дроби в правильную. Когда вместо формулировки «три вторых» мы получаем выражение «одна целая и одна вторая», мы приходим к форме в виде смешанного числа.

Операции

С дробями можно осуществлять все те же операции, что и с целыми числами: сложение, вычитание, умножение, деление. Позже вы научитесь возводить в степень, извлекать квадратные и кубические корни, брать логарифмы. А пока надо научиться осуществлять простейшие операции с правильными и неправильными дробями.

При умножении и делении удобнее всего пользоваться не смешанными числами, а обычным представлением: только числитель и знаменатель, без целой части. Итак, у нас есть два числа и знак операции между ними – пусть это будет такое выражение: (1/2) * (2/3). А дальше все, оказывается, очень просто: мы перемножаем верхние и нижние части, а результат записываем через дробную черту: (1*2) / (2*3). Сокращаем двойки в числителе и знаменателе, получая ответ: 1/3.

При делении будет почти то же самое, только второй компонент в выражении «перевернется»: (1/2) / (2/3) = (1/2) * (3/2) = 3/4.

Сумма и разность

При сложении и вычитании можно с одинаковой легкостью использовать как смешанные числа, так и неправильные дроби (если возникает необходимость соответствующего выбора). Для этого потребуется привести слагаемые к общему знаменателю.

Как это можно сделать? Если вы помните основное свойство дроби, то знаете ответ – надо умножить обе дроби на такие числа, чтобы в нижней части у них оказались одинаковые значения. Например, есть следующие величины: 1/3 и 1/7. В соответствии с правилом, правильную дробь 1/3 умножим на 7, а 1/7 – на 3. Получим 7/21 и 3/21. Вот теперь числа можно беспрепятственно сложить: (7+3)/21 = 10/21.

Но умножать на соседний знаменатель нужно не всегда – если бы у нас была 1/4 и 1/8, проще было бы множить первое слагаемое на 2, да и дело с концом: 2/8 + 1/8 = 3/8. Точно так же происходит вычисление разности.

Ошибки

Школьники легко понимают тему неправильных и правильных дробей. Что такого сложного? Если уж ошибки и случаются, то практически всегда по невнимательности – неправильно найден общий знаменатель, например. Есть, конечно, и одна популярная ошибка, и допускается она в уравнениях.

Есть выражение: (3/4)x = 3. Требуется узнать, чему равен «икс». Ошибка может заключаться в том, что ученик осуществляет умножение обеих частей уравнения на ¾, а не деление. И тогда вместо верного ответа (x=4) получается неверный: x = 9/4. От этой проблемы избавиться легко – нужно всего лишь некоторое время не лениться записывать процедуру деления правой и левой части. Тогда ошибка сразу бросается в глаза.

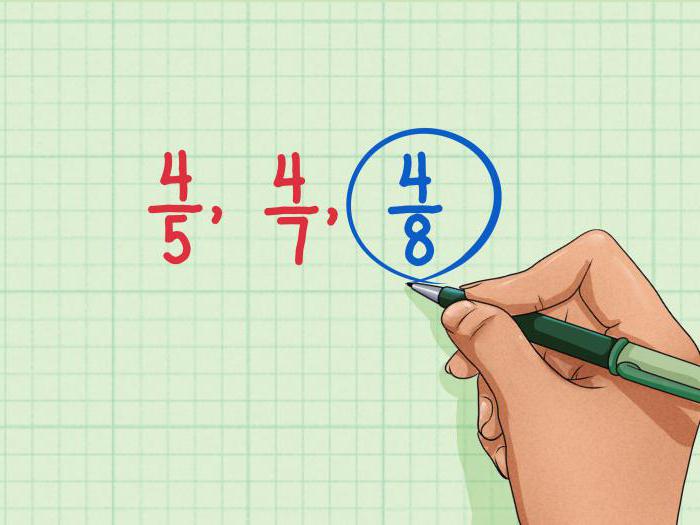
Форма записи

Записывать дроби можно вертикально, а можно – горизонтально. В первом случае получается что-то похожее на столбик, где сверху вниз мы получаем: первое число, горизонтальную черту, второе число. А если строчка узкая и «размахнуться» в высоту не получается, то можно написать эти элементы подряд, например: 1/6, 34/37. Обратите внимание, что такие правильные дроби пишутся уже с наклонной чертой. В остальном ничего существенно не изменилось.

Ещё есть десятичные дроби. Ими удобно пользоваться, но не любое число можно представить в такой форме – для этого оно должно делиться на десять без остатка, а иначе теряется точность. Посмотрите, ½ можно записать в десятичном виде, получив 0,5, а 1/3 – уже нельзя. Вернее, получится 0,333… и так до бесконечности. В математике это называется «три в периоде».

В текстовом редакторе

Можно ли записать дробь на компьютере? «Ворд» предоставляет такую возможность. Нужно всего лишь перейти в раздел «Вставка». Там вы увидите кнопку «Формула», при нажатии на которую откроется новое окошко. В нём вы сможете найти как правильные дроби, так и множество других, значительно более сложных символов – интегралы, дифференциалы, квадратные корни.

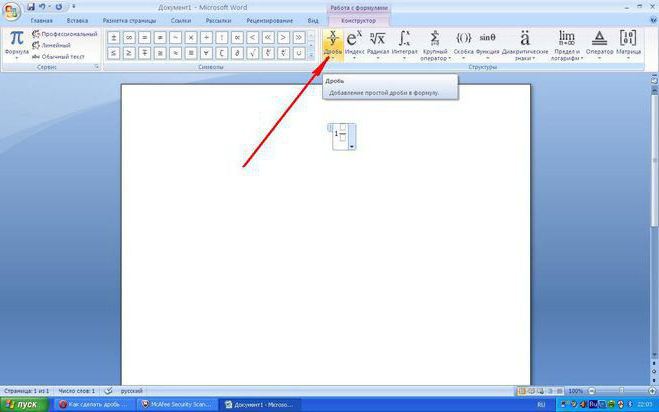
Вы пока и слов-то таких можете не знать, но однажды на математике будете проходить и их тоже. Запомните, что все эти знаки можно найти в одном месте.

В то же время в "Блокноте" такой возможности не предусмотрено. Там записывать дроби получится только в строчку, через наклонную черту.

Заключение

В любой науке важна точность. Поэтому все «кусочки» должны быть учтены, а для этого обязательно нужно понимать, как работать с правильными и неправильными дробями. Без них и самолёт не взлетит, и компьютер не включится, и блюдо по кулинарной книге приготовить не получится, и даже музыку написать не удастся. В общем, понять эту тему на уроках математики – совершенно необходимая задача, а главное - вовсе не сложная. Попрактикуйтесь, выполняя домашние задания, складывая, умножая, сравнивая дроби. Тогда вы очень быстро научитесь всё делать в уме и сможете перейти к новым интересным темам. А их в математике, уж поверьте, ещё великое множество.