Поверхности 2 порядка: примеры

С поверхностями 2-го порядка студент чаще всего встречается на первом курсе. Сначала задачи на эту тему могут казаться простыми, но, по мере изучения высшей математики и углубления в научную сторону, можно окончательно перестать ориентироваться в происходящем. Для того чтобы такого не произошло, надо не просто заучить, а понять, как получается та или иная поверхность, как изменение коэффициентов влияет на нее и ее расположение относительно изначальной системы координат и как найти новую систему (такую, в которой ее центр совпадает с началом координат, а ось симметрии параллельна одной из координатных осей). Начнем с самого начала.

Определение

Поверхностью 2 порядка называется ГМТ, координаты которого удовлетворяют общему уравнению следующего вида:

F(x,y,z)=0.

Ясно, что каждая точка, принадлежащая поверхности, должна иметь три координаты в каком-либо обозначенном базисе. Хотя в некоторых случаях геометрическое место точек может вырождаться, например, в плоскость. Это лишь значит, что одна из координат постоянна и равна нулю во всей области допустимых значений.

Полная расписанная форма упомянутого выше равенства выглядит так:

A₁₁x²+A₂₂y²+A₃₃z²+2A₁₂xy+2A₂₃yz+2A₁₃xz+2A₁₄x+2A₂₄y+2A₃₄z+A₄₄=0.

A_nm – некоторые константы, x, y, z – переменные, отвечающие аффинным координатам какой-либо точки. При этом хотя бы один из множителей-констант должен быть не равен нулю, то есть не любая точка будет отвечать уравнению.

В подавляющем большинстве примеров многие числовые множители все же тождественно равняются нулю, и уравнение значительно упрощается. На практике определение принадлежности точки к поверхности не затруднено (достаточно подставить ее координаты в уравнение и проверить, соблюдается ли тождество). Ключевым моментом в такой работе является приведение последней к каноническому виду.

Написанное выше уравнение задает любые (все указанные далее) поверхности 2 порядка. Примеры рассмотрим далее.

Виды поверхностей 2 порядка

Уравнения поверхностей 2 порядка различаются только значениями коэффициентов A_nm. Из общего вида при определенных значениях констант могут получиться различные поверхности, классифицируемые следующим образом:

1. Цилиндры.
2. Эллиптический тип.
3. Гиперболический тип.
4. Конический тип.
5. Параболический тип.
6. Плоскости.

У каждого из перечисленных видов есть естественная и мнимая форма: в мнимой форме геометрическое место вещественных точек либо вырождается в более простую фигуру, либо отсутствует вовсе.

Цилиндры

Это самый простой тип, так как относительно сложная кривая лежит только в основании, выступая в качестве направляющей. Образующими являются прямые, перпендикулярные плоскости, в которой лежит основание.

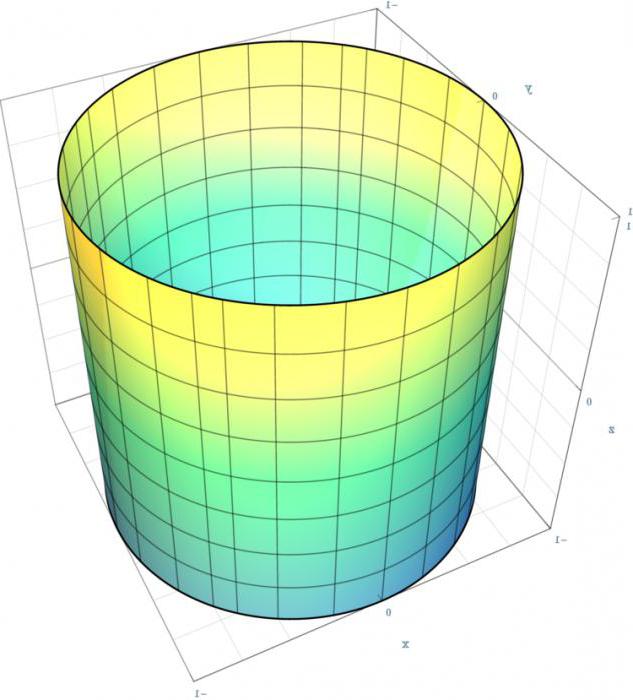
На графике показан круговой цилиндр – частный случай эллиптического цилиндра. В плоскости XY его проекция будет эллипсом (в нашем случае - кругом) - направляющей, а в XZ – прямоугольником – так как образующие параллельны оси Z. Чтобы получить его из общего уравнения, необходимо придать коэффициентам следующие значения:

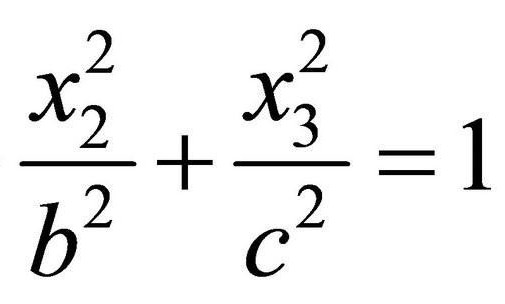
Вместо привычных обозначений икс, игрек, зет использованы иксы с порядковым номером – это не имеет никакого значения.

По сути, 1/a² и другие указанные здесь постоянные являются теми самыми коэффициентами, указанными в общем уравнении, но принято записывать их именно в таком виде – это и есть каноническое представление. Далее будет использоваться исключительно такая запись.

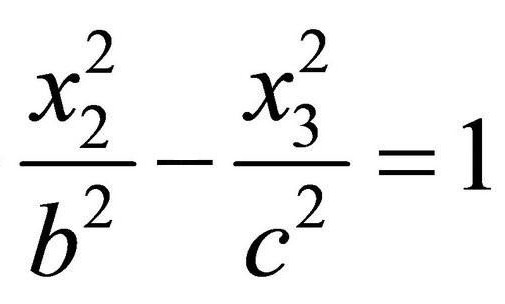
Так задается гиперболический цилиндр. Схема та же – направляющей будет гипербола.

y²=2px

Параболический цилиндр задается несколько иначе: его канонический вид включает в себя коэффициент p, называемый параметром. На самом деле, коэффициент равен q=2p, но принято разделять его на представленные два множителя.

Есть еще один вид цилиндров: мнимые. Такому цилиндру не принадлежит ни одна вещественная точка. Его описывает уравнение эллиптического цилиндра, но вместо единицы стоит -1.

Эллиптический тип

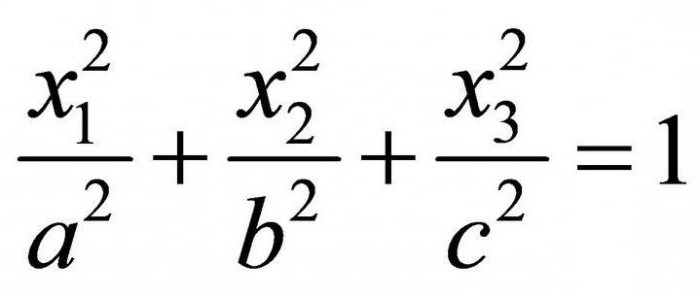
Эллипсоид может быть растянут вдоль одной из осей (вдоль которой именно зависит от значений постоянных a, b, c, указанных выше; очевидно, что большей оси будет соответствовать больший коэффициент).

Также существует и мнимый эллипсоид – при условии, что сумма координат, помноженная на коэффициенты, равна -1:

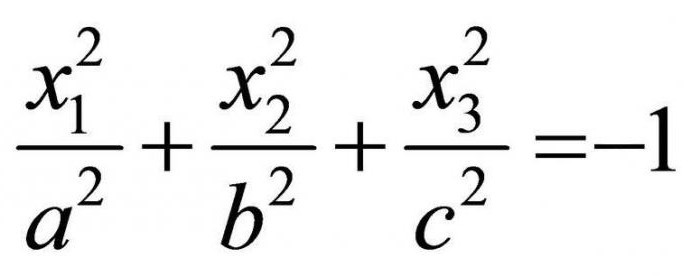
Гиперболоиды

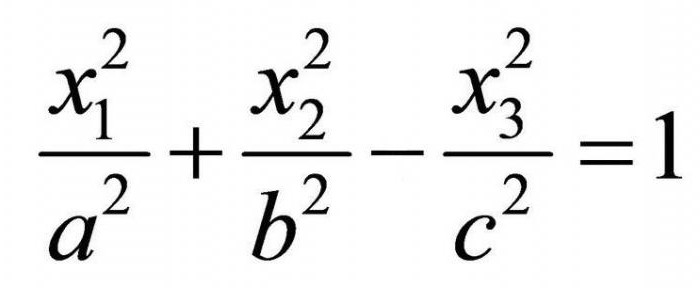
При появлении минуса в одной из констант уравнение эллипсоида превращается в уравнение однополостного гиперболоида. Надо понимать, что этот минус не обязательно должен располагаться перед координатой x₃! Он лишь определяет, какая из осей будет осью вращения гиперболоида (или параллельна ей, так как при появлении дополнительных слагаемых в квадрате (например, (x-2)²) смещается центр фигуры, как следствие, поверхность перемещается параллельно осям координат). Это относится ко всем поверхностям 2 порядка.

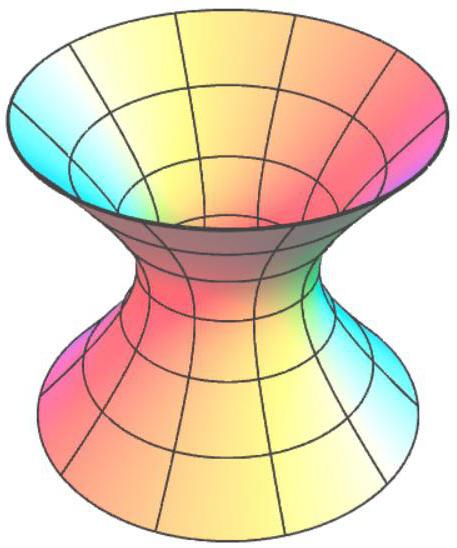
Кроме этого, надо понимать, что уравнения представлены в каноническом виде и они могут быть изменены с помощью варьирования констант (с сохранением знака!); при этом их вид (гиперболоид, конус и так далее) останется тем же.

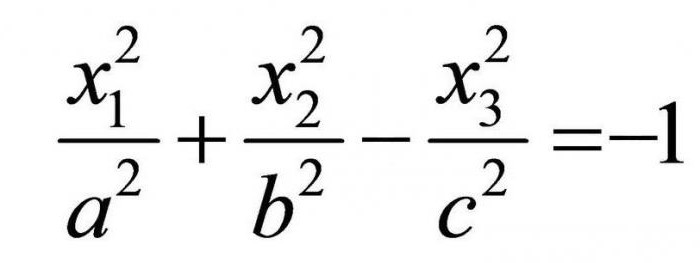
Такое уравнение задает уже двуполостный гиперболоид.

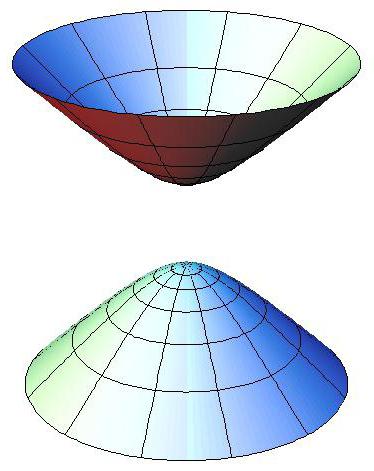
Коническая поверхность

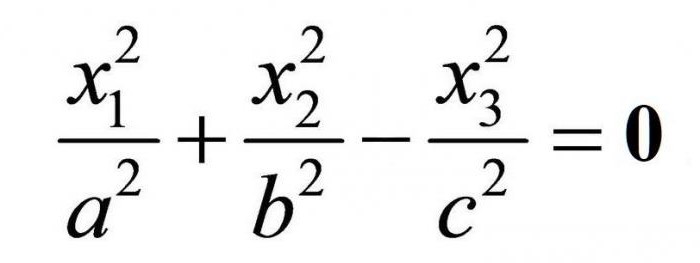
В уравнении конуса единица отсутствует – равенство нулю.

Конусом называется только ограниченная коническая поверхность. На картинке ниже видно, что, по сути, на графике окажется два так называемых конуса.

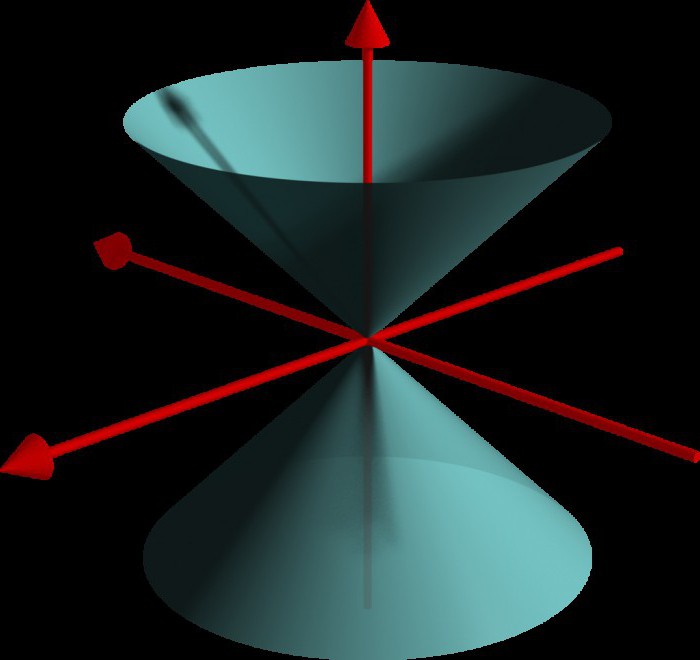
Важное замечание: во всех рассматриваемых канонических уравнениях константы по умолчанию принимаются положительными. В ином случае знак может повлиять на итоговый график.

Координатные плоскости становятся плоскостями симметрии конуса, центр симметрии располагается в начале координат.

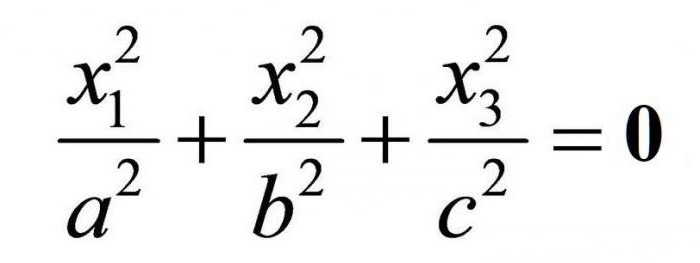
В уравнении мнимого конуса стоят только плюсы; ему принадлежит одна единственная вещественная точка.

Параболоиды

Поверхности 2 порядка в пространстве могут принимать различные формы даже при схожих уравнениях. К примеру, параболоиды бывают двух видов.

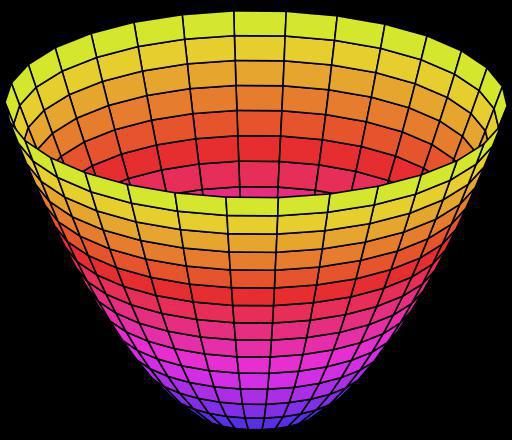
x²/a²+y²/b²=2z

Эллиптический параболоид, при расположении оси Z перпендикулярно чертежу, будет проецироваться в эллипс.

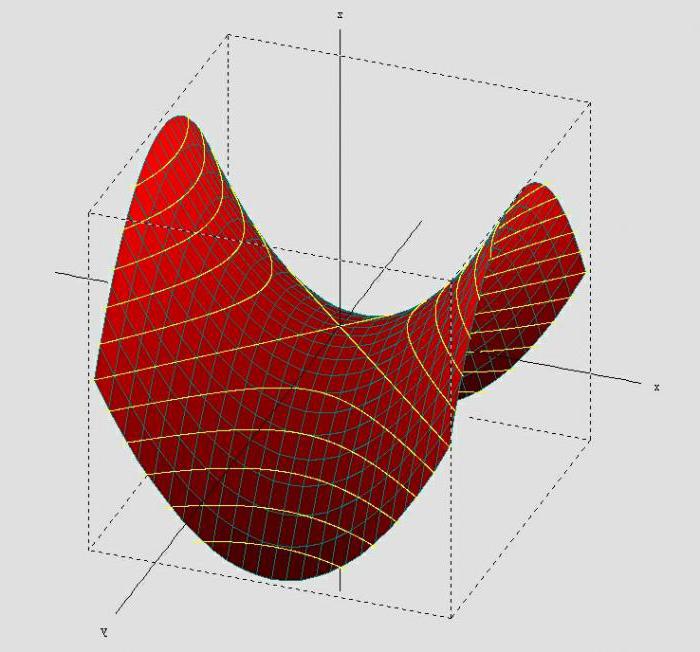
x²/a²-y²/b²=2z

Гиперболический параболоид: в сечениях плоскостями, параллельными ZY, будут получаться параболы, а в сечениях плоскостями, параллельными XY – гиперболы.

Пересекающиеся плоскости

Есть случаи, когда поверхности 2-ого порядка вырождаются в плоскости. Эти плоскости могут располагаться различными способами.

Сначала рассмотрим пересекающиеся плоскости:

x²/a²-y²/b²=0

При такой модификации канонического уравнения получаются просто две пересекающиеся плоскости (мнимые!); все вещественные точки находятся на оси той координаты, которая отсутствует в уравнении (в каноническом – оси Z).

Параллельные плоскости

y²=a²

При наличии только одной координаты поверхности 2-го порядка вырождаются в пару параллельных плоскостей. Не забывайте, на месте игрека может стоять любая другая переменная; тогда будут получаться плоскости, параллельные другим осям.

y²=−a²

В этом случае они становятся мнимыми.

Совпадающие плоскости

y²=0

При таком простом уравнении пара плоскостей вырождается в одну – они совпадают.

Не забывайте, что в случае трехмерного базиса представленное выше уравнение не задает прямую y=0! В нем отсутствуют две другие переменные, но это всего лишь значит, что их значение постоянно и равно нулю.

Построение

Одной из самых сложных задач для студента является именно построение поверхностей 2 порядка. Еще более затруднительно переходить от одной системы координат к другой, учитывая углы наклона кривой относительно осей и смещение центра. Давайте повторим, как последовательно определить будущий вид чертежа аналитическим способом.

Чтобы построить поверхность 2 порядка, необходимо:

• привести уравнение к каноническому виду;
• определить вид исследуемой поверхности;
• построить, опираясь на значения коэффициентов.

Ниже представлены все рассмотренные виды:

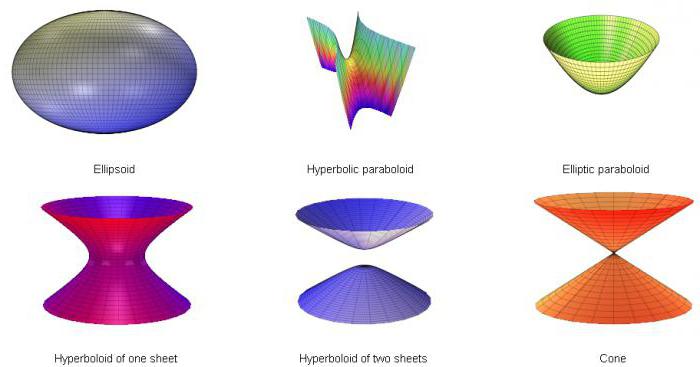
Для закрепления подробно распишем один пример такого типа задания.

Примеры

Допустим, имеется уравнение:

3(x²-2x+1)+6y²+2z²+60y+144=0

Приведем его к каноническому виду. Выделим полные квадраты, то есть скомпонуем имеющиеся слагаемые таким образом, чтобы они были разложением квадрата суммы или разности. Например: если (a+1)²=a²+2a+1, то a²+2a+1=(a+1)². Мы будем проводить вторую операцию. Скобки в данном случае раскрывать не обязательно, так как это только усложнит вычисления, а вот вынести общий множитель 6 (в скобке с полным квадратом игрека) необходимо:

3(x-1)²+6(y+5)²+2z²=6

Переменная зэт встречается в этом случае только один раз – ее можно пока не трогать.

Анализируем уравнение на данном этапе: перед всеми неизвестными стоит знак «плюс»; при делении на шесть остается единица. Следовательно, перед нами уравнение, задающее эллипсоид.

Заметьте, что 144 было разложено на 150-6, после чего -6 перенесли вправо. Почему надо было сделать именно так? Очевидно, что самый большой делитель в данном примере -6, следовательно, чтобы после деления на него справа осталась единица, необходимо «отложить» от 144 именно 6 (о том, что справа должна оказаться единица, говорит наличие свободного члена – константы, не помноженной на неизвестную).

Поделим все на шесть и получим каноническое уравнение эллипсоида:

(x-1)²/2+(y+5)²/1+z²/3=1

В использованной ранее классификации поверхностей 2 порядка рассматривается частный случай, когда центр фигуры находится в начале координат. В данном примере он смещен.

Полагаем, что каждая скобка с неизвестными – это новая переменная. То есть: a=x-1, b=y+5, c=z. В новых координатах центр эллипсоида совпадает с точкой (0,0,0), следовательно, a=b=c=0, откуда: x=1, y=-5, z=0. В изначальных координатах центр фигуры лежит в точке (1,-5,0).

Эллипсоид будет получаться из двух эллипсов: первого в плоскости XY и второго в плоскости XZ (или YZ – это не имеет значения). Коэффициенты, на которые делятся переменные, стоят в каноническом уравнении в квадрате. Следовательно, в приведенном примере правильнее было бы делить на корень из двух, единицу и корень из трех.

Меньшая ось первого эллипса, параллельная оси Y, равняется двум. Большая ось, параллельная оси X – двум корням из двух. Меньшая ось второго эллипса, параллельная оси Y, остается той же – она равна двум. А большая ось, параллельная оси Z, равняется двум корням из трех.

С помощью полученных из первоначального уравнения путем преобразования к каноническому виду данных мы можем начертить эллипсоид.

Подводя итоги

Освещенная в этой статье тема довольно обширная, но, на самом деле, как вы можете теперь видеть, не очень сложная. Ее освоение, по сути, заканчивается на том моменте, когда вы заучиваете названия и уравнения поверхностей (и, конечно, как они выглядят). В примере выше мы подробно рассматривали каждый шаг, но приведение уравнения к каноническому виду требует минимальных познаний в высшей математике и не должно вызывать никаких затруднений у студента.

Анализ будущего графика по имеющемуся равенству уже более сложная задача. Но для ее удачного решения достаточно понимать, как строятся соответствующие кривые второго порядка – эллипсы, параболы и прочие.

Случаи вырождения – еще более простой раздел. Из-за отсутствия некоторых переменных упрощаются не только вычисления, как уже было сказано ранее, но и само построение.

Как только вы сможете уверенно назвать все виды поверхностей, варьировать постоянные, превращая график в ту или иную фигуру – тема будет освоена.

Успехов в обучении!