Неинерциальная система отсчета - это... Определение и примеры

Одна из задач физики состоит в выявлении основных законов, согласно которым происходит движение материи, то есть любые изменения ее состояния во времени. Для описания движения в физике введены базовые понятия инерциальной и неинерциальной системы отсчета. Это своего рода материальная основа, опираясь на которую, можно проводить измерения характеристик состояния физической системы.

Что такое система отсчета

Любое движение возможно рассматривать только по отношению к какому-либо объекту, от параметров которого отсчитываются изменения состояния. Применительно к механическому движению в качестве такого объекта выбирают комплекс тел со строго фиксированным взаимным пространственным расположением, называемый телом отсчета, к которому привязывается система пространственных координат. В совокупности с часами, измеряющими время для этого комплекса, он и представляет собой систему отсчета. Она необязательно должна включать реальное тело – непременным условием является наличие системы координат и часов.

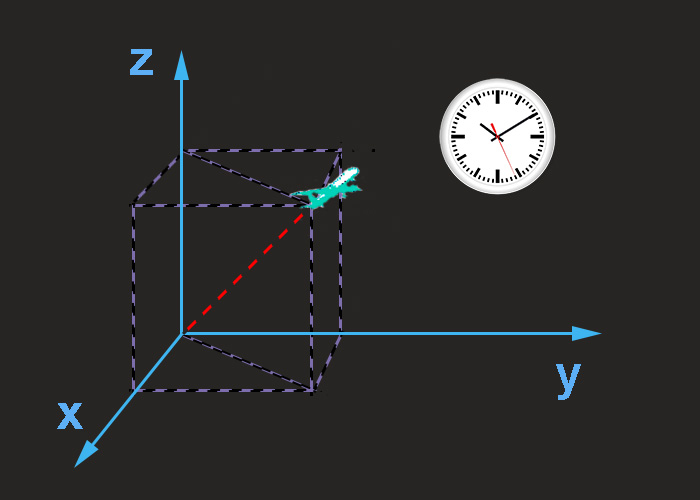
Для того чтобы разобраться в том, какие системы отсчета называются неинерциальными, необходимо обратиться к одному из фундаментальных свойств, присущих физическим телам.

Системы отсчета и инерция тела

Свойство тел сопротивляться действию сил, вызывающих ускорение, называется инерцией. С ней связан признак, по которому различают два типа систем отсчета. Инерциальной систему принято считать в том случае, если связанные с ней тела покоятся или движутся по инерции (прямолинейно и равномерно) в условиях, когда на них не воздействуют внешние силы.

Если же при отсутствии внешних сил движение тела в какой-либо системе отсчета изменяется, то эта система отсчета – неинерциальная. По отношению к некой инерциальной пространственной системе она движется ускоренно (в том числе может вращаться), а тело, связанное с ней, благодаря своей инерции стремится сохранять покой или равномерное прямое движение.

Силы инерции

Изменение движения наблюдатель зафиксирует как факт ускорения тела («материальной точки»). Поэтому на вопрос о том, какие системы отсчета называются неинерциальными, можно дать и такой ответ: это системы, в которых инерция внешне проявляет себя как источник силы, сообщающей телу ускорение.

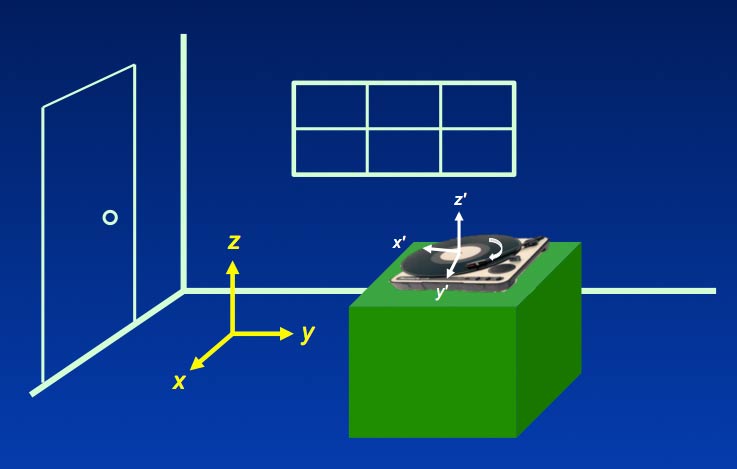
Понятие сил инерции довольно расплывчато и многозначно. Иногда их называют фиктивными, или псевдосилами, вследствие того, что их происхождение не связано с взаимодействием тел. Эти силы реальны для наблюдателя в рамках неинерциальной системы отсчета: здесь они приложены к массе тела и совершают работу. Но сторонний наблюдатель в инерциальной системе, вообще, не зафиксирует их возникновения – для него реальны будут только силы взаимодействия наблюдаемых материальных точек. Работа этих сил и вызовет изменение кинетической энергии тела.

Неинерциальные системы отсчета в классической механике

Ньютоновские законы движения были сформулированы для инерциальных систем отсчета. Однако, пользуясь ими, можно описывать движение тела и в неинерциальной системе, только при этом нужно ввести в уравнение силы инерции как реально действующие. Общий вид уравнения движения материальной точки в неинерциальной системе отсчета будет таким: ma’ = F + F_in. Здесь m – масса тела, a’ – ускорение в неинерциальной системе, F – результирующая реальных сил взаимодействия, F_in – силы инерции.

Для ясности изложенного необходимо привести несколько примеров неинерциальных систем отсчета и действующих в них сил. Во всех случаях в целях упрощения трение и сила тяжести не учитываются.

Поступательное ускорение системы отсчета

Пусть на последней открытой платформе поезда лежит незакрепленная бочка. Когда состав тронется и начнет разгоняться, бочка покатится по платформе и упадет на рельсы. Что отметит наблюдатель в инерциальной системе отсчета, стоящий на перроне (кроме факта бесхозяйственности)? Он увидит, что поезд поехал с некоторым ускорением и просто «выехал» из-под бочки, которая в системе отсчета этого наблюдателя находилась в покое.

Наблюдатель, уезжающий вместе с поездом, отметит, что без видимых причин незакрепленный предмет приобрел ускорение –a_in в направлении, противоположном ускорению состава. Поскольку оно не равно нулю, то для соблюдения законов механики наблюдателю на платформе придется предположить, что на бочку подействовала некая особая сила F_in = –ma_in. Это и будет сила инерции. Заметим, что проявляется она для этого наблюдателя как внешняя сила притяжения. Он и сам ощутит, как при разгоне поезда нечто тянет его «назад».

Центробежная сила

Теперь представим тот же состав, движущийся равномерно и входящий в поворот. В данном примере неинерциальной системы отсчета человек, едущий на платформе, немедленно ощутит, что некая сила (очевидно, вновь инерционная) смещает его к внешнему краю платформы. Величина этой силы F_in = mw²R = mv²/R (w – угловая скорость, R – радиус поворота) пропорциональна, как видим, массе пассажира и квадрату скорости состава. Направлена она радиально от центра поворота.

А вот наблюдатель, стоящий возле насыпи, увидит, что человек на платформе стремится сохранить инерционное движение, а поезд – опять-таки «выехать» из-под него. Пусть, чтобы не улететь с платформы, пассажир опирается на какой-нибудь закрепленный груз. Тогда этот груз давит на него с силой F = mv²/R, сообщающей центростремительное ускорение, позволяющее остаться в поезде. Так что и в этом случае наблюдатель, связанный с инерциальной системой отсчета, не зафиксирует никаких сил инерции.

Сила Кориолиса

Если тело движется во вращающейся пространственной системе, возникает еще одна инерционная сила – кориолисова, отклоняющая его траекторию в плоскости, ориентированной перпендикулярно к оси вращения системы. В случае приближения к этой оси сила Кориолиса отклоняет тело в направлении вращения, при удалении от оси направление действия силы противоположно вращению. В общем случае она равна векторному произведению линейной и угловой скоростей тела, умноженному на его удвоенную массу: F_in = F_K = 2m [v × w].

Так, в системе отсчета Земли из-за ее вращения тела, связанные с ней, испытывают действие силы Кориолиса. В северном полушарии она отклоняет вправо траектории полета снарядов, движение рек, колебание маятников, течения в океанах и перемещение воздушных масс. В южном полушарии смещение происходит, соответственно, влево. Проявление силы Кориолиса минимально вблизи экватора и растет с приближением к полюсам, поскольку там поверхность планеты приближается к плоскости, перпендикулярной оси ее вращения.

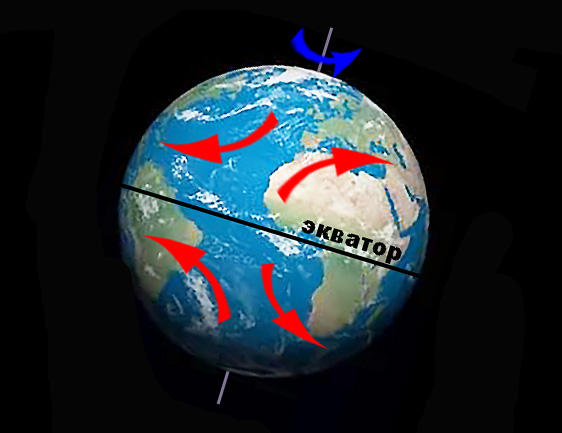
В инерциальной системе отсчета эта сила опять-таки не наблюдается. Например, маятник Фуко для такого наблюдателя сохраняет плоскость колебаний, а Земля, напротив, «проворачивается» под ним.

Масса, инерция и тяготение

Ньютоновские законы движения оперируют массой как мерой, характеризующей инертность тела, в то время как в законе всемирного тяготения фигурирует масса гравитационная. Совместное применение этих законов возможно только благодаря равенству двух видов масс, которое в рамках классической физики не находит объяснения, а является лишь наблюдательным фактом.

Несколько выше было отмечено, что поведение материальных точек в неинерциальной системе отсчета – это процесс, локально неотличимый от проявления поля гравитации, наложенного извне на инерциальную систему. Данный факт был сформулирован А. Эйнштейном в 1913 г. как принцип эквивалентности сил инерции и тяготения, означающий единство их физической природы, что позволило обобщить и понятие массы. Спустя несколько лет Эйнштейн использовал его уже при создании целостной теории.

Неинерциальные системы отсчета в общей теории относительности

Эйнштейновская теория гравитации дает возможность объяснить характер действия гравитационных сил через изменения геометрии пространственно-временного континуума в присутствии массы. Любое тело в собственной системе отсчета движется инерционно по так называемым геодезическим, или прямейшим (но не прямым!) линиям, проходящим через точки одинаковой кривизны пространства-времени.

Например, камень в падении по инерции следует по геодезической линии в деформированном массой Земли пространстве-времени. Лежащий же предмет испытывает действие силы со стороны поверхности планеты, и его пространственно-временная траектория – мировая линия – отклонена от прямейшей.

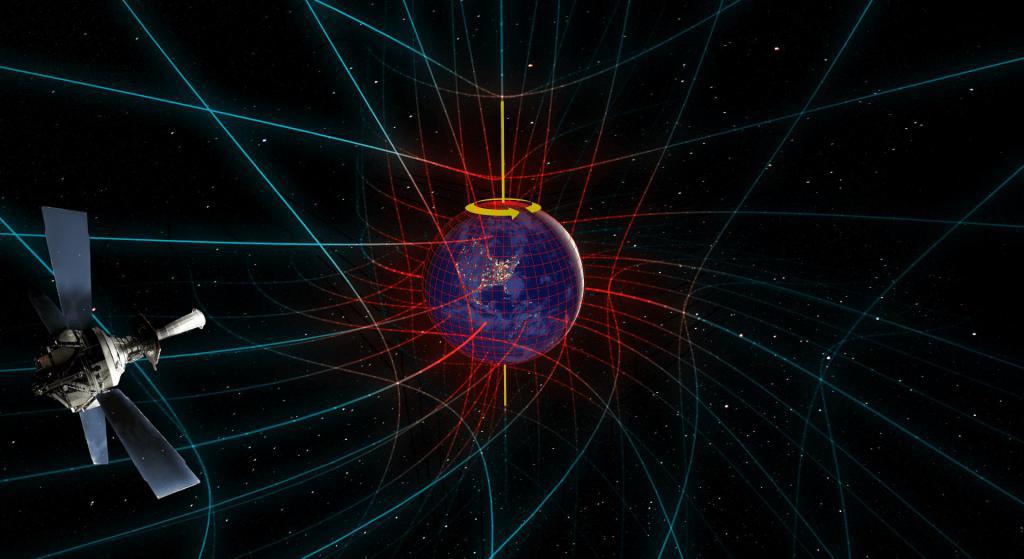
Из-за этой неравномерной и непостоянной кривизны в четырехмерном континууме нельзя выделить никакой привилегированной инерциальной системы отсчета. В реальности все они – неинерциальные и равноправные: законы физики, выраженные математическим аппаратом данной теории, не меняют вида при любых переходах между системами отсчета, то есть инвариантны относительно всех систем.

Системы отсчета в квантовом мире

Энергетическое состояние квантовых полей связано зависимостями с координатами или временем, и теоретически движение, связанное с неинерциальной системой отсчета, в квантовой теории также должно иметь особенности. Так, одно из следствий квантовой теории поля, выведенное в 1976 г. канадским физиком Б. Унру, предполагает изменение наблюдаемых свойств вакуума при движении с ускорением.

Вакуум – низшее, нулевое состояние квантового поля. В соответствии с принципом неопределенности он подвержен флуктуациям – нулевым колебаниям, которые при инерциальном движении нельзя увидеть. Однако в ускоряющейся системе отсчета наблюдатель обнаружит не нулевое состояние вакуума, а фон частиц, имеющий вид излучения с тепловым спектром.

Предсказываемое в эффекте Унру повышение температуры вакуума зависит от ускорения и составляет очень малую величину с коэффициентом порядка 10^-21 K, что чрезвычайно затрудняет возможность экспериментальной проверки. А она весьма желательна для физиков, поскольку дала бы им инструмент для определения абсолютного ускорения.

О важности понятия системы отсчета

Бесспорно, что как инерциальные, так и неинерциальные системы отсчета – это самая основа понимания сущности физического движения. Без них не обойтись ни в классической механике, прекрасно справляющейся с описанием близкого нам по масштабам мира, ни в теории относительности, раскрывающей природу пространства-времени и движения в нем, ни даже в физике квантовых систем. Даже поверхностное знакомство с ними убедительно свидетельствует о том, что мир устроен существенно сложнее, чем иногда подсказывают нам интуитивные представления, ограниченные рамками непосредственного опыта.