В математике суммирование (обозначается большим символом греческой сигмы) является набором слагаемых чисел. Что такое сумма? Это и есть результат такого действия. Если числа добавляются одно за другим слева направо, тогда промежуточный результат представляет собой частичную сумму.
Что такое сумма?
Числа, которые должны быть суммированы, могут быть целыми, рациональными, действительными или комплексными. Помимо них могут быть добавлены и другие типы значений: векторы, матрицы, многочлены и вообще элементы любой аддитивной группы (или даже моноида).
Если количество элементов слагаемых конечно, то суммирование всегда дает четко определенное значение. Суммирование бесконечной последовательности значений называется рядом. Его величина часто может быть определена с помощью предела (хотя иногда значение может быть бесконечным).
Последовательности
Суммирование чисел [3, 7, 2 ,1] можно определить выражением, значение которого представляет собой сумму цифр, входящих в него, например 3 + 7 + 2 + 1 = 13. Поскольку добавление ассоциативно, сумма не зависит от того, как сгруппированы слагаемые, например, (3 + 7) + (2+ 1) и 3 + ((7 + 2) + 1) оба равны девяти, поэтому обычно обходятся без скобок. Сложение также коммутативно, поэтому перестановка членов не меняет значение суммы. Стоит заметить, что для бесконечного суммирования это свойство может не работать.

Нет никаких специальных обозначений для суммирования последовательностей такого вида. Существует лишь небольшой нюанс, если имеется менее двух элементов. Запись суммирования последовательности одного члена не содержит знака плюса (она неотличима от вида самого числа), а если элементов и вовсе нет, то она даже не может быть записана (но вместо этого можно обозначит ее значение "0"). Если, однако, члены последовательности задаются определенным шаблоном, например функцией, то оператор суммирования может быть полезным или даже существенным.
Запись
Для понимания, что такое сумма, также необходимо разобрать ее внешний вид.
Для суммирования последовательности целых чисел от 1 до 100 часто используют выражение, включающее многоточие, чтобы указать отсутствующие члены: 1 + 2 + 3 + 4 + ... + 99 + 100. Шаблон довольно легко проглядывается в данном примере. Однако для более сложных вариантов необходимо точно указать правило, используемое для поиска величины элементов, что может быть достигнуто с помощью оператора суммирования "Σ". Используя этот символ (сигма), можно применить запись следующего вида:
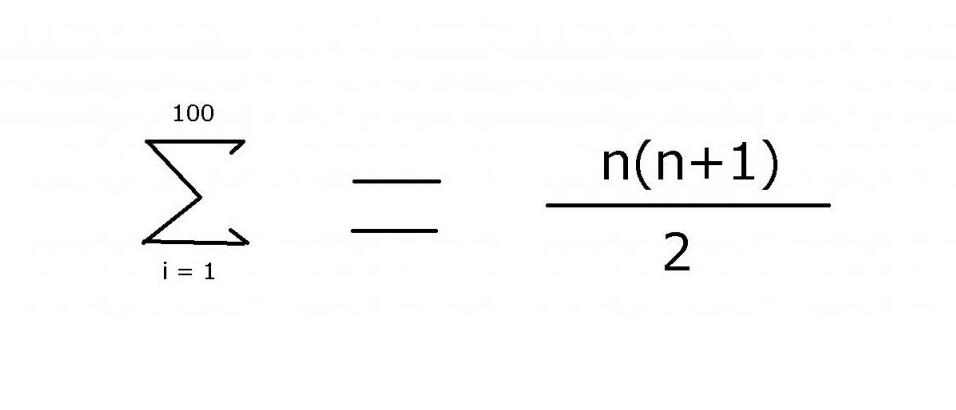
Значение этого выражения равно 5050. Его можно найти, воспользовавшись математической индукцией, откуда и взялась вторая часть формулы.
Для разных последовательностей формула будет видоизменяться. Процесс записи сводится к поиску прообраза некоторой бесконечной последовательности и последующим описанием его формулой. Сделав это, несложно понять, что такое сумма в конкретном случае.
Когда необходимо уточнить, что числа добавляются вместе с их знаками (плюс или минус), используется термин алгебраическая сумма. Например, в теории электрических цепей законы цепи Кирхгофа рассматривают алгебраическую сумму токов в сети проводников, встречающихся в точке, задавая противоположные знаки токам, текущим в и из узла.























