Квадратные уравнения часто появляются в ряде задач по математике и физике, поэтому уметь их решать должен каждый школьник. В этой статье подробно рассматриваются основные методы решения уравнений квадратных, а также приводятся примеры их использования.
Какое уравнение называется квадратным
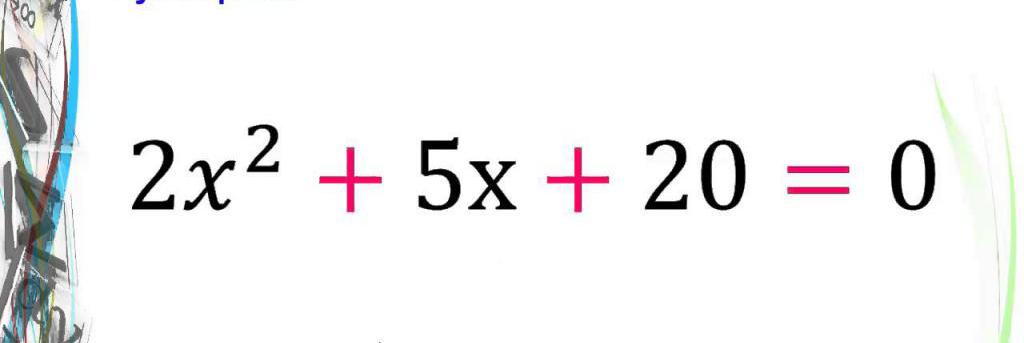
В первую очередь ответим на вопрос этого пункта, чтобы лучше понимать, о чем пойдет речь в статье. Итак, уравнение квадратное имеет следующий общий вид: c + b*x+a*x2=0, где a, b, c - некоторые числа, которые называются коэффициентами. Здесь a≠0 - это обязательное условие, в противном случае указанное уравнение вырождается в линейное. Остальные коэффициенты (b, c) могут принимать абсолютно любые значения, включая ноль. Так, выражения типа a*x2=0, где b=0 и c=0 или c+a*x2=0,где b=0, или b*x+a*x2=0, где c=0 - это тоже уравнения квадратные, которые называют неполными, поскольку в них либо линейный коэффициент b равен нулю, либо нулевым является свободный член c, либо они оба зануляются.
Уравнение, в котором a=1, называют приведенным, то есть оно вид имеет: x2 + с/a + (b/a)*x =0.
Решение квадратного уравнения заключается в нахождении таких значений x, которые удовлетворяют его равенству. Эти значения называются корнями. Поскольку рассматриваемое уравнение - это выражение второй степени, то это означает, что максимальное число его корней не может превышать двух.
Какие методы решения уравнений квадратных существуют
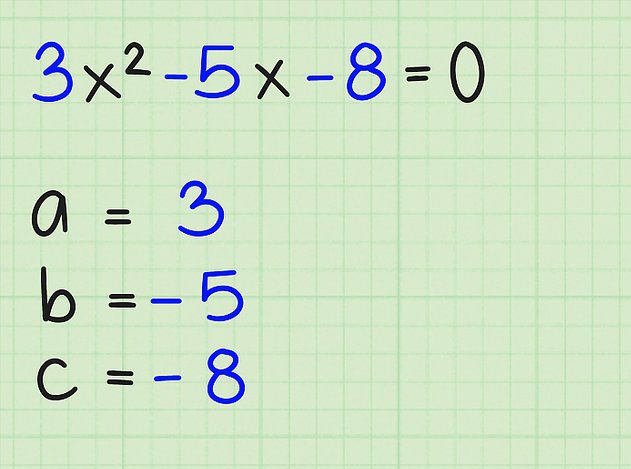
В общем случае существует 4 метода решения. Ниже перечисляются их названия:
- Разложение на множители.
- Дополнение до квадрата.
- Использование известной формулы (через дискриминант).
- Способ решения геометрический.
Как понятно из приведенного списка, первые три метода являются алгебраическими, поэтому они используются чаще, чем последний, который предполагает построение графика функции.
Существует еще один способ решения по теореме Виета уравнений квадратных. Его можно было бы включить 5-м в список выше, однако, это не сделано, поскольку теорема Виета является простым следствием 3-го метода.
Далее в статье рассмотрим подробнее названные способы решения, а также приведем примеры их использования для нахождения корней конкретных уравнений.
Метод №1. Разложение на множители
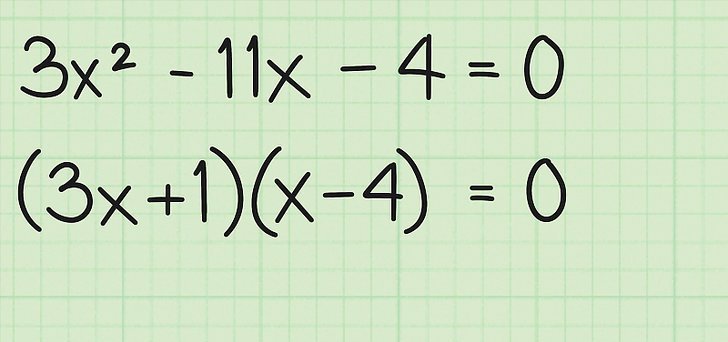
Для этого метода в математике квадратных уравнений существует красивое название: факторизация. Суть этого способа заключается в следующем: необходимо квадратное уравнение представить в виде произведения двух членов (выражений), которое должно равняться нулю. После такого представления можно воспользоваться свойством произведения, которое будет равно нулю только тогда, когда один или несколько (все) его членов являются нулевыми.
Теперь рассмотрим последовательность конкретных действий, которые нужно выполнить, чтобы найти корни уравнения:
- Перебросить все члены в одну часть выражения (например, в левую) так, чтобы в другой его части (правой) остался только 0.
- Представить сумму членов в одной части равенства в виде произведения двух линейных уравнений.
- Приравнять каждое из линейных выражений к нулю и решить их.
Как видно, алгоритм факторизации является достаточно простым, тем не менее, у большинства школьников возникают трудности во время реализации 2-го пункта, поэтому поясним его подробнее.
Чтобы догадаться, какие 2-а линейных выражения при умножении их друг на друга дадут искомое квадратное уравнение, необходимо запомнить два простых правила:
- Линейные коэффициенты двух линейных выражений при умножении их друг на друга должны давать первый коэффициент квадратного уравнения, то есть число a.
- Свободные члены линейных выражений при их произведении должны давать число c искомого уравнения.
После того, как подобраны все числа множителей, следует выполнить их перемножение, и если они дают искомое уравнение, тогда переходить к пункту 3 в изложенном выше алгоритме, в противном случае следует изменить множители, но делать это нужно так, чтобы приведенные правила всегда выполнялись.
Пример решения методом факторизации
Покажем наглядно, как алгоритм решения уравнения квадратного составить и найти неизвестные корни. Пусть дано произвольное выражение, например, 2*x-5+5*x2-2*x2 = x2+2+x2+1. Перейдем к его решению, соблюдая последовательность пунктов от 1-го до 3-х, которые изложены в предыдущем пункте статьи.
Пункт 1. Перенесем все члены в левую часть и выстроим их в классической последовательности для квадратного уравнения. Имеем следующее равенство: 2*x+(-8)+x2=0.
Пункт 2. Разбиваем на произведение линейных уравнений. Поскольку a=1, а с=-8, то подберем, например, такое произведение (x-2)*(x+4). Оно удовлетворяет изложенным в пункте выше правилам поиска предполагаемых множителей. Если раскрыть скобки, то получим: -8+2*x+x2, то есть получается точно такое же выражение, как в левой части уравнения. Это означает, что мы правильно угадали множители, и можно переходить к 3-му пункту алгоритма.
Пункт 3. Приравниваем каждый множитель нулю, получаем: x=-4 и x=2.
Если возникают какие-либо сомнения в полученном результате, то рекомендуется выполнить проверку, подставляя найденные корни в исходное уравнение. В данном случае имеем: 2*2+22-8=0 и 2*(-4)+(-4)2-8=0. Корни найдены правильно.
Таким образом, методом факторизации мы нашли, что заданное уравнение два корня различных имеет: 2 и -4.
Метод №2. Дополнение до полного квадрата
В алгебре уравнений квадратных метод множителей не всегда может использоваться, поскольку в случае дробных значений коэффициентов квадратного уравнения возникают сложности в реализации пункта 2 алгоритма.
Метод полного квадрата, в свою очередь, является универсальным и может применяться для квадратных уравнений любого типа. Суть его заключается в выполнении следующих операций:
- Члены уравнения, содержащие коэффициенты a и b, необходимо перебросить в одну часть равенства, а свободный член c - в другую.
- Далее, следует части равенства (правую и левую) разделить на коэффициент a, то есть представить уравнение в приведенном виде (a=1).
- Сумму членов с коэффициентами a и b представить в виде квадрата линейного уравнения. Поскольку a=1, то линейный коэффициент будет равен 1, что касается свободного члена уравнения линейного, то он равен должен быть половине линейного коэффициента приведенного уравнения квадратного. После того, как составлен квадрат линейного выражения, необходимо в правую часть равенства, где находится свободный член, добавить соответствующее число, которое получается при раскрытии квадрата.
- Взять квадратный корень со знаками "+" и "-" и решить полученное уже уравнение линейное.
Описанный алгоритм может на первый взгляд быть воспринят, как достаточно сложный, однако, на практике его реализовать проще, чем метод факторизации.
Пример решения с помощью дополнения до полного квадрата
Приведем пример уравнения квадратного для тренировки его решения методом изложенным в предыдущем пункте. Пусть дано уравнение квадратное -10 - 6*x+5*x2 = 0. Начинаем решать его, следуя описанному выше алгоритму.
Пункт 1. Используем метод переброски при решении уравнений квадратных, получаем: - 6*x+5*x2 = 10.
Пункт 2. Приведенный вид этого уравнения получается путем деления на число 5 каждого его члена (если равенства обе части поделить или умножить на одинаковое число, то равенство сохранится). В результате преобразований получим: x2 - 6/5*x = 2.
Пункт 3. Половина от коэффициента - 6/5 равна -6/10 = -3/5, используем это число для составления полного квадрата, получаем: (-3/5+x)2. Раскроем его и полученный свободный член следует вычесть из части равенства левой, чтобы удовлетворить исходному виду квадратного уравнения, что эквивалентно его добавлению в правую часть. В итоге получаем: (-3/5+x)2 = 59/25.
Пункт 4. Вычисляем квадратный корень с положительным и отрицательным знаками и находим корни: x = 3/5±√59/5 = (3±√59)/5. Два найденных корня имеют значения: x1 = (√59+3)/5 и x1 = (3-√59)/5.
Поскольку проведенные вычисления связаны с корнями, то велика вероятность допустить ошибку. Поэтому рекомендуется проверить правильность корней x2 и x1. Получаем для x1: 5*((3+√59)/5)2-6*(3+√59)/5 - 10 = (9+59+6*√59)/5 - 18/5 - 6*√59/5-10 = 68/5-68/5 = 0. Подставляем теперь x2: 5*((3-√59)/5)2-6*(3-√59)/5 - 10 = (9+59-6*√59)/5 - 18/5 + 6*√59/5-10 = 68/5-68/5 = 0.
Таким образом, мы показали, что найденные корни уравнения являются истинными.
Метод №3. Применение известной формулы

Этот метод решения уравнений квадратных является, пожалуй, самым простым, поскольку он заключается в подставлении коэффициентов в известную формулу. Для его использования не нужно задумываться о составлении алгоритмов решения, достаточно запомнить только одну формулу. Она приведена на рисунке выше.
В этой формуле подкоренное выражение (b2-4*a*c) называется дискриминантом (D). От его значения зависит то, какие корни получатся. Возможны 3-и случая:
- D>0, тогда уравнение корня два имеет действительных и разных.
- D=0, тогда получается корень один, который можно вычислить из выражения x = -b/(a*2).
- D<0, тогда получается два различных мнимых корня, которые представляются в виде комплексных чисел. Например, число 3-5*i является комплексным, при этом мнимая единица i удовлетворяет свойству: i2=-1.
Пример решения через вычисление дискриминанта

Приведем пример уравнения квадратного для тренировки использования приведенной выше формулы. Найдем корни для -3*x2-6+3*x+4*x = 0. Для начала вычислим значение дискриминанта, получаем: D = b2-4*a*c = 72-4*(-3)*(-6) = -23.
Поскольку получен D<0, значит, корни рассматриваемого уравнения являются числами комплексными. Найдем их, подставив найденное значение D в приведенную в предыдущем пункте формулу (она также представлена на фото выше). Получим: x = 7/6±√(-23)/(-6) = (7±i*√23)/6.
Метод №4. Использование графика функции
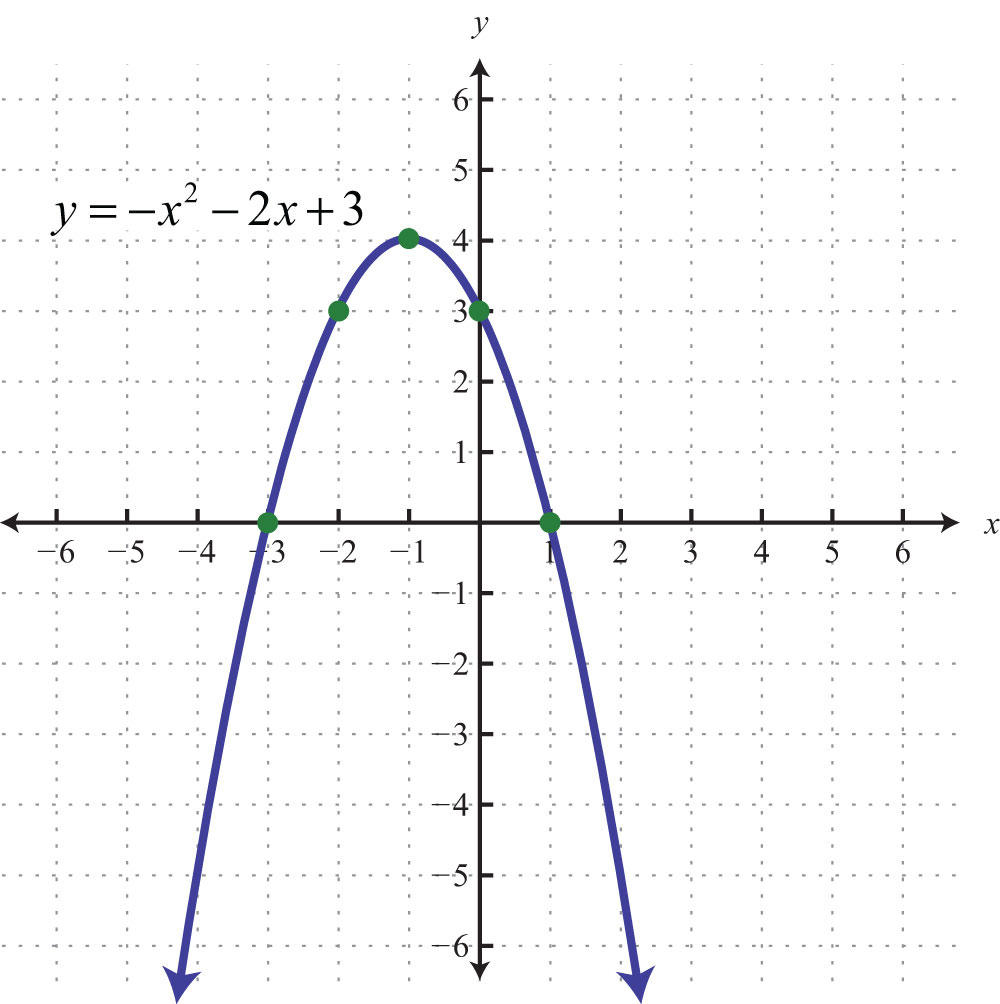
Он также называется графическим методом решения уравнений квадратных. Следует сказать, что применяется он, как правило, не для количественного, а для качественного анализа рассматриваемого уравнения.
Суть метода заключается в построении графика функции квадратичной y = f(x), который представляет собой параболу. Затем, необходимо определить, в каких точках пересекает ось абсцисс (X) парабола, они и будут корнями соответствующего уравнения.
Чтобы сказать, будет ли парабола пересекать ось X, достаточно знать положение ее минимума (максимума) и направление ее ветвей (они могут либо возрастать, либо убывать). Следует запомнить два свойства этой кривой:
- Если a>0 - параболы ветви направлены вверх, наоборот, если a<0, то они идут вниз.
- Координата минимума (максимума) параболы всегда равна x = -b/(2*a).
Например, необходимо определить, имеет ли корни уравнение -4*x+5*x2+10 = 0. Соответствующая парабола будет направлена вверх, поскольку a=5>0. Ее экстремум имеет координаты: x=4/10=2/5, y=-4*2/5+5*(2/5)2+10 = 9,2. Поскольку минимум кривой лежит над осью абсцисс (y=9,2), то она не пересекает последнюю ни при каких значениях x. То есть действительных корней приведенное уравнение не имеет.

Теорема Виета
Как выше было отмечено, эта теорема является следствием метода №3, который основан на применении формулы с дискриминантом. Суть теоремы Виета заключается в том, что она позволяет связать в равенство коэффициенты уравнения и его корни. Получим соответствующие равенства.
Воспользуемся формулой для вычисления корней через дискриминант. Сложим два корня, получаем: x1+x2 = -b/a. Теперь умножим корни друг на друга: x1*x2, после ряда упрощений получается число c/a.
Таким образом, для решения уравнений квадратных по теореме Виета можно использовать полученных два равенства. Если все три коэффициента уравнения известны, тогда корни можно найти путем решения соответствующей системы из этих двух уравнений.
Пример использования теоремы Виета
Необходимо составить квадратное уравнение, если известно, что оно имеет вид x2+c = -b*x и корни его равны 3 и -4.
Поскольку в рассматриваемом уравнении a=1, то формулы Виета будут иметь вид: x2+x1 =-b и x2*x1= с. Подставляя известные значения корней, получаем: b = 1 и c = -12. В итоге восстановленное уравнение квадратное приведенное будет вид иметь: x2-12 = -1*x. Можно подставить в него значение корней и убедиться, что равенство выполняется.
Обратное применение Виета теоремы, то есть вычисление корней по известному виду уравнения, позволяет для небольших целых чисел a, b и c быстро (интуитивно) находить решения.



























