Некоторые задачи в математике требуют умения вычислять значение корня квадратного. К таким задачам относится решение уравнений второго порядка. В данной статье приведем эффективный метод вычисления квадратных корней и используем его при работе с формулами корней квадратного уравнения.
Что такое квадратный корень?
В математике этому понятию соответствует символ √. Исторические данные говорят, что он начал использоваться впервые приблизительно в первой половине XVI века в Германии (первый немецкий труд по алгебре Кристофа Рудольфа). Ученые полагают, что указанный символ является трансформированной латинской буквой r (radix означает "корень" на латыни).

Корень из какого-либо числа равен такому значению, квадрат которого соответствует подкоренному выражению. На языке математики это определение будет выглядеть так: √x = y, если y2 = x.
Корень из положительного числа (x > 0) является также числом положительным (y > 0), однако если берут корень из отрицательного числа (x < 0), то его результатом уже будет комплексное число, включающее мнимую единицу i.
Приведем два простых примера:
√9 = 3, поскольку 32 = 9; √(-9) = 3i, поскольку i2 = -1.
Итерационная формула Герона для нахождения значений корней квадратных
Приведенные выше примеры являются очень простыми, и вычисление корней в них не представляет никакого труда. Сложности начинают появляться уже при нахождении значений корня для любого значения, которое не может быть представлено в виде квадрата натурального числа, например √10, √11, √12, √13, не говоря уже о том, что на практике необходимо находить корни для нецелых чисел: например √(12,15), √(8,5) и так далее.
Во всех вышеназванных случаях следует применять специальный метод вычисления корня квадратного. В настоящее время таких методов известно несколько: например разложение в ряд Тейлора, деление столбиком и некоторые другие. Из всех известных методов, пожалуй, наиболее простым и эффективным является использование итерационной формулы Герона, которая также известна как вавилонский способ определения квадратных корней (существуют свидетельства, что древние вавилоняне применяли ее в своих практических вычислениях).
Пусть необходимо определить значение √x. Формула нахождения квадратного корня имеет следующий вид:
an+1 = 1/2(an+x/an), где limn->∞(an) => x.
Расшифруем эту математическую запись. Для вычисления √x следует взять некоторое число a0 (оно может быть произвольным, однако для быстрого получения результата следует выбирать его таким, чтобы (a0)2 было максимально близко к x. Затем подставить его в указанную формулу вычисления квадратного корня и получить новое число a1, которое уже будет ближе к искомому значению. После этого необходимо уже a1 подставить в выражение и получить a2. Эту процедуру следует повторять до получения необходимой точности.
Пример применения итерационной формулы Герона
Описанный выше алгоритм получения корня квадратного из некоторого заданного числа для многих может звучать достаточно сложно и запутанно, на деле же оказывается все гораздо проще, поскольку эта формула сходится очень быстро (особенно если выбрано удачное число a0).
Приведем простой пример: необходимо вычислить √11. Выберем a0 = 3, так как 32 = 9, что ближе к 11, чем 42 = 16. Подставляя в формулу, получим:
a1 = 1/2(3 + 11/3) = 3,333333;
a2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Дальше нет смысла продолжать вычисления, поскольку мы получили, что a2 и a3 начинают отличаться лишь в 5-м знаке после запятой. Таким образом, достаточно было применить всего 2 раза формулу, чтобы вычислить √11 с точностью до 0,0001.
В настоящее время широко используются калькуляторы и компьютеры для вычисления корней, тем не менее отмеченную формулу полезно запомнить, чтобы иметь возможность вручную вычислять их точное значение.
Уравнения второго порядка
Понимание того, что такое корень квадратный, и умение его вычислять используется при решении квадратных уравнений. Этими уравнениями называют равенства с одной неизвестной, общий вид которых приведен на рисунке ниже.
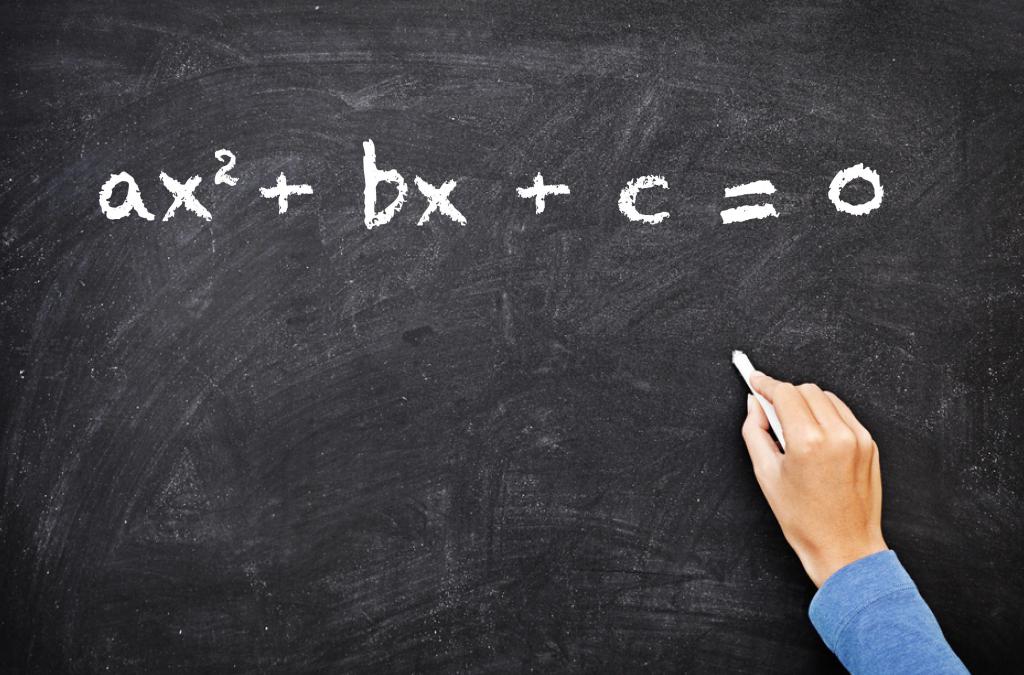
Здесь c, b и a представляют собой некоторые числа, причем a не должно равняться нулю, а значения c и b могут быть совершенно произвольными, в том числе и равными нулю.
Любые значения икса, удовлетворяющие указанному на рисунке равенству, называются его корнями (следует не путать это понятие с квадратным корнем √). Поскольку рассматриваемое уравнение имеет 2-й порядок (x2), то корней для него не может быть больше, чем два числа. Рассмотрим далее в статье, как находить эти корни.
Нахождения корней квадратного уравнения (формула)
Этот способ решения рассматриваемого типа равенств также называется универсальным, или методом через дискриминант. Его можно применять для любых квадратных уравнений. Формула дискриминанта и корней квадратного уравнения имеет следующий вид:
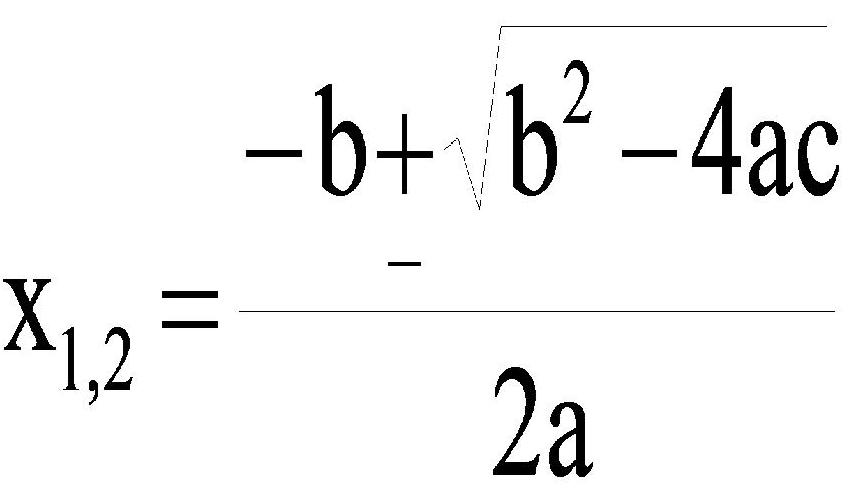
Из нее видно, что корни зависят от значения каждого из трех коэффициентов уравнения. Более того, вычисление x1 отличается от расчета x2 только знаком перед корнем квадратным. Подкоренное выражение, которое равно b2 - 4ac, является не чем иным, как дискриминантом рассматриваемого равенства. Дискриминант в формуле корней квадратного уравнения играет важную роль, поскольку он определяет число и тип решений. Так, если он равен нулю, то решение будет всего одно, если он положительный, то уравнение обладает двумя действительными корнями, наконец, отрицательный дискриминант приводит к двум комплексным корням x1 и x2.
Теорема Виета или некоторые свойства корней уравнений второго порядка
В конце XVI века один из основоположников современной алгебры француз Франсуа Виет, изучая уравнения второго порядка, смог получить свойства его корней. Математически их можно записать так:
x1 + x2 = -b / a и x1 * x2 = c / a.
Оба равенства легко может получить каждый, для этого необходимо лишь выполнить соответствующие математические операции с корнями, полученными через формулу с дискриминантом.

Совокупность этих двух выражений можно по праву назвать второй формулой корней квадратного уравнения, которая предоставляет возможность угадывать его решения, не используя при этом дискриминант. Здесь следует оговориться, что хотя оба выражения справедливы всегда, применять их для решения уравнения удобно только в том случае, если оно может быть разложено на множители.
Задача на закрепление полученных знаний
Решим математическую задачу, в которой продемонстрируем все приемы, обсуждаемые в статье. Условия задачи следующие: необходимо найти два числа, для которых произведение равно -13, а сумма составляет 4.

Это условие сразу напоминает о теореме Виета, применяя формулы суммы квадратных корней и их произведения, записываем:
x1 + x2 = -b / a = 4;
x1 * x2 = c / a = -13.
Если предположить, что a = 1, тогда b = -4 и c = -13. Эти коэффициенты позволяют составить уравнение второго порядка:
x2 - 4x - 13 = 0.
Воспользуемся формулой с дискриминантом, получим следующие корни:
x1,2 = (4 ± √D)/2, D = 16 - 4 * 1 * (-13) = 68.
То есть задача свелась к нахождению числа √68. Заметим, что 68 = 4 * 17, тогда, используя свойство квадратного корня, получим: √68 = 2√17.
Теперь воспользуемся рассмотренной формулой квадратного корня: a0 = 4, тогда:
a1 = 1/2(4 + 17/4) = 4,125;
a2 = 1/2(4,125 + 17/4,125) = 4,1231.
В вычислении a3 нет необходимости, поскольку найденные значения отличаются всего на 0,02. Таким образом, √68 = 8,246. Подставляя его в формулу для x1,2, получим:
x1 = (4 + 8,246)/2 = 6,123 и x2 = (4 - 8,246)/2 = -2,123.
Как видим, сумма найденных чисел действительно равна 4, если же найти их произведение, то оно будет равно -12,999, что удовлетворяет условию задачи с точностью до 0,001.



























