Физический смысл момента инерции: аналогия с линейным движением, примеры

Любая физическая величина, которая предлагается в математических уравнениях при изучении того или иного явления природы, несет некоторый смысл. Не является исключением из этого правила и момент инерции. Физический смысл этой величины подробно рассмотрен в данной статье.

Момент инерции: математическая формулировка

В первую очередь следует сказать, что рассматриваемая физическая величина используется для описания систем вращения, то есть таких движений объекта, которые характеризуются круговыми траекториями вокруг некоторой оси или точки.

Приведем математическую формулу момента инерции для материальной точки:

I = m*r².

Здесь m и r - масса и радиус вращения частицы (расстояние до оси) соответственно. Любое твердое тело, каким бы сложным оно ни было, мысленно можно разбить на материальные точки. Тогда формула момента инерции в общем виде будет иметь вид:

I = ∫_mr²dm.

Это выражение справедливо всегда, причем не только для трехмерных, но и для двумерных (одномерных) тел, то есть для плоскостей и стержней.

Из этих формул трудно понять смысл физический момента инерции, однако можно сделать важный вывод: он зависит от распределения массы в теле, которое вращается, а также от расстояния до оси вращения. Причем зависимость от r является более резкой, чем от m (см. знак квадрата в формулах).

Движение по окружности

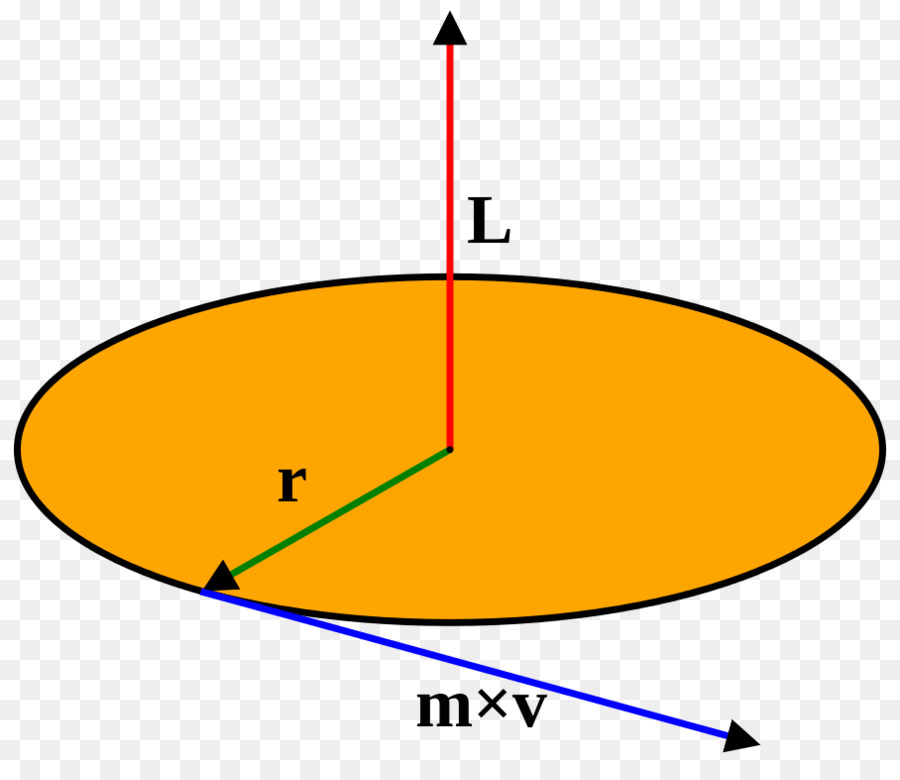
Понять, каков физический смысл момента инерции, невозможно, если не рассмотреть круговое движение тел. Не вдаваясь в подробности, приведем сразу два математических выражения, описывающих вращение:

I₁*ω₁ = I₂*ω₂;

M = I *dω/dt.

Верхнее уравнение носит название закона сохранения величины L (момента импульса). Оно означает, что какие бы изменения ни происходили внутри системы (сначала был момент инерции I₁, а затем он стал равным I₂), произведение I на угловую скорость ω, то есть момент импульса, будет оставаться неизменным.

Нижнее выражение демонстрирует изменение скорости вращения системы (dω/dt) при воздействии на нее некоторого момента силы M, который имеет внешний характер, то есть порождается силами, не связанными с внутренними процессами в рассматриваемой системе.

И в верхнем, и в нижнем равенствах присутствует I, причем чем больше ее значение, тем меньше будет угловая скорость ω или угловое ускорение dω/dt. В этом и заключается физический смысл момента инерции тела: он отражает способность системы сохранять свою угловую скорость. Чем больше I, тем сильнее проявляется эта способность.

Аналогия с линейным импульсом

Теперь перейдем к тому же выводу, что был озвучен в конце предыдущего пункта, проведя аналогию между вращательным и поступательным движениями в физике. Как известно, последнее описывается следующей формулой:

p = m*v.

Это простое выражение определяет импульс системы. Сравним его форму с таковой для момента импульса (см. верхнее выражение в предыдущем пункте). Мы видим, что величины v и ω имеют одинаковый смысл: первая характеризует скорость изменения линейных координат объекта, вторая - угловых координат. Поскольку обе формулы описывают процесс равномерного (равноуглового) движения, то величины m и I также должны иметь одинаковый смысл.

Теперь рассмотрим 2-й закон Ньютона, который выражается формулой:

F = m*a.

Обращая внимание на форму записи нижнего равенства в предыдущем пункте, имеем подобную рассмотренной ситуацию. Момент силы M в его линейной представлении - это сила F, а линейное ускорение a полностью аналогично угловому dω/dt. И снова мы приходим к эквивалентности массы и момента инерции.

Какой смысл несет масса в классической механике? Она является мерой инерции: чем больше m, тем труднее сдвинуть предмет с места, а тем более придать ему ускорение. То же самое можно сказать и о моменте инерции применительно к движению вращения.

Физический смысл момента инерции на бытовом примере

Зададимся простым вопросом о том, как легче крутить металлический стержень, например, арматуру - когда ось вращение направлена вдоль его длины или когда поперек? Конечно же, легче раскрутить стержень в первом случае, потому что его момент инерции для такого положения оси будет очень маленьким (для тонкого стержня он равен нулю). Поэтому достаточно зажать между ладошек предмет и легким движением привести его во вращение.

Кстати, описанный факт экспериментально проверили наши предки еще в стародавние времена, когда научились добывать огонь. Они раскручивали палочку с огромными угловыми ускорениями, что приводило к созданию больших сил трения и, как следствие, к выделению значительного количества теплоты.

Маховик авто - яркий пример использования большого значения момента инерции

В завершение хотелось бы привести, пожалуй, самый важный для современной техники пример использования физического смысла момента инерции. Маховик авто представляет собой сплошной стальной диск, имеющий относительно большие радиус и массу. Эти две величины обуславливают существование значительной величины I, характеризующей его. Маховик призван "смягчать" любые силовые воздействия на коленвал автомобиля. Импульсивный характер действующих моментов сил от цилиндров двигателя на коленвал сглаживается и делается плавным благодаря тяжелому маховику.

Кстати, чем больше момент импульса, тем больше энергии находится во вращающейся системе (аналогия с массой). Этот факт хотят использовать инженеры, запасая энергию торможения авто в маховике, чтобы впоследствии направить ее на разгон транспортного средства.