Понятие об угловом ускорении. Формулы кинематики и динамики вращения. Пример задачи

Вращение тел является одним из важных типов механического движения в технике и природе. В отличие от линейного перемещения, оно описывается собственным набором кинематических характеристик. Одной из них является угловое ускорение. Охарактеризуем эту величину в статье.

Движение вращения

Прежде чем говорить об угловом ускорении, опишем тип движения, к которому оно применяется. Речь идет о вращении, которое представляет собой перемещение тел по круговым траекториям. Чтобы вращение происходило, необходимо выполнение некоторых условий:

• наличие оси или точки вращения;
• наличие центростремительной силы, которая бы удерживала на круговой орбите тело.

Примерами этого типа движения являются различные аттракционы, например карусель. В технике вращение проявляет себя при движении колес и валов. В природе самым ярким примером этого типа движения является вращение планет вокруг собственной оси и вокруг Солнца. Роль центростремительной силы в названных примерах играют силы межатомного взаимодействия в твердых телах и гравитационное взаимодействие.

Кинематические характеристики вращения

К этим характеристикам относятся три величины: угловое ускорение, угловая скорость и угол поворота. Будем обозначать их греческими символами α, ω и θ соответственно.

Так как тело движется по окружности, то удобно рассчитывать угол θ, на который оно повернется за определенное время. Этот угол выражается в радианах (реже в градусах). Поскольку окружность имеет 2 × pi радиан, то можно записать равенство, связывающее θ с длиной дуги L поворота:

L = θ × r

Где r - радиус вращения. Эту формулу несложно получить, если вспомнить соответствующее выражение для длины окружности.

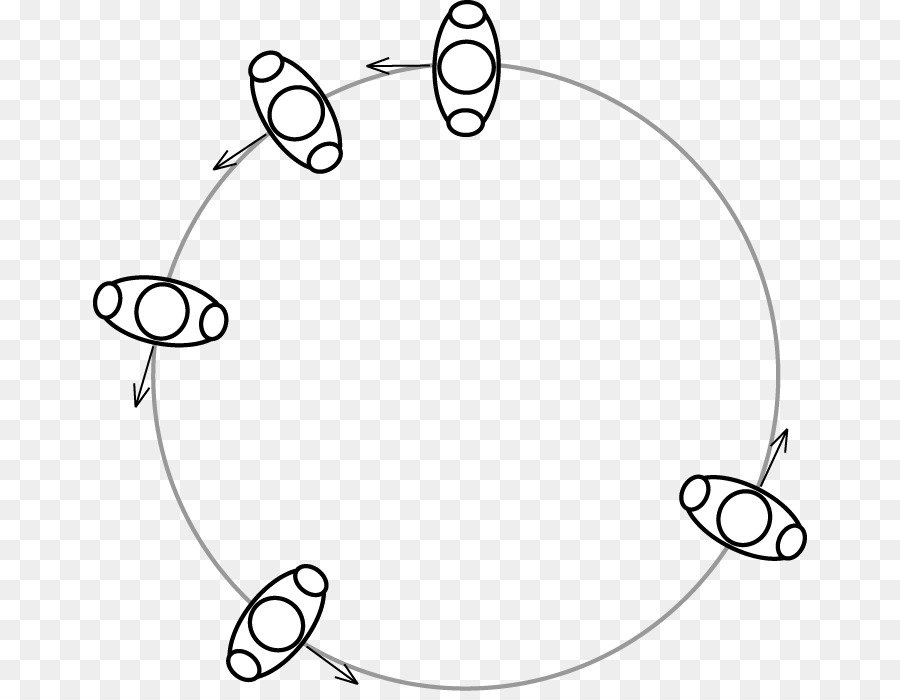
Угловая скорость ω, как и ее линейный аналог, описывает быстроту поворота вокруг оси, то есть она определяется согласно следующему выражению:

ω¯ = d θ / d t

Величина ω¯ является векторной. Направлена она вдоль оси вращения. Единицей ее измерения является радиан в секунду (рад/с).

Наконец, угловое ускорение - это физическая характеристика, которая определяет быстроту изменения величины ω¯, что математически записывается так:

α¯ = d ω¯/ d t

Вектор α¯ направлен в сторону изменения вектора скорости ω¯. Далее будет сказано, что угловое ускорение направлено в сторону вектора момента силы. Измеряют эту величину в радианах в квадратную секунду (рад/с²).

Момент силы и ускорение

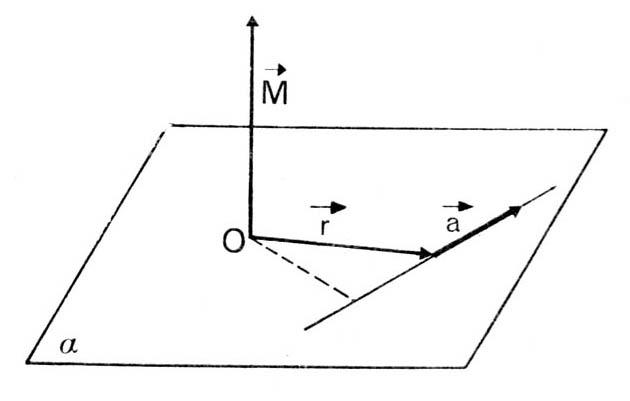
Если вспомнить закон Ньютона, который связывает в единое равенство силу и линейное ускорение, то, перенеся этот закон на случай вращения, можно записать следующее выражение:

M¯ = I × α¯

Здесь M¯ - момент силы, представляющий собой произведение силы, которая стремится раскрутить систему, на рычаг - расстояние от точки приложения силы до оси. Величина I является аналогом массы тела и называется моментом инерции. Записанная формула называется уравнением моментов. Из него угловое ускорение можно вычислить так:

α¯ = M¯/ I

Поскольку I - это скаляр, то α¯ всегда направлено в сторону действующего момента силы M¯. Направление M¯ определяется по правилу правой руки или правилу буравчика. Вектора M¯ и α¯ перпендикулярны плоскости вращения. Чем больший момент инерции имеет тело, тем меньшее значение углового ускорения способен сообщить системе фиксированный момент M¯.

Кинематические уравнения

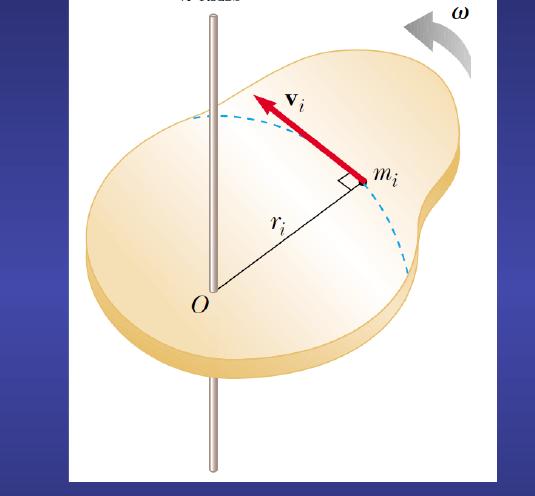
Чтобы понять, какую важную роль играет угловое ускорение для описания движения вращения, запишем формулы, связывающие изученные выше кинематические величины.

В случае равноускоренного вращения справедливы следующие математические соотношения:

ω = α × t;

θ = α × t² / 2

Первая формула показывает, что угловая скорость будет расти во времени по линейному закону. Второе выражение позволяет рассчитать угол, на который повернется тело за известное время t. Графиком функции θ(t) является парабола. В обоих случаях угловое ускорение - это постоянная величина.

Если воспользоваться приведенной в начале статьи формулой связи между L и θ, то можно получить выражение для α через линейное ускорение a:

α = a / r

Если α является постоянным, то при возрастании расстояния от оси вращения r будет пропорциональным образом увеличиваться линейное ускорение a. Именно поэтому для вращения пользуются угловыми характеристиками, в отличие от линейных, они не изменяются с увеличением или уменьшением r.

Пример задачи

Металлический вал, вращаясь с частотой 2 000 оборотов в секунду, начал замедлять свое движение и через 1 минуту полностью остановился. Необходимо рассчитать, с каким угловым ускорением происходил процесс торможения вала. Также следует вычислить количество оборотов, которые вал сделал до того, как остановиться.

Процесс замедления вращения описывается таким выражением:

ω = ω₀ - α × t

Начальная угловая скорость ω₀ определяется через частоту вращения f таким образом:

ω₀ = 2 × pi × f

Поскольку время торможения нам известно, тогда получаем значение ускорения α:

α = ω₀ / t = 2 × pi × f / t = 209,33 рад/с²

Это число следует взять со знаком минус, поскольку речь идет о торможении системы, а не об ее ускорении.

Для определения числа оборотов, которые вал сделает во время торможения, применим выражение:

θ = ω₀ × t - α × t² / 2 = 376 806 рад.

Полученное значение угла поворота θ в радианах просто переводится в число сделанных оборотов валом до его полной остановки с помощью простого деления на 2 × pi:

n = θ / (2 × pi) = 60 001 оборот.

Таким образом, мы получили все ответы на вопросы задачи: α = -209,33 рад/с², n = 60 001 оборот.