Среди главных характеристик карт местности чаще всех выделяют данную. Это точность масштаба. В статье мы разберем, что скрывает в себе данное понятие. Также рассмотрим, что такое масштаб вообще, охарактеризуем его основные разновидности. Разберем, как понятие "графическая точность" связано с предметом нашего разговора.
Что это?
Масштаб - это важное уточнение, показывающее, во сколько каждая линия, что была нанесена на чертеж, план, меньше или больше настоящих размеров объекта, который она изображает. Такие уточнения представляются на чертежных документах и картах как численно, так и графически.
Масштабы планов, точность масштабов - понятия, которые можно встретить в самых разнообразных сферах:
- Картография.
- Проектирование.
- Геодезия.
- Фотография.
- Моделизм.
- Программирование.
- Математика.
- Кинотехника.
Некоторые из этих применений, их особенности мы рассмотрим по ходу статьи.
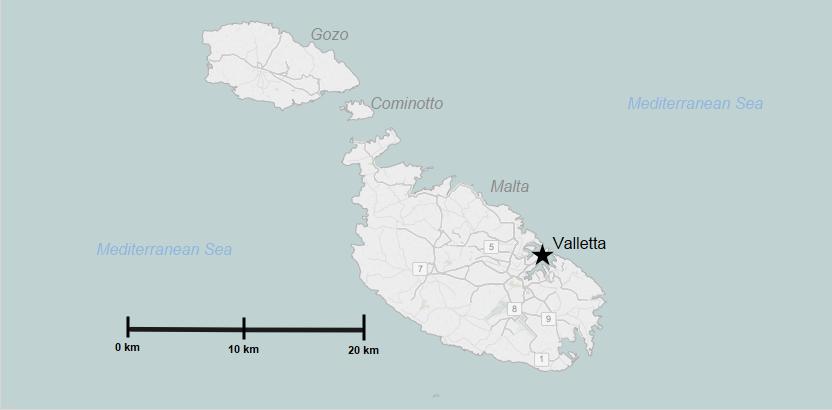
Точность масштаба
И теперь определение ключевого понятия. Точность масштаба - часть горизонтального проложения линии, которая будет означать 0,1 мм на чертеже. Почему выбрано такое значение?
0,1 мм тут принят из-за того, что это наименьший отрезок, который может различить глаз человека на изображении без использования специальной техники, инструментов, приборов.
Приведем конкретный пример. Дано 1:10000. Точность масштаба станет составлять, соответственно, 1 м. Разберем подробнее:
- 1 см на плане или изображении - это 10 000 см (или 100 м) на реальной местности.
- 1 мм на изображении - это 1 000 см (или 10 м).
- 0,1 мм - это 100 см (или 1 м) на реальной местности.
Таким образом несложно определить предельную точность масштаба. Это расстояние реальной поверхности, равное 0,1 мм на карте - минимальному отрезку, который способен различить человек.
Графическая точность
А теперь познакомимся с графической точностью масштабов. Это еще одна значимая характеристика при использовании планов и карт.
Графическая точность связывается с разрешением "и" глаза человека. В свою очередь, оно составляет "Г". Отсюда Г=и.
То есть, если угол "и" между векторами на две точки "В" и "Л" при рассматривании их наблюдателем с нормальным уровнем зрения составляет "Г" или же более, то они будут восприниматься, как две точки. Если же данный угол к понятию разрешения меньше "Г", то "Л" и "В" будут восприниматься человеком как одна точка.
Лучше всего тут познакомиться с определением точности масштаба на конкретном примере. Допустим, человек рассматривает карту с наилучшего расстояния "б", равного 35 см. Значение Г=и. Теперь нужно определить наименьшее расстояние (то есть, графическую точность) между "В" и "Л", при котором они еще будут восприниматься наблюдателем в виде двух разных точек. Тут проводится такое вычисление:
1 - ис! - 1/3438 х 350 мм = 0,1 мм.
1/3438 - это значение угла и=Г, которое в данном случае выражено в радианах (3438' - количество минут в радиане).
Таким образом, вышедшее значение 0,1 мм - графическая точность плана или карты.
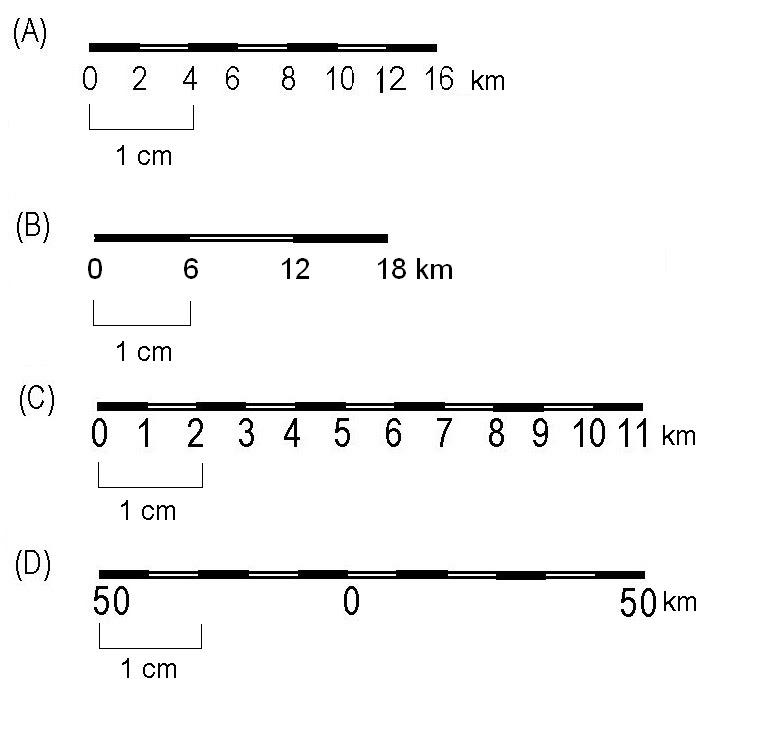
Связь понятий
А теперь посмотрим, как вышеобозначенный термин соотносится с главным. Точность масштаба - это, как мы помним, расстояние на поверхности Земли, что равняется 0,1 мм на документе.
Можно вывести формулу:
Т = гМ = 0,1 М мм.
Расшифруем ее элементы:
- Т - точность масштаба.
- М - знаменатель масштаба.
- г = 0,1 мм - графическая точность.
Отсюда можно вывести и связанную трактовку. Точность масштаба - графическая точность, что выражается в масштабе карты или плана. И что же в итоге? Графическая точность станет выступать константой (0,1 мм) для всех существующих масштабов.
Соответственно, точность масштаба станет изменяться вместе с ним самим. Она будет тем выше, чем крупнее составитель выбрал масштаб.
А теперь разберемся с особенностями такой характеристики, как масштаб, в различных сферах применения.
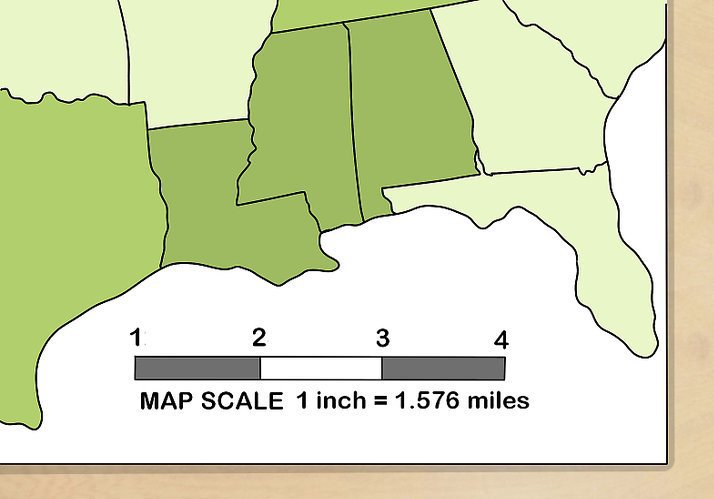
Проектирование, геодезия и картография
Мы в курсе, что обозначает точность "500" масштаба - 1:500. Рассмотрим теперь, какие его разновидности характерны для сферы проектирования, картографии и геодезии:
- Численный масштаб. Показатель прописывается в виде дроби. В ее числителе будет стоять единица, а в знаменателе - какая-либо степень уменьшения проекции на карте. Для примера возьмем масштаб 1:5 000. Он обозначает, что 1 см на плане, карте - это 5 000 см (или 50 м) на реальной местности. Соответственно, тут будет более крупным тот масштаб, который отличается меньшим знаменателем. Так, 1:1 000 будет крупнее, нежели 1:20 000.
- Именованный масштаб. Составитель карты прописывает на документе, какое расстояние на реальной местности равняется 1 см на плане. Вот пример: "В 1 сантиметре - 1000 километров". Или же кратко: "1 см = 100 км".
- Графический масштаб. В свою очередь, будет разделяться на поперечный и линейный. Разберем их отдельно.

Разновидности графической категории
Какова же точность масштаба - поперечного масштаба? Познакомимся с характеристиками:
- Линейный. Такой графический масштаб на карте представляется в виде линейки, которая будет разделена на реальные части.
- Поперечный. Это графический масштаб, представленный в виде номограммы. Ее построение зиждется на пропорциональности частей параллельных прямых, что пересекают стороны угла. Такой масштаб применим для более точного измерения протяженности линий на планах. Пользуются им таким образом: производят на нижней линии данного поперечного масштаба замер длины так, чтобы правый конец находился на целом расстоянии (ОМ), а левый был за 0. Если при этом левая ножка окажется между десятыми делениями, соответственно, левого отрезка (от 0), то специалист подымает обе ножки измерителя кверху. Пока левая ножка измерителя не встанет уже на пересечении какой-либо горизонтальной линии и какой-либо трансверсали. А вот правая ножка тоже должна быть на этой горизонтальной черте. Минимальная ЦД здесь - 0,2 мм. Соответственно, наименьшая точность - 0,1 мм.
Ряд масштабов изображений в проектировании
Мы уже знаем, что означает точность масштаба 1:500. Но в каких случаях ее выбирает составитель? Разберем и этот вопрос:
- Масштабы уменьшения. Соответственно, используются в случаях, когда на плане нужно изобразить объект, местность, значительно превышающую его по площади. Если же составитель обращается к проектированию генеральных планов особо крупных размеров, то он ему пригодится использование следующих масштабов: 1:2 000, 1:5 000, 1:10 000, 1:20 000, 1:25 000, 1:50 000.
- Натуральная величина. Если требуется изобразить объект на плане так, "как он есть", то обращаются к масштабу "один к одному". Соответственно 1 см реальной длины тут будет соответствовать 1 см длины на плане.
- Масштабы увеличения. Необходимы в случаях, когда требуется изобразить на плане слишком маленький объект для детального ознакомления с его внешним видом, устройством.
В фотографии
Конечно, точность масштаба 1:10 000 более связывается с картографией. Но это применимо и для мира фотосъемки. Под масштабом здесь подразумевается отношение так называемых линейных размеров изображения, полученного на сверхчувствительной матрице или же на фотопленке, к размеру проекции соответствующей зоны проекции на плоскость, которая перпендикулярна к камере.
Есть фотографы, которые измеряют масштаб в виде отношения размеров реального объекта к его размерам на экране, фотобумаге или другом носителе. Но верный способ определения масштаба в фотографии зависит только от контекста, в котором использовано изображение.
В фотосъемке масштаб характеризуется важным значением и при расчете глубины какого-либо резко изображаемого объекта, пространства. Сегодня специалистам доступен весьма широкий выбор диапазонов масштабов от бесконечно малого (применяется при съемке далеких небесных тел) до весьма крупного (без использования специальных оптических насадок, например, сегодня возможно получить снимок масштабом 10:1).
Здесь макрофотографией считается уже съемка в масштабе 1:1 (и, соответственно, крупнее). Но с распространением цифровых компактных фотоаппаратов макросъемкой также стали называть стиль, когда объектив располагают слишком близко к объекту. Если рассматривать классическое определение, то подобное толкование не будет верным.

В моделизме
Для каждого из видов стендового (или масштабного) моделизма определены свои масштабные ряды. Они состоят из нескольких масштабов, характеризующихся определенной степенью уменьшения. Что интересно, для каждого из видов моделизма (железнодорожного, автомобильного, судомоделизма, военной техники, авиамоделизма) есть определенные исторически сформированные масштабные ряды, которые не пересекаются с иными.
Здесь масштаб исчисляется по простой формуле:
L / М = Х.
Расшифруем:
- L - параметры оригинала.
- М - необходимый для работы масштаб.
- Х - нужное значение.
В программировании
В этой сфере будет важен так называемый масштаб времени. Разберемся, что это.
В ОС с разделением времени весьма важную роль имеет предоставление конкретно взятым задачам "режима реального времени". Он отличается тем, что обработка внешних событий идет без дополнительных задержек или пропусков. Здесь важным будет еще одно понятие - "реальный масштаб времени". Но стоит понимать, что к масштабу на картах он прямого отношения не имеет. Это всего лишь терминологическая условность.
В кинотехнике
В кинотехнике тоже важна точность масштаба времени. Под последним подразумевается количественный показатель замедления либо ускорения движения, который будет равняться отношению проекционный частоты кадров к частоте съемочной.
Рассмотрим это на простом примере. Проекционная частота кадров при съемке фильма составляет 24 кадра/сек. Киносъемка производилась при этом "со скоростью" 72 кадра/сек. Масштаб времени в данном случае будет равен 1:3.
А что тогда будет означать, к примеру, 2:1? Это ускоренное в два раза по сравнению со стандартным протеканием происходящего на экране.
В математике
В этой сфере под масштабом понимается линейное соотношение двух размеров. Также во многих практически применимых областях так будет называться отношение размера изображения к реальному размеру изображаемого.
В математике масштаб - это отношение какого-либо расстояния на карте уже к реальному расстоянию на реальной местности. Если рассмотреть на примере, это то же самое, что и в картографии. Допустим, 1:100 000 000. Значит, 1 см на изображении - это 100 000 см в реальности. То есть, тысяча метров или один километр.
Масштаб - широко применимая характеристика. Это стандартная и неотъемлемая составляющая при разработке планов, чертежей объектов, карт местности. Используется при проектировании, в геодезии, картографии, актуальна при фотосъемке, в кинотехнике, программировании и математике. Саму же ее главным образом характеризует точность - отношение реального расстояния к принятому на карте.


























