В математике существует понятие "множество", так же как и существуют примеры сопоставления этих самых множеств между собой. Названиями видов сопоставления множеств выступают следующие слова: биекция, инъекция, сюръекция. Ниже о каждом из них рассказано подробнее.
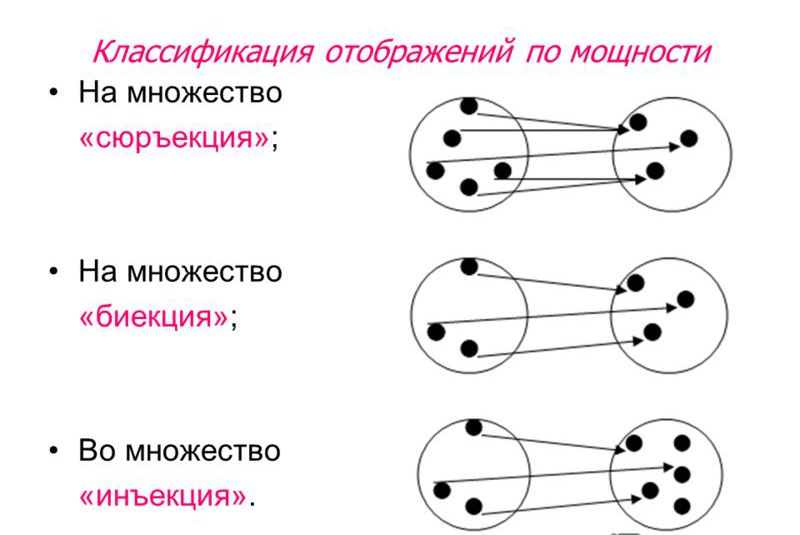
Биекция - это... это что?
Одна группа элементов первого множества сопоставляется со второй группой элементов из второго множества в таком виде: каждый один элемент первой группы напрямую сопоставляется с другим одним элементом из второй группы, и при этом не возникает ситуации с нехваткой или перебором элементов какой-либо из двух групп множеств.
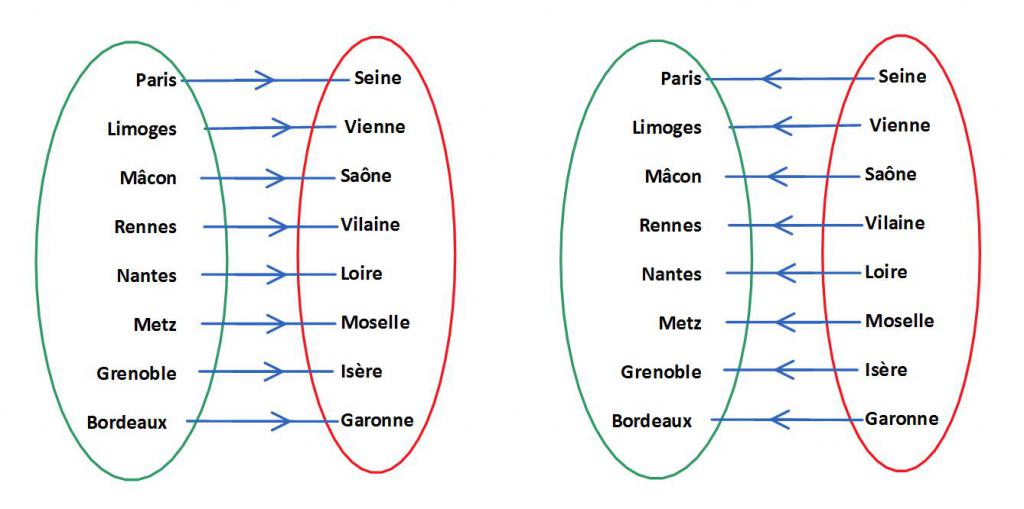
Формулировка основных свойств:
- Один элемент к одному.
- Не остается лишних элементов при сопоставлении и сохраняется первое свойство.
- Возможно обратное отображение сопоставления с сохранением общего вида.
- Биекция - это такая функция, что является одновременно инъективной и сюръективной.
Биекция с научной стороны
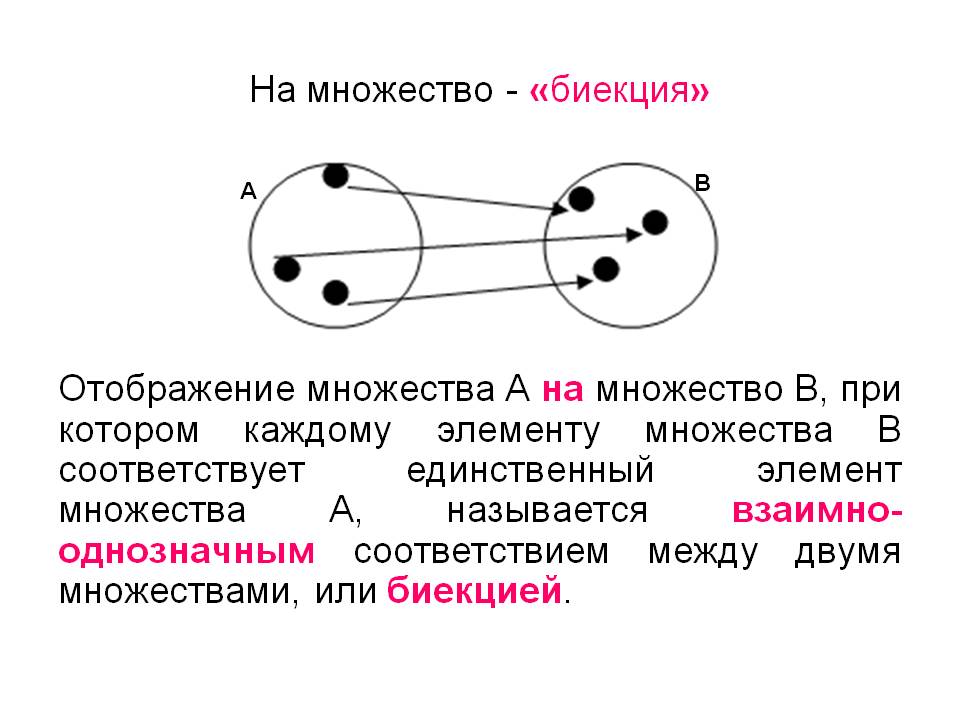
Биективные функции - именно изоморфизмы в категории "набор и набор функций". Однако биекции не всегда изоморфизмы для более сложных категорий. Например, в определенной категории групп морфизмы должны быть гомоморфизмами, поскольку они должны сохранять структуру группы. Поэтому изоморфизмы являются групповыми, которые являются биективными гомоморфизмами.
Понятие "взаимно-однозначное соответствие" обобщается на частичные функции, где их называют частичными биекциями, хотя частичная биекция – это то, что должно быть инъекцией. Причина этой релаксации заключается в том, что частичная (правильная) функция уже не определена для части своей области. Таким образом, нет веских оснований ограничивать ее обратную функцию полной, т. е. определенной повсюду в ее области. Множество всех частичных биекций на данный базовый набор называется симметрической инверсной полугруппой.
Другой способ определения одного и того же понятия: стоит сказать, что частичная биекция множеств из A в B - это любое отношение R (частичная функция) с тем свойством, что R - это графа биекции f:А'→B', где А' является подмножеством A, и B' является подмножеством В.
Когда частичная биекция находится на одном и том же множестве, ее иногда называют частичным преобразованием "один к одному". Примером является преобразование Мебиуса, просто определенное на комплексной плоскости, а не его завершение в расширенную комплексную плоскость.
Инъекция
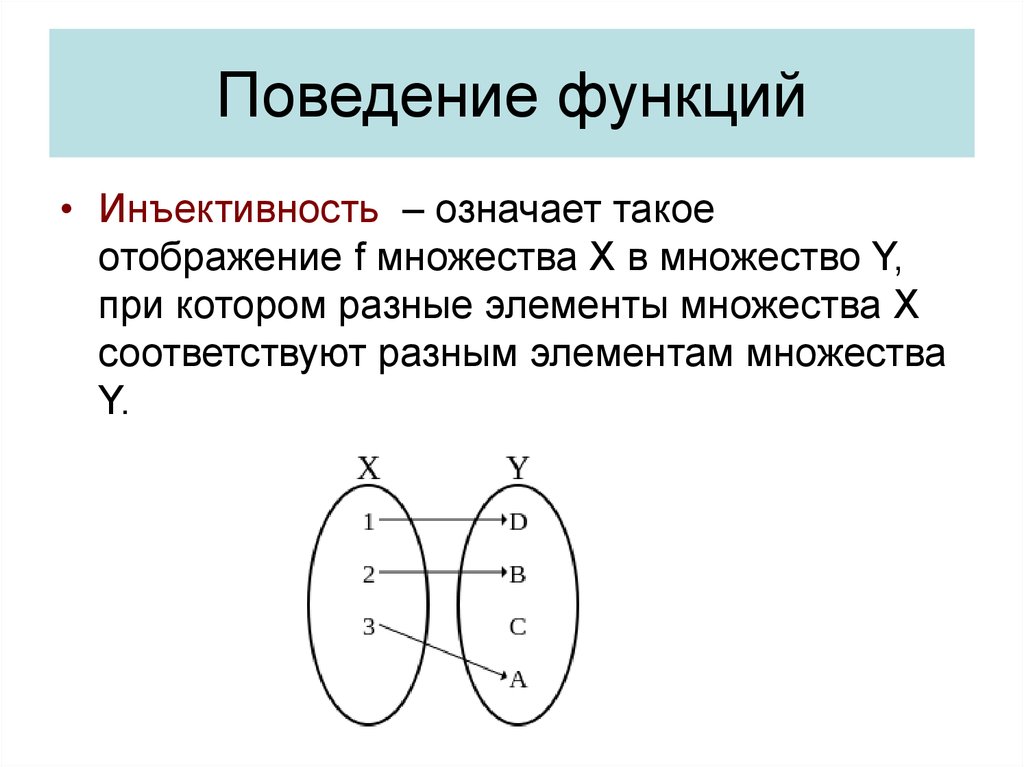
Одна группа элементов первого множества сопоставляется со второй группой элементов из второго множества в таком виде: каждый один элемент первой группы сопоставляется с другим одним элементом второй, но не все из них преобразуются в пары. Количество неспаренных элементов зависит от разности числа этих самых элементов в каждом из множеств: если одно множество состоит из тридцати одного элемента, а в другом на семь больше, то количество неспаренных элементов - семь. Направлена инъекция во множество. Биекция и инъекция схожи между собой, но не более чем просто схожи.
Сюръекция
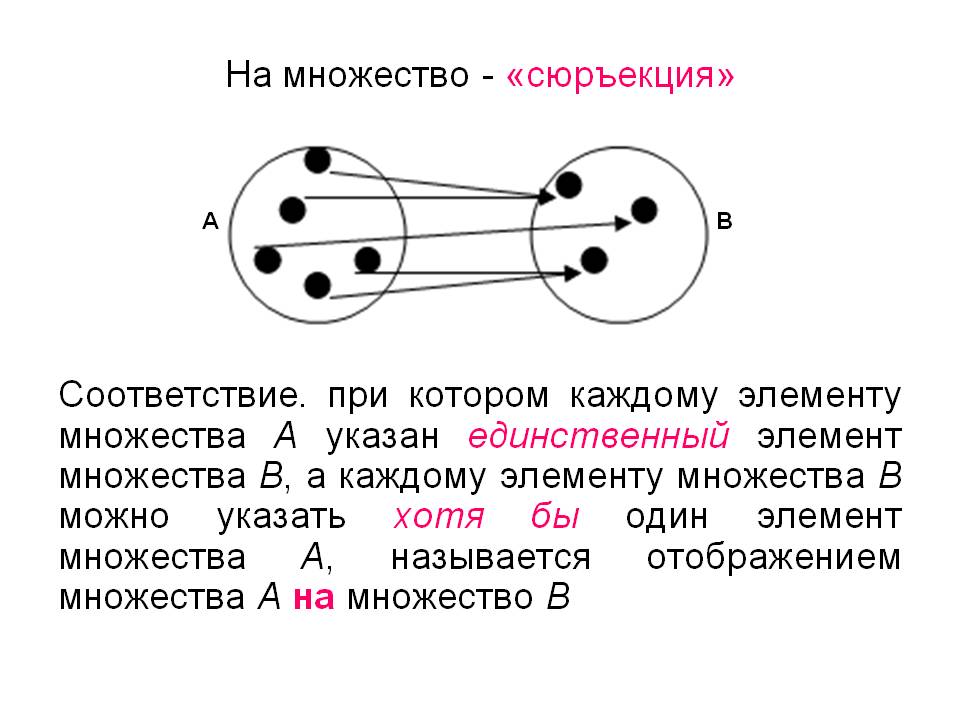
Одна группа элементов первого множества сопоставляется со второй группой элементов из второго множества в таком виде: каждый элемент какой-либо группы образует пару, даже при условии существования разницы между количеством элементов. Из этого следует, что один элемент из одной группы может создать пару с несколькими элементами из другой группы.
Ни биективная, ни инъективная, ни сюръективная функция
Это функция биективного и сюръективного вида, но с остаточным элементом (неспаренным) => инъекция. В такой функции явно присутствует связь между биекцией и сюръекцией, так как она непосредственно включает в себя данные два вида сопоставления множеств. Так вот, совокупность всех видов данных функций не является ни одним из них в отдельности.
Объяснение всех видов функций
Например, наблюдатель увлечен следующим. Проходят соревнования по стрельбе из лука. Каждый из участников желает попасть в мишень (в целях облегчения задачи: то, куда именно попадает стрела, не учитывается). Всего трое участников и три мишени - это первая площадка (участок) для проведения турнира. На последующих участках сохраняется количество лучников, но изменяется число мишеней: на втором - четыре мишени, на следующем - тоже четыре, а на четвертом - пять. Каждый участник стреляет по каждой мишени.
- Первая площадка для проведения турнира. Первый лучник попадает только в одну мишень. Второй попадает только в одну мишень. Третий повторяет за другими, и все лучники попали в разные мишени: те, которые располагаются напротив них. В итоге 1 (первый лучник) попал в мишень (а), 2 - в (б), 3 - в (в). Наблюдается следующая зависимость: 1 – (а), 2 – (б), 3 – (в). Выводом будет являться суждение о том, что такое сопоставление множеств - это биекция.
- Вторая площадка для проведения турнира. Первый лучник попадает только в одну мишень. Второй также попадает только в одну мишень. Третий особо не старается и повторяет все за другими, но условие то же - все лучники попали в разные мишени. Но, как было сказано ранее, на второй площадке уже четыре мишени. Зависимость: 1 - (а), 2 - (б), 3 - (в), (г) - неспаренный элемент множества. В этом случае выводом будет являться суждение о том, что такое сопоставление множеств - это инъекция.
- Третья площадка для проведения турнира. Первый лучник попадает только в одну мишень. Второй снова попадает только в одну мишень. Третий решает взять себя в руки и поражает третью и четвертую мишени. В итоге зависимость: 1 - (а), 2 - (б), 3 - (в), 3 - (г). Здесь же выводом будет являться суждение о том, что такое сопоставление множеств - это сюръекция.
- Четвертая площадка для проведения турнира. С первым все уже ясно, он поражает только одну мишень, в которой скоро не останется места для уже надоевших попаданий. Теперь второй берет на себя роль еще недавнего третьего и снова попадает только в одну мишень, повторяя за первым. Третий продолжает держать себя в руках и не перестает знакомить свою стрелу с третьей и четвертой мишенью. Пятая, правда, ему все же оказалась неподвластна. Так, зависимость: 1 - (а), 2 - (б), 3 - (в), 3 - (г), (д) - неспаренный элемент множества мишеней. Вывод: такое сопоставление множеств - это не сюръекция, не инъекция и не биекция.
Теперь построить биекцию, инъекцию или сюръекцию не станет проблемой, так же как и найти отличия между ними.



























