Что такое сила трения качения и по какой формуле ее можно вычислить?

Современное состояние техники выглядело бы совершенно иначе, если бы человечество в далеком прошлом не научилось использовать для своих благ силу трения качения. Что она собой представляет, почему появляется и как ее можно рассчитать, эти вопросы рассматриваются в статье.

Что это трение качения?

Под ним понимают физическую силу, которая появляется во всех случаях, когда один предмет не скользит, а катится по поверхности другого. Примерами силы трения качения являются движение деревянного колеса телеги по грунтовой дороге или перемещение колеса автомобиля по асфальту, качение металлических шариковых и игольчатых подшипников по стальной оси, перемещение малярного валика по стене и так далее.

В отличие от сил трения покоя и скольжения, причиной которых являются взаимодействия на атомном уровне шероховатых поверхностей тела и поверхности, причина появления трения в результате качения заключается в гистерезисе деформации.

Объясним названный факт на примере колеса. Когда оно контактирует с абсолютно любой твердой поверхностью, то в зоне контакта происходит его микродеформация в упругой области. Как только колесо повернется на некоторый угол, то эта упругая деформация исчезнет, и тело восстановит свою форму. Тем не менее в результате качения колеса происходит повторение циклов сжатия и восстановления формы, которые сопровождаются потерей энергии и микроскопическими нарушениями в структуре поверхностных слоев колеса. Эти потери называются гистерезисом. Они при движении проявляются в возникновении силы трения качения.

Качение недеформируемых тел

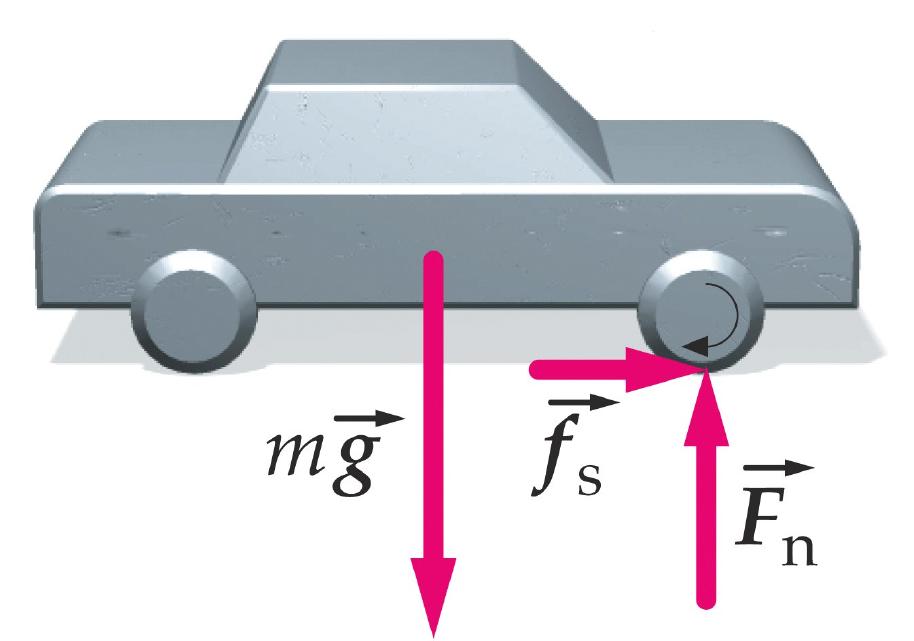
Рассмотрим идеальный случай, когда колесо, двигаясь по абсолютно твердой поверхности, не испытывает микродеформаций. В этом случае зона его контакта с поверхностью будет соответствовать прямому отрезку, площадь которого равна нулю.

При движении на колесо действуют четыре силы. Это сила тяги F, сила реакции опоры N, вес колеса P и трение f_r. Первые три силы носят центральный характер (действуют на центр масс колеса), поэтому крутящего момента они не создают. Сила f_r действует по касательной к ободу колеса. Момент трения качения равен:

M = f_r*r.

Здесь радиус колеса обозначен буквой r.

Силы N и P действуют по вертикали, поэтому в случае равномерного движения сила трения f_r будет равна силе тяги F:

F = f_r.

Любая бесконечно маленькая сила F будет способна преодолеть величину f_r, и колесо начнет движение. Этот вывод приводит к тому, что в случае недеформируемого колеса сила трения качения равна нулю.

Качение деформируемых (реальных) тел

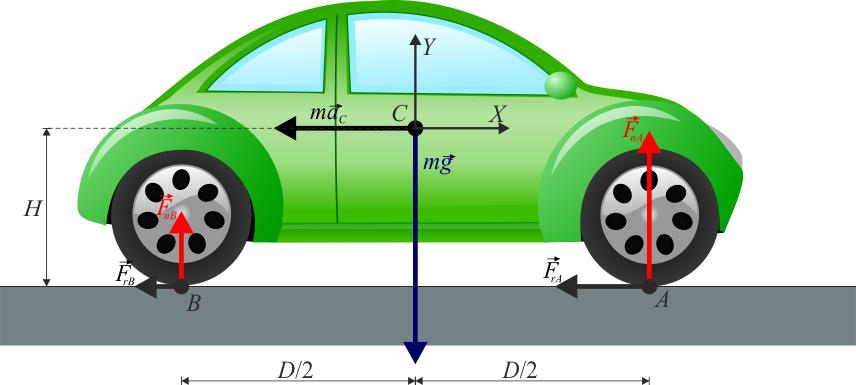
В случае реальных тел в результате деформации колеса его площадь опоры на поверхность не равна нулю. В первом приближении она представляет собой прямоугольник, со сторонами l и 2*d. Где l - ширина колеса, которая нас сильно не интересует. Появление же силы трения качения обязано именно значению 2*d.

Как и в случае с недеформируемым колесом, на реальный объект также действуют четыре названные выше силы. Все соотношения между ними сохраняются за исключением одного: сила реакции опоры в результате деформации будет действовать не через ось на колесо, а будет смещена относительно нее на расстояние d, то есть она будет принимать участие в создании крутящего момента. Формула для момента M в случае реального колеса принимает вид:

M = N*d - f_r*r.

Равенство нулю величины M является условием равномерного качения колеса. В результате приходим к равенству:

f_r = d/r*N.

Поскольку N равно весу тела, получаем конечную формулу для силы трения качения:

f_r = d/r*P.

Это выражение содержит полезный результат: с увеличением радиуса r колеса уменьшается сила трения f_r.

Коэффициент сопротивления качению и коэффициент качения

В отличие от сил трения покоя и скольжения, качение характеризуется двумя зависимыми друг от друга коэффициентами. Первый из них - это величина d, описанная выше. Она называется коэффициентом сопротивления качению, поскольку чем больше ее значение, тем больше сила f_r. Для колес поездов, автомобилей, металлических подшипников значение d лежит в пределах десятых долей миллиметра.

Второй коэффициент - это собственно качения коэффициент. Он является безразмерной величиной и равен:

C_r = d/r.

Во многих таблицах приводят именно эту величину, поскольку его удобнее применять для решения практических задач, чем значение d. В большинстве практических случаев величина C_r не превышает нескольких сотых (0,01- 0,06).

Условие качения реальных тел

Выше мы получили формулу для силы f_r. Запишем ее через коэффициент C_r:

f_r = C_r*P.

Видно, что ее форма аналогична таковой для силы трения покоя, в которой вместо C_r используется величина µ - коэффициент трения покоя.

Сила тяги F приведет к качению колеса только в том случае, если она будет больше f_r. Однако, тяга F может привести и к скольжению, если она превысит соответствующую силу покоя. Таким образом, условие качения реальных тел заключается в том, чтобы сила f_r была меньше силы трения покоя.

В большинстве случаев значения коэффициента µ на 1-2 порядка превышают величину C_r. Тем не менее, в некоторых ситуациях (наличие на поверхности качения снега, льда, маслянистых жидкостей, грязи) µ может становиться меньше C_r. В последнем случае будет наблюдаться проскальзывание колеса.