Трение - физическое явление, с которым человек борется с целью его уменьшения в любых вращающихся и скользящих частях механизмов, без которого, однако, невозможно движение ни одного из этих механизмов. В данной статье рассмотрим с точки зрения физики, что такое сила трения качения.
Какие виды сил трения существуют в природе?

В первую очередь рассмотрим, какое место трение качения занимает среди других сил трения. Эти силы возникают в результате контакта двух разных тел. Это могут быть тела твердые, жидкие или газообразные. Например, полет самолета в тропосфере сопровождается наличием трения между его корпусом и молекулами воздуха.
Рассматривая исключительно твердые тела, выделяют силы трения покоя, скольжения и качения. Каждый из нас замечал: чтобы сдвинуть с места коробок, находящийся на полу, необходимо вдоль поверхности пола приложить некоторую силу. Значение силы, которое выведет коробок из состояния покоя, будет по модулю равно силе трения покоя. Последняя действует между дном коробка и поверхностью пола.
Как только коробок начал свое движение, необходимо прилагать постоянную силу, чтобы сохранять это движение равномерным. Связан этот факт с тем, что между контактом пола и коробком на последний действует сила трения скольжения. Как правило, она на несколько десятков процентов меньше, чем трение покоя.
Если под коробок положить круглые цилиндры из твердого материала, то перемещать его станет гораздо легче. На вращающиеся в процессе движения цилиндры под коробком будет действовать сила трения качения. Она обычно намного меньше предыдущих двух сил. Именно поэтому изобретение человечеством колеса стало огромным скачком в сторону прогресса, ведь люди получили возможность перемещать гораздо большие грузы с помощью небольшой приложенной силы.
Физическая природа трения качения
Почему возникает сила трения качения? Этот вопрос является непростым. Для ответа на него следует детально рассмотреть, что происходит с колесом и поверхностью в процессе качения. В первую очередь они не являются идеально гладкими - ни поверхность колеса, ни поверхность, по которой оно катится. Тем не менее это не основная причина появления трения. Главной же причиной является деформация одного или обоих тел.
Любые тела, из какого бы твердого материала они ни состояли, деформируются. Чем больше вес тела, тем большее давление оно оказывает на поверхность, а значит, деформируется само в точке контакта и деформирует поверхность. Эта деформация в ряде случаев настолько мала, что не превышает предела упругости.
В процессе качения колеса деформированные участки после прекращения контакта с поверхностью восстанавливают исходную форму. Тем не менее эти деформации циклически повторяются с новым оборотом колеса. Любая циклическая деформация, даже если она лежит в пределе упругости, сопровождается гистерезисом. Иными словами, на микроскопическом уровне форма тела до и после деформации отличается. Гистерезис циклов деформации в процессе качения колеса приводит к "распылению" энергии, что проявляется на практике в виде появления силы трения качения.
Качение идеального тела

Под идеальным телом в данном случае имеется в виду то, что оно является недеформируемым. В случае идеального колеса площадь его контакта с поверхностью равна нулю (оно касается поверхности вдоль линии).
Охарактеризуем силы, которые действуют на недеформируемое колесо. Во-первых, это две вертикальные силы: вес тела P и сила реакции опоры N. Обе силы проходят через центр масс (ось колеса), поэтому в создании крутящего момента не принимают участия. Для них можно записать:
P = N
Во-вторых, это две горизонтальные силы: внешняя сила F, которая толкает колесо вперед (она проходит через центр масс), и сила трения качения fr. Последняя создает крутящий момент M. Для них можно записать такие равенства:
M = fr*r;
F = fr
Здесь r - радиус колеса. Эти равенства содержат очень важный вывод. Если сила трения fr будет бесконечно малой, то она все равно создаст крутящий момент, который приведет к движению колеса. Поскольку внешняя сила F равна величине fr, то любое бесконечно малое значение F приведет к качению колеса. Это означает, что если тело качения является идеальным и не испытывает деформации в процессе движения, то ни о какой силе трения качения говорить не приходится.
Все существующие тела являются реальными, то есть испытывают деформацию.
Качение реального тела
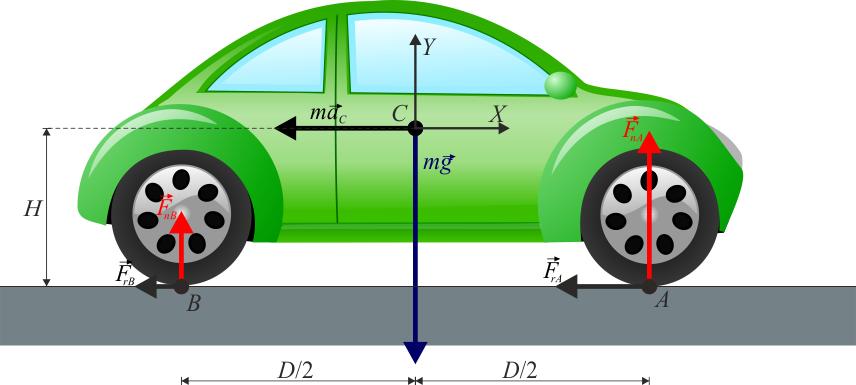
Теперь рассмотрим описанную выше ситуацию только для случая реальных (деформируемых) тел. Площадь касания колеса и поверхности уже не будет равна нулю, она будет иметь некоторое конечное значение.
Проведем анализ сил. Начнем с действия вертикальных сил, то есть веса и реакции опоры. Они по-прежнему равны друг другу, то есть:
N = P
Однако сила N теперь действует вертикально вверх не через ось колеса, а несколько смещена от нее на расстояние d. Если представить площадь соприкосновения колеса с поверхностью в виде площади прямоугольника, то длиной этого прямоугольника будет толщина колеса, а ширина будет равна 2*d.
Теперь перейдем к рассмотрению горизонтальных сил. Внешняя сила F по-прежнему не создает момента вращения и равна силе трения fr по абсолютной величине, то есть:
F = fr.
Момент сил, приводящий к вращению, будет создавать трение fr и реакцию опоры N. Причем эти моменты будут направлены в разные стороны. Соответствующее выражение имеет вид:
M = N*d - fr*r
В случае равномерного движения момент M будет равен нулю, поэтому получаем:
N*d - fr*r = 0 =>
fr = d/r*N
Последнее равенство с учетом записанных выше формул можно переписать так:
F = d/r*P
По сути, мы получили главную для понимания силы трения качения формулу. Далее в статье проведем ее анализ.
Коэффициент сопротивления качению
Этот коэффициент уже был введен выше. Также было дано геометрическое его объяснение. Речь идет о величине d. Очевидно, что чем больше эта величина, тем больший момент создает сила реакции опоры, который препятствует движению колеса.
Коэффициент сопротивления качению d, в отличие от коэффициентов трения покоя и скольжения, - величина размерная. Измеряется он в единицах длины. В таблицах его приводят обычно в миллиметрах. Например, для колес поезда, катящихся по стальным рельсам, d = 0,5 мм. Величина d зависит от твердости двух материалов, от нагрузки на колесо, от температуры и некоторых других факторов.
Коэффициент трения качения
Не нужно его путать с предыдущим коэффициентом d. Коэффициент трения качения обозначают символом Cr и вычисляют по следующей формуле:
Cr = d/r
Это равенство означает, что величина Cr является безразмерной. Именно она приводится в ряде таблиц, содержащих информацию о рассматриваемом виде трения. Этот коэффициент удобно использовать для практических расчетов, поскольку он не предполагает знания радиуса колеса.
Величина Cr в подавляющем большинстве случаев меньше, чем коэффициенты трения и покоя. Например, для автомобильных шин, движущихся по асфальту, величина Cr находится в пределах нескольких сотых (0,01 - 0,06). Однако она значительно возрастает при движении спущенных колес по траве и по песку (≈0,4).
Анализ полученной формулы для силы fr
Запишем еще раз полученную выше формулу силы трения качения:
F = d/r*P = fr
Из равенства следует, что чем больше диаметр колеса, тем меньшую силу F следует приложить, чтобы оно начало движение. Теперь запишем это равенство через коэффициент Cr, имеем:
fr = Cr*P
Как видно, сила трения прямо пропорциональна весу тела. Кроме того, при значительном увеличении веса P изменяется сам коэффициент Cr (он возрастает в виду увеличения d). В большинстве практических случаев Cr лежит в пределах нескольких сотых. В свою очередь, значение коэффициента трения скольжения лежит в пределах нескольких десятых. Поскольку для сил трения качения и скольжения формулы одинаковые, то качение оказывается выгодным с энергетической точки зрения (сила fr меньше на порядок силы скольжения в большинстве практических ситуаций).
Условие качения

Многие из нас встречались с проблемой проскальзывания колес автомобиля при движении по льду или по грязи. Почему это происходит? Ключ к ответу на этот вопрос лежит в соотношении абсолютных значений сил трения качения и покоя. Еще раз выпишем формулу для качения:
F ≥ Cr*P
Когда сила F будет больше или равна трению качения, тогда колесо начнет катиться. Однако если эта сила раньше превзойдет величину трения покоя, то раньше наступит проскальзывание колеса, чем его качение.
Таким образом, эффект проскальзывания определяется соотношением коэффициентов трения покоя и трения качения.
Способы противодействия проскальзыванию колеса автомобиля

Трение качения колеса автомобиля, находящегося на скользкой поверхности (например, на льду) характеризуется коэффициентом Cr = 0,01-0,06. Однако значения такого же порядка характерны для коэффициента трения покоя.
Чтобы избежать риска проскальзывания колеса, используют специальную "зимнюю" резину, в которую вкручены металлические шипы. Последние, врезаясь в ледяную поверхность, увеличивают коэффициент трения покоя.

Другой способ увеличение трения покоя заключается в модификации поверхности, по которой движется колесо. Например, с помощью посыпания ее песком или солью.