Чем старше становятся ученики, тем больше возникает потребность в скорости решения простых задач. На экзаменах дается не так много времени, чтобы подолгу решать простые примеры или задачи. Как найти диагональ квадрата быстро и легко? Это детям начинают преподавать с восьмого класса. В этой статье приведено два способа - один более длительный, другой - быстрее.
Как посчитать диагональ квадрата?
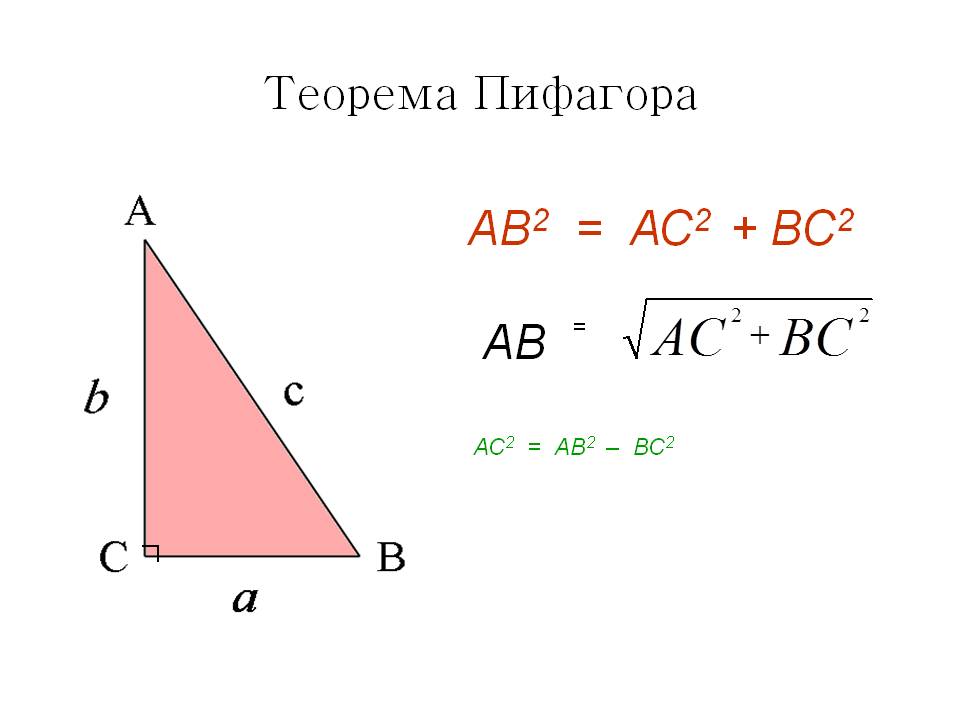
Первый способ - это всем уже известная и привычная теорема Пифагора. В квадрате все углы прямые, а значит, диагональ делит его на два равных прямоугольных треугольника и сама является их гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

Второй способ - это простая формула, которая свойственна исключительно квадратам, и ее нужно просто запомнить. Как известно, все стороны квадрата равны, и именно поэтому математики вычислили следующую формулу для нахождения его диагонали: она равна произведению стороны на корень из двух.
Безусловно, лучше всего просто запомнить формулу длины диагонали квадрата и пользоваться ею всегда, ведь это гораздо быстрее и удобнее. Особенно это чувствуется при решении задач в буквенном виде, где вместо целых больших подкорневых выражений можно обойтись лишь одним произведением.
Пример
Возьмем, к примеру, квадрат 6 на 6, то есть со стороной, равной шести сантиметрам.
По первому способу: пусть диагональ будет равна С, а боковая сторона - А.
Тогда получим, что С=√А^2+А^2 или С=√2А^2.
Запишем в числовом виде: С =√36 + 36. Получили √72, а это 3√8 или 6√2.
А теперь найдем ту же диагональ, но уже по второму способу: С = А√2 или в числовом виде: 6√2
Теперь видно, насколько второй способ быстрее, легче и самое главное - эффективнее, особенно в таких легких задачках, ведь на экзамене дорога каждая минута!
Другие свойства диагоналей квадрата
Помимо знания того, как найти диагонали квадрата, нужно также знать и их свойства. Основные из них:
- Диагонали равны между собой и точкой пересечения делятся пополам.
- При пересечении образуют прямые углы.
- Делят квадрат на равные треугольники.
Вывод
Вопросом, как посчитать диагонали квадрата, обычно задаются ученики, пропустившие эту тему в школе. Однако такие фундаментальные правила математики должен знать каждый! Желательно решать как можно быстрее, и для этого необходимы знания сокращенных формул. Все это предельно просто и легко, но вместе с тем является базой, необходимой для решения в дальнейшем гораздо более сложных задач. И важную часть этой базы занимает квадрат.




















