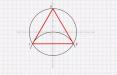
Деление окружности на равные части - классическая задача геометрии, известная еще со времен Евклида. Казалось бы, с помощью циркуля это легко сделать. Однако при ближайшем рассмотрении оказывается, что для правильного решения нужно хорошо понимать свойства окружности и уметь применять основные геометрические построения. В этой статье мы разберем один из частых случаев такой задачи - как разделить окружность на три равные части. Рассмотрим теоретическое обоснование и несколько практических способов решения с помощью циркуля и линейки. Это поможет решать не только данную конкретную задачу, но и глубже изучить свойства окружности, что пригодится на следующих этапах обучения геометрии.
Теоретические основы: как поделить окружность на 3 равные части
Для начала давайте разберемся, что означает разделение окружности на равные части с математической точки зрения. Важно понимать, что речь идет не просто о разделении линии окружности, а о разбиении круга, описанного этой окружностью, на секторы равной площади. Равенство площадей получившихся частей и есть ключевое условие задачи.
Чтобы разделить круг на n равных частей, нужно провести n радиусов так, чтобы между соседними радиусами был угол 360°/n. Тогда площадь каждого сектора будет равна S/n, где S - площадь всего круга. Это следует из основного свойства круга - пропорциональности длины дуги и величины центрального угла.
Для нашей конкретной задачи (как поделить окружность на 3 равные части), нужно разделить полный угол 360° на 3, получим 120°. Значит, надо провести три радиуса через каждые 120°.
Практические способы решения
Рассмотрим несколько практических способов, как поделить окружность на 3 равные части с помощью циркуля и линейки.
Способ с использованием углов 30° и 60°
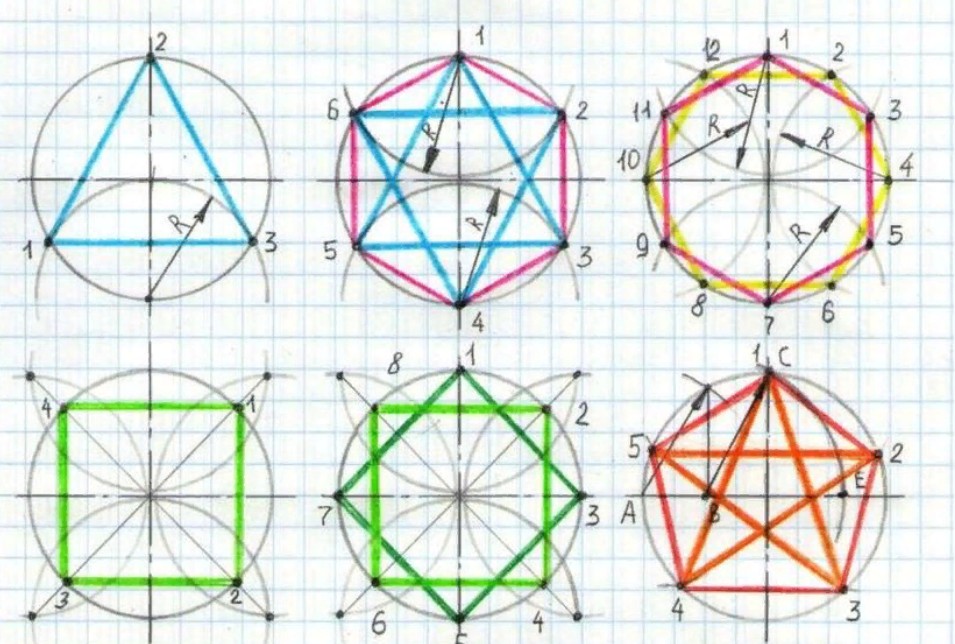
Этот способ основан на том, что угол 120° можно построить как сумму 30° и 60° углов. Сначала строим 30°, затем, не сдвигая циркуль, - 60°. Соединяем концы полученного угла 120° с центром окружности. Повторяем построение еще два раза через 120°.
Способ с построением правильного шестиугольника
Перед тем, как поделить окружность на 3 равные части, вспоминаем свойство правильного шестиугольника, вписанного в окружность. Строим окружность, затем шестиугольник. Соединяем его противоположные вершины - получаем три равных сектора.
Способ с использованием серединного перпендикуляра
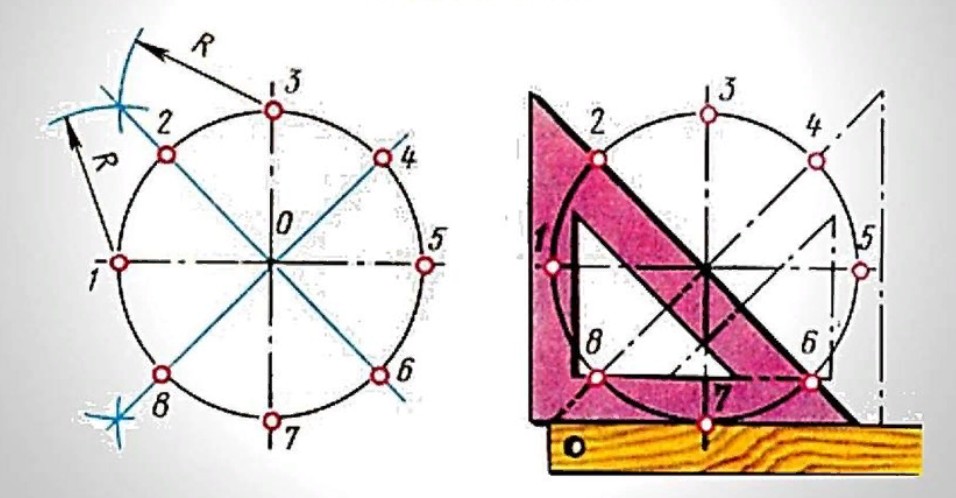
Строим произвольную окружность, отмечаем на ней две точки. Соединяем их и строим перпендикуляр. Повторяем это действие еще два раза с поворотом окружности на 120°.
Каждый из этих способов имеет свои особенности. Главное - четко представлять теоретическую базу и выполнять построения аккуратно. Тогда можно правильно разделить окружность на три равные части.
Применение на практике
Хотя задача кажется чисто теоретической, она применима в реальных ситуациях. Например, при разметке шкал приборов, делении циферблата часов, построении диаграмм. Важно понимать, как поделить окружность на 3 равные части для практического применения.
Обобщение на общий случай
Рассмотренные способы позволяют разделить окружность на любое число равных частей, не только на три. Достаточно построить соответствующие углы или многоугольники. Это расширяет возможности применения данного метода.
Историческая справка
Задача деления окружности восходит к работам древнегреческих математиков. Уже Евклид описал основные принципы такого деления. Эта задача стимулировала развитие геометрии и поиск новых инструментов.
Построение углов для деления окружности
Для деления окружности на равные части нужно уметь строить углы заданной величины. Это можно сделать с помощью угольника или транспортира. Однако есть и другие способы.
Например, угол 60° можно построить, отложив по окружности дугу, равную радиусу. А угол 30° получится, если отложить дугу, равную половине радиуса. Зная это, мы можем поделить окружность на 3 равные части, последовательно отложив дуги радиуса и полрадиуса.
Погрешность при делении окружности
При реальном выполнении построений всегда возникает погрешность из-за неточности инструментов и ошибок при черчении. Поэтому полученные части окружности могут быть не совсем равными.
Чтобы минимизировать эту погрешность, нужно максимально аккуратно выполнять все построения, проверять размеры отложенных отрезков и углов. Также имеет значение точность используемых инструментов.
Делим окружность на 3 равные части с помощью компьютера
Современные компьютерные программы для черчения позволяют легко и точно поделить окружность на любое число равных частей. Достаточно задать нужные параметры деления.
Это открывает дополнительные возможности для изучения свойств окружности. Можно быстро построить деление на большое количество частей, чего сложно добиться вручную.
Деление окружности на 3 равные части: проверка решения
Чтобы убедиться в правильности деления окружности, можно использовать разные способы проверки.
Можно вычислить длину получившихся дуг и убедиться в их равенстве. Или вычислить площади секторов по известным формулам. Также можно наложить построенные углы друг на друга и проверить их совпадение.
Обобщение задачи на пространственный случай
Аналогично окружности можно поделить сферу на равные части - сферические сегменты. Это имеет применение в стереометрии, при построении многогранников, в сферической тригонометрии.
Применение деления окружности в технике
Рассмотренные принципы деления окружности широко используются в различных областях техники.
Например, при проектировании циферблатов различных приборов - часов, амперметров, датчиков угла поворота. Деление окружности нужно для нанесения делений шкалы.
Деление окружности в строительстве и архитектуре
В строительстве деление окружности применяется при возведении круглых сооружений - резервуаров, силосных башен, водонапорных башен. Их поверхность часто разбивается на сегменты.

В архитектуре деление окружности используется при проектировании круглых зданий, ротонд, амфитеатров. Так определяются размеры секторов трибун, лож и т. д.
Деление окружности и картографические проекции
В картографии деление окружности применяется при построении различных проекций карт. Например, при азимутальных проекциях поверхность Земли делится на сегменты.
Связь с другими разделами математики
Задача о делении окружности связана с тригонометрией, геометрическими построениями, теорией пределов. Это позволяет применять для ее решения различные математические методы.
Обратная задача
Интересно также решать и обратную задачу: по заданным параметрам сегментов восстановить радиус всей окружности. Это требует применения обратных тригонометрических функций.
Автоматизация деления окружности
Современные компьютерные системы автоматического проектирования позволяют быстро выполнить деление окружности на любое число равных частей с высокой точностью.
Симметрия при делении окружности
При делении окружности на равные части важную роль играет симметрия. Получающиеся сегменты обладают осевой или центральной симметрией относительно радиусов.
Это свойство можно использовать для проверки правильности деления - сегменты должны быть симметричными отображениями друг друга.
Деление окружности в искусстве и дизайне
Принципы деления окружности широко применяются в искусстве и дизайне. Это позволяет гармонично сочетать элементы композиции.
Например, деление круга лежит в основе "золотого сечения". Симметричные узоры часто строятся на базе деления окружности.
Обобщения основной задачи
Исходную задачу можно обобщить, рассмотрев деление окружности на части в произвольном отношении. Это уже более сложная задача, требующая применения высшей математики.
Деление окружности в историческом аспекте
Задача деления окружности восходит еще к древнегреческой математике. Исторически ее решение стимулировало развитие геометрии.
Изучение работ античных математиков помогает лучше понять эволюцию методов деления окружности.
Сходство и различия разных способов деления
Рассмотренные способы решения базируются на общих принципах, но отличаются конкретной реализацией. Сравнивая их, можно глубже разобраться в задаче.
Возможные обобщения и аналоги задачи
Помимо упомянутых можно рассмотреть другие обобщения задачи: деление сферы, тора, конических сечений. Это позволит полнее изучить вопрос.
Аналогичные задачи возникают в проективной геометрии, при делении углов и отрезков.