Разность косинусов двух углов - распространенная операция в тригонометрии, позволяющая упростить сложные тригонометрические выражения. Она находит широкое применение при решении тригонометрических уравнений, преобразовании выражений, доказательстве тождеств и теорем. В данной статье мы подробно разберем, что представляет собой разность косинусов, как ее вычислять и где применять на практике.
Рассмотрим теоретические основы операции, этапы вычисления, приведем примеры и типовые задачи по применению разности косинусов в тригонометрии. Это поможет лучше понять суть данного математического инструмента и научиться использовать его с максимальной пользой.
Теоретические основы разности косинусов
Понятие «разность косинусов» основано на формуле разности двух косинусов. Эта формула позволяет перейти от разности cos α - cos β к произведению «косинус разности» и «косинус суммы» этих углов.
Формула разности косинусов имеет вид: cos α - cos β = -2 sin «косинус разности» ⋅ cos «косинус суммы», где «косинус разности» - это sin(α-β)/2, а «косинус суммы» - cos(α+β)/2.
Таким образом, разность косинусов двух углов равна произведению синуса полуразности этих углов на косинус полусуммы углов, взятому с отрицательным знаком.
Формула разности косинусов широко применяется для упрощения выражений, содержащих разность двух косинусов. Она также используется при решении тригонометрических уравнений и неравенств.
Пошаговый алгоритм вычисления разности
Для вычисления разности двух косинусов по формуле существует пошаговый алгоритм:
- Найти полусумму данных углов: (α + β)/2.
- Найти полуразность этих углов: (α - β)/2.
- Вычислить значения синуса и косинуса полученных полусуммы и полуразности.
- Подставить найденные значения синуса полуразности и косинуса полусуммы в формулу разности косинусов.
- Вычислить произведение и умножить его на -2. Полученный результат будет равен искомой разности косинусов.
- Разность косинусов вычислена.
Таким образом, для нахождения разности cos α - cos β нужно сначала найти «косинус разности» и «косинус суммы» этих углов, а затем подставить их в формулу и вычислить произведение.
Применение разности косинусов на практике
Разность косинусов часто применяется при решении тригонометрических уравнений. Например, если в уравнении стоит выражение вида cos a - cos b = c, то его можно преобразовать к виду:
-2·sin «косинус разности» · cos «косинус суммы» = c,
где вместо «косинус разности» и «косинус суммы» нужно подставить соответствующие выражения через данные углы a и b. После этого уравнение можно решить относительно неизвестного угла.
Также формула разности косинусов используется при вычислении значений тригонометрических функций. Если нужно найти cos a - cos b, а значения cos a и cos b неизвестны, можно воспользоваться алгоритмом вычисления разности косинусов.
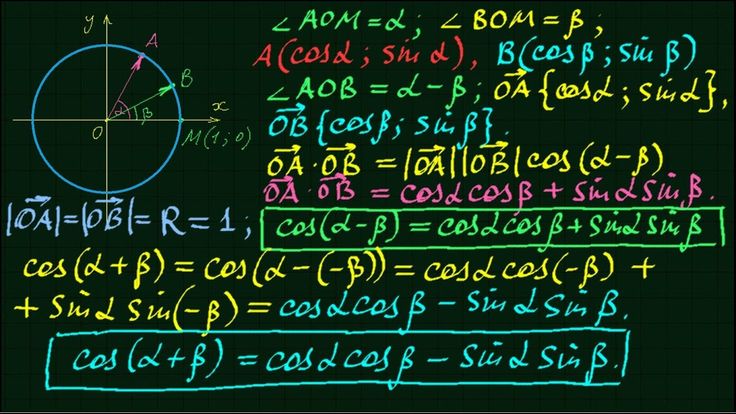
Разность косинусов в решении задач
Рассмотрим применение формулы разности косинусов при решении практических задач.
Например, нужно найти угол α, если известно, что cos(60° - α) = 0,5. Сначала применяем формулу разности косинусов:
cos(60° - α) = -2·sin(«косинус разности»)·cos(«косинус суммы»)
Где «косинус разности» - это (60° - α)/2 = 30° - α/2, а «косинус суммы» - (60° + α)/2 = 30° + α/2.
Подставляя это в формулу, получаем уравнение:
0,5 = -2·sin(30° - α/2)·cos(30° + α/2)
Решая которое, находим искомый угол α.
Также формула разности косинусов используется в задачах на нахождение расстояний, углов в треугольниках и многих других практических приложениях тригонометрии.






















