Возведение дроби в степень - одна из важнейших операций при работе с рациональными числами. Это позволяет упростить сложные дроби, решая уравнения и преобразуя выражения. Но часто возникают вопросы: как правильно возводить дробь в положительную или отрицательную степень? Что делать, если степень дробная или иррациональная? В этой статье мы детально разберем все правила и рассмотрим их применение на примерах.
Правила возведения простых дробей в натуральную степень
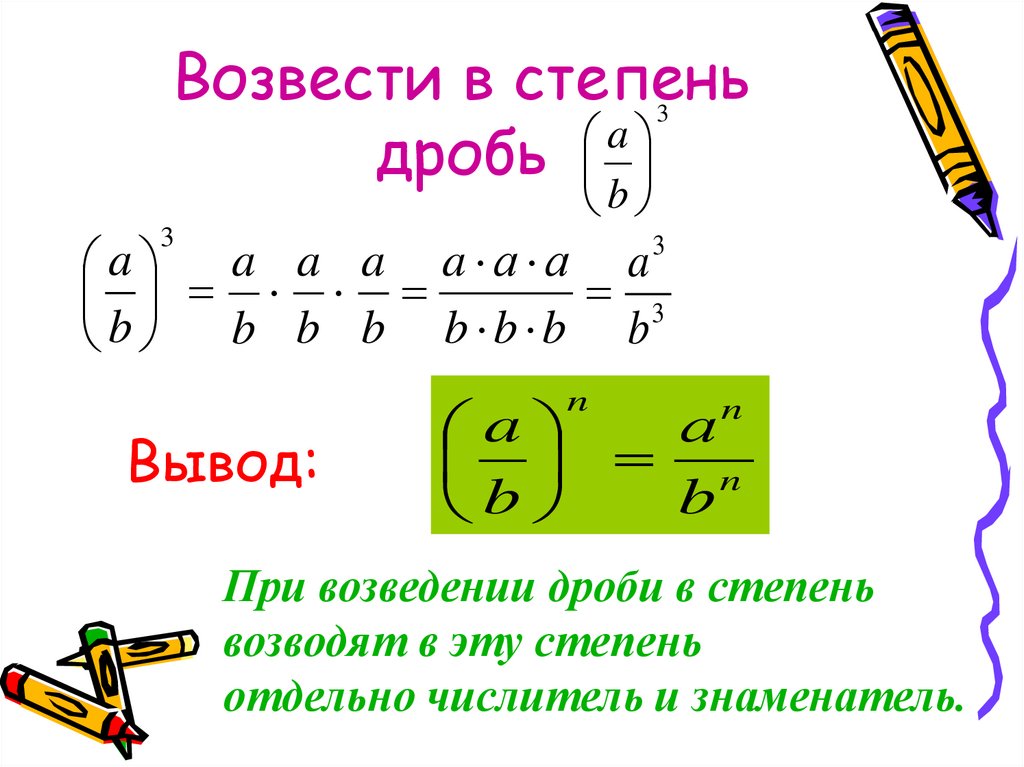
Чтобы правильно возвести простую дробь в натуральную степень, нужно следовать несложным правилам. Во-первых, возводятся в степень отдельно числитель и знаменатель. Во-вторых, при возведении в четную степень знаки минус исчезают. Рассмотрим подробнее на примерах.
Допустим, нужно возвести дробь (a/b)^n в натуральную степень n. Согласно первому правилу, сначала отдельно возводим в степень числитель и знаменатель: (a/b)^n = a^n / b^n. Например: (3/5)^2 = 3^2 / 5^2 = 9/25.
Если в дроби присутствует знак минус, то при возведении в четную степень он исчезает. Это второе правило. К примеру: (-2/3)^4 = (-2)^4 / 3^4 = 16/81. Минус исчез, так как 4 - четное число.
Теперь рассмотрим более сложный пример с многочленами: (x^2 - 3x + 1)/(2x + 5)^3. Согласно первому правилу возводим отдельно числитель и знаменатель: (x^2 - 3x + 1)^1 / (2x + 5)^3. Затем раскрываем скобки с помощью формул сокращенного умножения. В результате получаем: x^2 - 3x + 1 / (2x + 5)^3.
Подводя итог: чтобы правильно возвести простую дробь в натуральную степень, нужно применить два несложных правила - сначала отдельно возвести в степень числитель и знаменатель, затем учесть исчезновение минуса при возведении в четную степень. Следуя этим правилам, можно без ошибок справиться с возведением дробей в любую натуральную степень.
| Пример дроби | Дробь, возведенная в степень |
| (2/3)^2 | 4/9 |
| (-5/4)^3 | -125/64 |
Возведение отрицательных и дробных дробей в степень
Помимо натуральных степеней, дроби можно возводить и в отрицательные степени, и в дробные. Эти случаи требуют особых правил преобразования дробей перед возведением в степень. Рассмотрим подробно, как дробь возвести в отрицательную и дробную степень.
Чтобы возвести дробь в отрицательную степень, нужно сначала обратить эту дробь - поменять местами числитель и знаменатель. Затем полученную обратную дробь возводим в положительную степень по обычным правилам. Например, чтобы найти значение выражения (3/5)^{-2}, сначала обращаем дробь 3/5. Получаем 5/3. Затем возводим 5/3 во вторую степень: (5/3)^2 = 25/9. Итого: (3/5)^{-2} = 25/9.
При возведении дробей в дробные степени используется операция извлечения корня. Числитель и знаменатель исходной дроби извлекаются в корни степеней, соответствующих знаменателю и числителю степени. Например, чтобы найти значение (2/5)^(3/2), извлекаем корень квадратный из числителя 2 и корень кубический из знаменателя 5: (2)^(1/2) / (5)^(1/3) = √2/√[5].
Обратите внимание, если под корнем стоит отрицательное число, то нужно брать модуль этого числа, а перед корнем поставить знак минус. К примеру: (-8/27)^(1/3) = -√[|(-8)|] / 3 = -2/3. Здесь сначала взяли модуль отрицательного числителя -8, затем извлекли корень, поставив снаружи знак минус.
Иногда перед возведением дроби в дробную степень нужно выполнить преобразования с помощью свойств степени. Рассмотрим пример: (x^3 / 9y)^(2/3). Сначала перенесем степень 2/3 только на x: (x^3)^(2/3) / (9y)^(2/3). Затем применим свойство степени степени: (x^3)^(2/3) = x^(3*(2/3)) = x^2. Итого: x^2 / (9y)^(2/3).






















