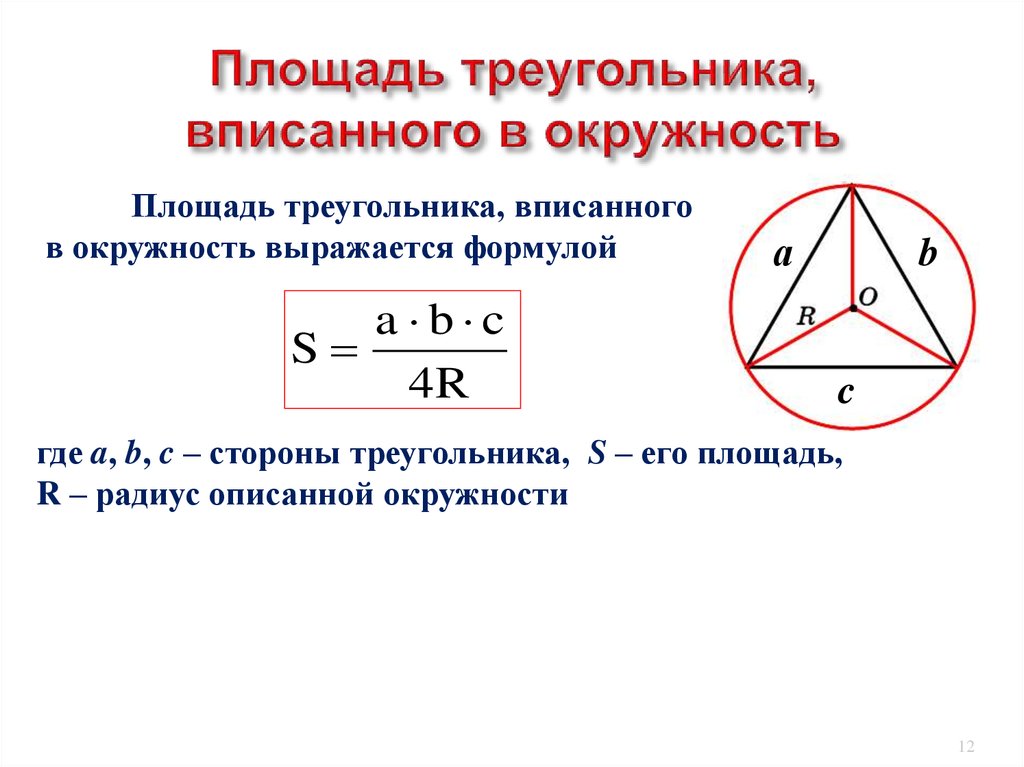
Вписанный треугольник - это треугольник, в который вписана окружность, касающаяся всех трех его сторон. Нахождение площади такого треугольника имеет большое практическое значение в геометрии, архитектуре, строительстве и других областях.
Формулы для нахождения площади вписанного треугольника
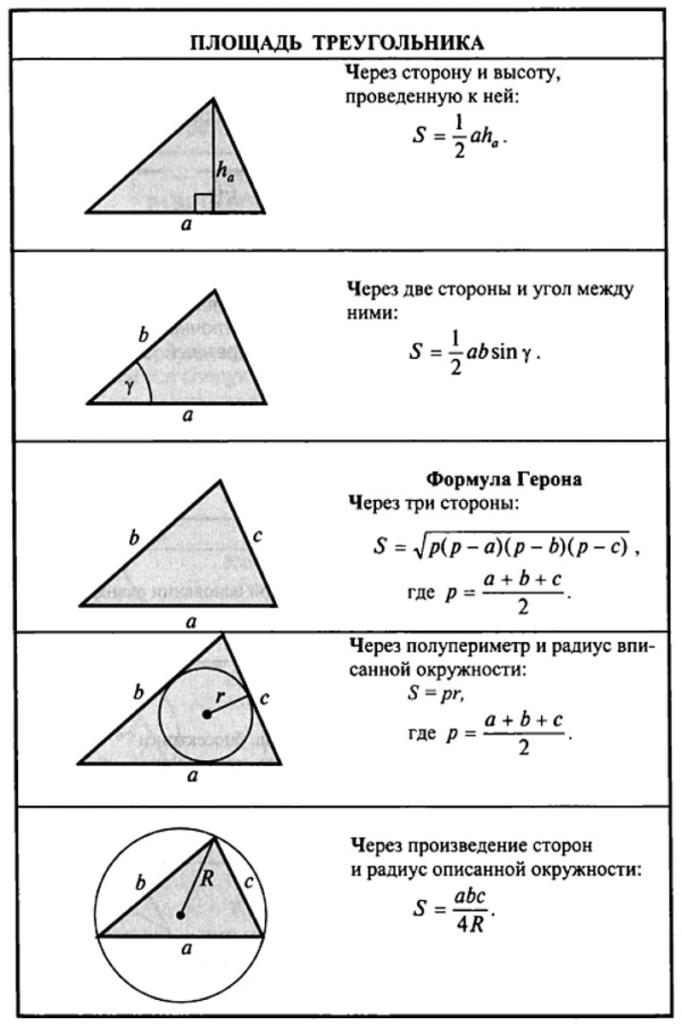
Существует несколько формул, с помощью которых можно найти площадь вписанного треугольника в зависимости от известных данных:
- Если известен радиус
rвписанной окружности и полупериметрpтреугольника, тоS = pr, где S - площадь треугольника. - Если известны длины трех сторон треугольника
a,b,c, то площадь равнаS = √(s - a)(s - b)(s - c), гдеs = (a + b + c) / 2- полупериметр. - Для правильного треугольника со стороной
aплощадь равнаS = (a2√3) / 4.
Примеры применения формул
Рассмотрим конкретные примеры нахождения площади вписанного треугольника с использованием различных формул.
Пример 1. Площадь через радиус
Дан вписанный треугольник ABC с полупериметром 10 см. Радиус вписанной окружности равен 4 см. Найти площадь треугольника ABC.
Решение:
Из условия: p = 10 см, r = 4 см. По формуле S = pr: S = 10 * 4 = 40 см2
Ответ: 40 см2.

Пример 2. Правильный треугольник
Дан правильный треугольник ABC с длиной стороны, равной 8 см. В него вписана окружность. Найти площадь.
Решение: Формула площади правильного треугольника: S = (a2√3) / 4 где a = 8 см. Подставляя: S = (82 * √3) / 4 = 27,7 см2
Ответ: 27,7 см2

Пример 3. Прямоугольный треугольник
В прямоугольный треугольник ABC вписана окружность радиусом 5 см. Катеты 12 и 16 см. Найти площадь ABC.
Решение: Катеты: a = 12 см, b = 16 см. Радиус окружности: r = 5 см. По теореме Пифагора: c = √(a2 + b2) = 20 см. Полупериметр: p = (a + b + c) / 2 = 24 см. По формуле площади: S = pr = 24 * 5 = 120 см2.
Ответ: 120 см2
Зависимость площади от радиусов вписанных окружностей
Интересный факт: если в треугольник последовательно вписать две окружности разного радиуса r1 и r2 (касающиеся сторон треугольника), то отношение площадей этих окружностей всегда будет равно отношению квадратов радиусов:
S1 / S2 = (r1 / r2)2
Это объясняется тем, что площади окружностей пропорциональны квадратам их радиусов согласно формуле S = πr2.
Применение
Информация о площади вписанного треугольника используется:
- В геодезии и землеустройстве.
- В архитектуре и строительстве.
- При нахождении площади вписанного круга.
- В математике для доказательства теорем.
Зная формулы и умея их применять, можно с легкостью находить площадь любого вписанного треугольника.
Другие способы нахождения площади вписанного треугольника
Помимо рассмотренных выше формул, существуют и другие способы вычисления площади вписанного треугольника.
Использование теоремы синусов
Если известны две стороны треугольника a и b, а также угол между ними C, можно воспользоваться теоремой синусов:
S = (1/2) * a * b * sin(C)
Этот способ удобен, когда известны конкретные стороны и угол треугольника, но неизвестен его полупериметр.
Задача: найдите площадь правильного треугольника, вписанного
Для нахождения площади правильного вписанного треугольника также можно использовать радиус r вписанной в него окружности:
S = (√3/4)*r2
Эта формула выводится на основании свойств правильного треугольника и позволяет легко найти его площадь, зная лишь радиус вписанной окружности.
Задача: найдите площадь по двум сторонам и углу между ними
Еще один распространенный в геометрии способ - использование двух сторон a, b и угла между ними C. Тогда площадь вычисляется по теореме синусов:
S = (1/2)*a*b*sin(C)
Это наиболее универсальный метод, применимый к любым треугольникам при наличии данных об а, b и C.
Через стороны и высоты треугольника
Еще один способ - использование сторон и высот треугольника. Пусть a, b, c - стороны, ha, hb, hc - высоты. Тогда:
S = (1/2)(a*ha + b*hb + c*hc)
Этот метод применим, когда известны конкретные стороны и высоты к ним.
По координатам вершин треугольника
Если известны координаты вершин треугольника (xA, yA), (xB, yB) и (xC, yC), то площадь вычисляется по формуле:
S = abs((xB - xA)*(yC - yA) - (xC - xA)*(yB - yA))/2
Где abs() - модуль числа. Этот метод используется в аналитической геометрии.
Выводы
Итак, существует множество различных формул и теорем для нахождения площади вписанного треугольника в зависимости от известных исходных данных. Владение этим математическим аппаратом позволяет решать широкий круг геометрических задач на вычисление площадей.
Вычисление площади треугольника графическим способом
Помимо аналитических формул, существует графический способ нахождения площади вписанного треугольника с помощью разбиения его на более простые фигуры.
Разбиение на прямоугольные треугольники
Любой треугольник можно разбить на два прямоугольных треугольника, соединив одну из вершин с точкой пересечения медиан. Зная длины катетов и гипотенуз этих треугольников, по теореме Пифагора находим площади каждого из них, а затем суммируем.
Разбиение на произвольные треугольники
Также можно разбить исходный треугольник на произвольное число меньших треугольников, соединяя различные точки внутри него. Для каждого полученного треугольника находим площадь по имеющимся данным, а затем суммируем.
Метод трапеций
Этот метод заключается в дополнении исходного треугольника до трапеции с параллельными основаниями, для которой легко найти площадь. Зная площадь трапеции и дополнительного треугольника, находим площадь исходного.
Метод палетки
Наиболее наглядный способ - наложение на треугольник палетки из клеток одинакового размера. Подсчитывая число целых и долевых клеток внутри треугольника, можно найти приближенное значение его площади.
Проверка найденного результата
Чтобы убедиться в правильности полученного графическим способом значения площади вписанного треугольника, рекомендуется вычислить ее по известным аналитическим формулам и сравнить результаты.
Значительное расхождение говорит о возможной ошибке при использовании графических методов. Небольшая погрешность объясняется приближенным характером графических измерений.
Вычисление площади треугольника графическим способом
Разбиение на прямоугольные треугольники
Любой треугольник можно разбить на два прямоугольных треугольника, соединив одну из вершин с точкой пересечения медиан. Зная длины катетов и гипотенуз этих треугольников, по теореме Пифагора находим площади каждого из них, а затем суммируем.
Метод трапеций
Этот метод заключается в дополнении исходного треугольника до трапеции с параллельными основаниями, для которой легко найти площадь. Зная площадь трапеции и дополнительного треугольника, находим площадь исходного.



























