Четырехугольники - один из самых распространенных видов многоугольников. Мы сталкиваемся с ними повсюду: дома, на работе, на улице. Давайте разберемся, что такое четырехугольник, какие бывают его виды и свойства.
Определение четырехугольника
Четырехугольник - это многоугольник, у которого четыре стороны. Это означает, что у него имеется ровно четыре вершины и четыре стороны, соединяющие эти вершины. При этом никакие три вершины четырехугольника не лежат на одной прямой.
Количество вершин четырехугольника всегда равно четыри. Это следует из определения.
У четырехугольника различают:
- Стороны - отрезки, соединяющие вершины
- Углы - углы при вершинах четырехугольника
- Диагонали - отрезки, соединяющие противоположные вершины четырехугольника (их может быть одна или две)
По внешнему виду четырехугольники делятся на выпуклые и невыпуклые.
Выпуклый четырехугольник - такой четырехугольник, у которого при проведении прямой через любые три точки четырехугольника (вершины или точки на сторонах) эти три точки лежат по одну сторону от прямой.
Для вычисления площади произвольного четырехугольника используется формула:
| S = 1⁄2(a·h + b·c) |
где S - площадь четырехугольника, a и b - стороны основания, h - высота, опущенная на сторону a, c - вторая высота четырехугольника.
Существует несколько основных видов четырехугольников. Рассмотрим некоторые из них.
Параллелограмм
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. К основным свойствам параллелограмма относят:
- Противоположные стороны равны
- Диагонали взаимно пересекаются в середине
- Диагонали делят параллелограмм на четыре равных треугольника
Существует три основных признака параллелограмма:
- Если две стороны параллельны, а две другие равны
- Если диагонали взаимно пересекаются в середине
- Если диагонали делят четырехугольник на четыре равных треугольника
Прямоугольник
Прямоугольник - это параллелограмм, у которого все углы прямые. Значит, у него есть все свойства параллелограмма, но дополнительно выполняется равенство каждого угла 90 градусам.
Ромб
Ромб - это параллелограмм, у которого все стороны равны. Как и у всех параллелограммов, у ромба противоположные стороны параллельны, а диагонали взаимно перпендикулярны.
Правильный четырехугольник
Правильным называют такой четырехугольник, у которого все стороны и все углы равны. Это означает, что каждый угол в нем равен 90 градусам, а значит, правильный четырехугольник всегда является квадратом.
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие - нет. Параллельные стороны трапеции называются основаниями.
Различают равнобедренную трапецию, у которой боковые стороны равны, и прямоугольную трапецию, имеющую прямой угол.
Формулы площадей четырехугольников
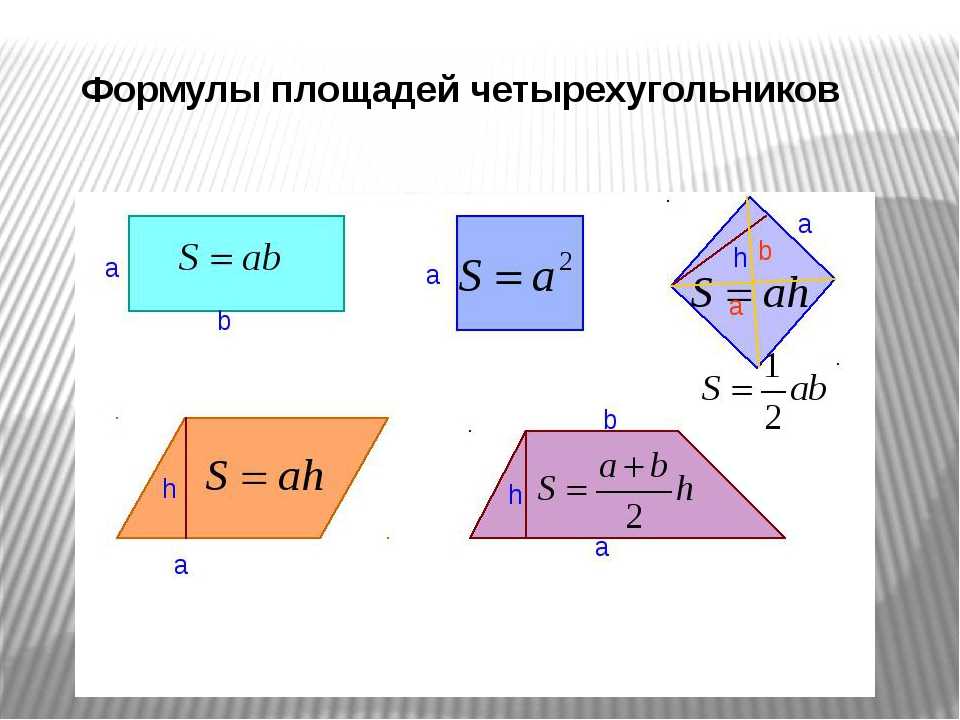
Для вычисления площадей разных видов четырехугольников используются следующие формулы:
- Площадь параллелограмма: S = ab, где a и b - основания параллелограмма
- Площадь ромба: S = pq/2, где p и q - диагонали ромба
- Площадь квадрата: S = a2, где а - сторона квадрата
Для большинства четырехугольников можно также использовать формулу, приведенную ранее для общего случая:
S = 1⁄2(a·h + b·c)
Таким образом, зная основные параметры четырехугольника, можно вычислить его площадь при помощи соответствующей формулы.
Четырехугольники в природе и архитектуре
В природе можно встретить много примеров четырехугольников и их разновидностей:
- Листья клена, дуба, каштана часто имеют форму вытянутых четырехугольников
- У многих насекомых (жуков, бабочек) тело или крылья образуют четырехугольную форму
- Соты в ульях - это множество правильных шестиугольников, которые в совокупности образуют четырехугольную конструкцию
- Муравейники и термитники также напоминают четырехугольные здания с многочисленными ответвлениями и переходами
В архитектуре четырехугольные формы используются повсеместно.
Применение в строительстве:
- Здания и сооружения чаще всего имеют прямоугольную или квадратную форму в плане
- Кирпичи, блоки, плитки - основные строительные материалы, имеющие форму прямоугольного параллелепипеда
Использование в дизайне интерьеров:
- Прямоугольные окна, дверные проемы
- Потолочные светильники и люстры часто имеют четырехугольную или квадратную форму
- Кафельная плитка на полах и стенах - различные виды четырехугольников
Применение в производстве:
Четырехугольные заготовки удобны для раскроя на детали при производстве:
- Мебели
- Бытовой техники
- Тары и упаковки

Решение задач на практике
Знания свойств четырехугольников помогают решать различные практические задачи:
- Вычислять perimeter и площадь участков
- Подбирать нужное количество плитки для облицовки
- Экономно раскраивать рулоны обоев или ткани
Построение четырехугольника
Для построения четырехугольника на плоскости используются следующие инструменты:
- Линейка
- Угольник
- Циркуль
- Транспортир
Построение по заданным сторонам
Если известны длины всех сторон четырехугольника, то:
- Проводим произвольную сторону AB заданной длины
- Из точки B проводим сторону BC заданной длины
- Из точки C проводим сторону CD заданной длины
- Соединяем точки A и D отрезком, получаем искомый четырехугольник ABCD
Построение по заданным углам
Если известны величины углов четырехугольника, то:
- Проводим две пересекающиеся прямые под заданным углом
- Откладываем остальные углы и получаем вершины четырехугольника
- Соединяем вершины отрезками, получаем искомый четырехугольник
























