Геометрия - фундаментальная наука, изучающая пространственные формы и отношения. Одним из важнейших понятий геометрии является перпендикулярность. Знание определения перпендикуляра позволяет решать множество геометрических задач. Давайте разберемся, что такое перпендикуляр в геометрии.
1. Определение понятия "перпендикуляр"
Перпендикулярность - это взаимное расположение двух объектов (отрезков, прямых, плоскостей) под прямым углом друг к другу. Рассмотрим разные виды перпендикулярности более подробно.
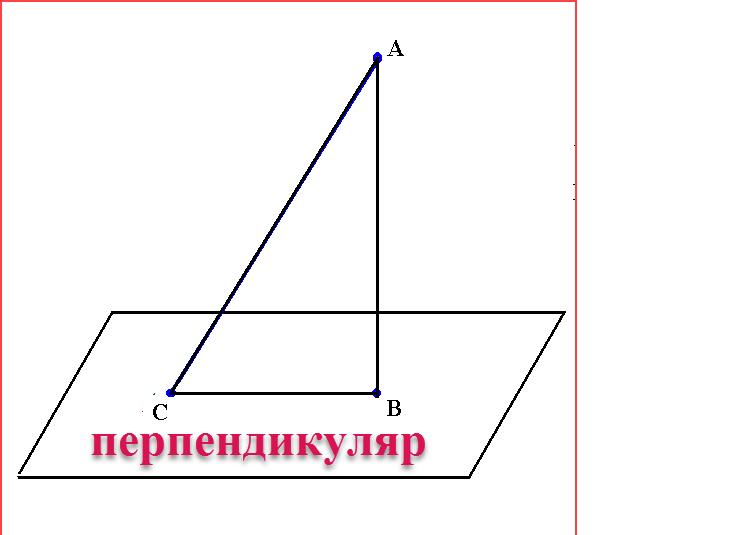
1.1. Перпендикулярные прямые: определение, свойства
Две прямые на плоскости называются перпендикулярными, если при их пересечении образуются четыре прямых угла. Это означает, что каждый из углов равен 90 градусов.
Основное свойство перпендикулярных прямых:
- Через точку, лежащую вне прямой, можно провести прямую, перпендикулярную данной, и притом только одну
Перпендикулярные прямые широко используются в геометрии, например при доказательстве теорем и решении множества практических задач.
1.2. Перпендикуляр к прямой: определение, построение, теорема о единственности
Перпендикуляром к прямой называется отрезок прямой, перпендикулярный к данной прямой, один из концов которого лежит на данной прямой. Этот конец отрезка называется основанием перпендикуляра.
Доказана теорема, что из точки, не лежащей на данной прямой, к этой прямой можно провести только один перпендикуляр. Это позволяет однозначно определять кратчайшее расстояние от точки до прямой.
Перпендикуляр к прямой применяется в геометрических построениях, а также для вычисления расстояний. Например, можно найти расстояние от точки до плоскости как длину опущенного из этой точки перпендикуляра.
1.3. Другие виды перпендикуляров: к плоскости, между плоскостями. Свойства
Помимо перпендикулярности между прямыми, существует понятие перпендикуляра к плоскости и перпендикулярности между плоскостями.
Перпендикуляром к плоскости называется прямая, перпендикулярная ко всем прямым, лежащим в данной плоскости.
А две плоскости называются перпендикулярными, если все прямые одной плоскости перпендикулярны всем прямым другой плоскости.
1.4. Построение перпендикуляра к прямой
Рассмотрим, как можно построить перпендикуляр к прямой в геометрии. Существует простой способ.
С помощью угольника. Прикладываем к прямой угол 90 градусов угольника и проводим прямую из заданной точки.
Таким образом, перпендикуляр к прямой можно построить из точки, не лежащей на этой прямой, с помощью основных чертежных инструментов.
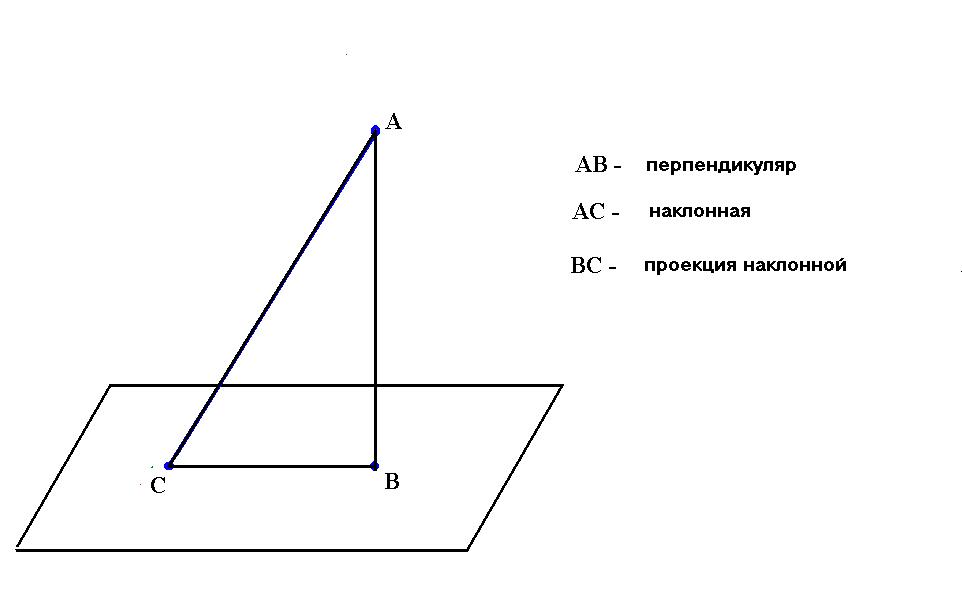
1.5. Теорема о трех перпендикулярах и ее применение
Одной из важных теорем, связанных с перпендикулярами, является теорема о трех перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.
Это означает, что если к основанию наклонной провести перпендикуляр к ее проекции, то получится перпендикуляр и к самой наклонной.
Данная теорема используется при доказательстве многих утверждений в геометрии. Например, она позволяет упростить нахождение угла между прямой и плоскостью, определение расстояния между скрещивающимися прямыми.
1.6. Применение перпендикулярности в технике и архитектуре
Помимо решения геометрических задач, перпендикулярность широко используется в технике, строительстве, архитектуре. Рассмотрим несколько примеров.
- Конструкция стола или стула предполагает соединение ножек перпендикулярно к столешнице или сидению для обеспечения устойчивости.
- В токарном станке инструмент перемещается строго перпендикулярно оси вращения заготовки, чтобы обеспечить правильную геометрическую форму детали после обработки.
- При возведении высотных зданий стены соединяются перпендикулярно к фундаменту, чтобы равномерно распределить нагрузку по всему зданию.
Таким образом, перпендикулярность лежит в основе устойчивости и прочности многих технических конструкций и архитектурных решений.
В статье подробно рассматривалось определение перпендикуляра в геометрии. Разбирались различные виды перпендикулярности: между отрезками, прямой и плоскостью, а также между плоскостями. Приведены теоремы о перпендикулярах и их применение при решении геометрических задач и в технике. Были даны практические рекомендации по построению перпендикуляра к прямой, которые позволят легко решать многие геометрические задачи.






















