Подобные треугольники - одно из фундаментальных понятий геометрии. Это треугольники, которые имеют одинаковую форму, но разные размеры. Изучение свойств таких треугольников позволяет решать множество задач на вычисление длин, углов, площадей. Давайте разберемся подробнее, что представляют собой подобные треугольники, каковы их основные признаки и свойства.
Определение подобных треугольников
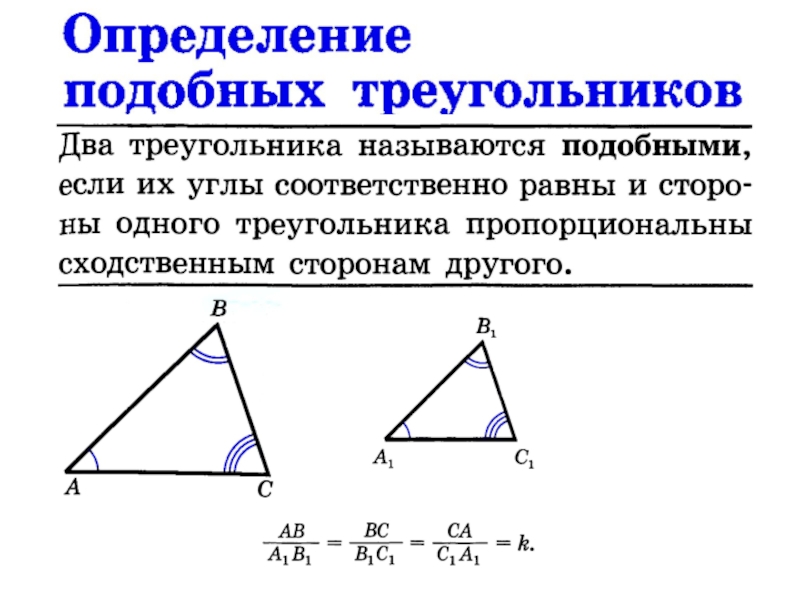
Два треугольника называются подобными, если их углы попарно равны, а стороны пропорциональны. Формально это можно записать так:
- ∠A = ∠A1
- ∠B = ∠B1
- ∠C = ∠C1
и
- AB / A1B1 = const
- BC / B1C1 = const
- AC / A1C1 = const
Здесь A1B1C1 - второй подобный треугольник, AB, BC, AC - стороны первого, A1B1, B1C1, A1C1 - стороны второго.
Константа, равная отношению сторон подобных треугольников, называется коэффициентом подобия и обозначается буквой k:
Стороны подобных треугольников, лежащие напротив равных углов, называются сходственными. На рисунке сходственными являются стороны AB и A1B1, BC и B1C1, AC и A1C1.
Основные свойства подобных треугольников
Из определения подобных треугольников вытекает два важных свойства:
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия:
- Любые характерные отрезки (медианы, биссектрисы, высоты) также пропорциональны с коэффициентом подобия k.
Эти два свойства часто используются при решении геометрических задач с подобными треугольниками.
Признаки подобия треугольников
Существует три основных признака, позволяющих установить подобие двух треугольников без вычисления всех элементов:
- Первый признак: если два угла одного треугольника равны двум углам другого, то такие треугольники подобны:
- Второй признак: если две стороны одного треугольника пропорциональны двум сторонам другого, а углы между ними равны, то треугольники подобны:
- Третий признак: если все три стороны одного треугольника пропорциональны всем трем сторонам другого, то такие треугольники подобны:
Эти признаки вытекают из определения подобных треугольников и часто используются на практике для доказательства подобия. Рассмотрим несколько примеров их применения.

Типичные случаи подобия треугольников
Кроме общих признаков подобия, существует несколько типичных случаев, когда можно без доказательств утверждать, что два треугольника подобны:
- Если к стороне треугольника провести параллельную прямую, то отсеченный при этом треугольник будет подобен исходному:
- В трапеции, которая разбита диагональю на два треугольника, эти треугольники подобны между собой:
- В прямоугольном треугольнике малые треугольники, отсеченные высотой, подобны исходному:
Эти частные случаи хорошо запоминать, поскольку они часто встречаются на практике. Рассмотрим несколько примеров их использования для решения задач.
Вычисление углов подобных треугольников
Еще одно важное применение свойств подобных треугольников - это нахождение неизвестных углов. Используем для этого признаки подобия:
Например, в ∆ABC угол C равен 40°, в подобном ему ∆A1B1C1 угол C1 равен 60°. Найти угол B.
Решение: По условию, ∆ABC ~ ∆A1B1C1. Следовательно, по первому признаку подобия соответственные углы равны:
- ∠A = ∠A1
- ∠B = ∠B1
- ∠C = ∠C1
Подставляя известные углы C и C1, получаем: ∠B = ∠B1 = 60°.
Ответ: угол B равен 60 градусов.
Определение подобных треугольников
Дайте определение подобных треугольников.
Подобными называются треугольники, у которых соответственные углы равны, а стороны пропорциональны. Иными словами, подобные треугольники имеют одинаковую форму, но разные размеры. Формально:
где ∆ABC и ∆A1B1C1 - подобные треугольники, AB, BC, AC и A1B1, B1C1, A1C1 - их стороны.
Применение подобия при решении практических задач
Помимо основных геометрических задач на вычисление площадей, углов и длин, свойства подобных треугольников применяются во многих практических ситуациях:
- В архитектуре и строительстве при возведении сооружений в уменьшенном или увеличенном масштабе
- В изобразительном искусстве при построении композиции картины с соблюдением пропорций объектов
- В физике при моделировании различных явлений и процессов
Рассмотрим несколько примеров такого рода задач и способы их решения с использованием подобия треугольников.
Задачи с подобными треугольниками в архитектуре
При проектировании архитектурных сооружений часто приходится сталкиваться с задачами масштабирования. Например, по известным размерам реального здания требуется построить его макет в заданном масштабе.
В таких случаях на помощь приходят свойства подобия треугольников. Рассмотрим конкретный пример.
Пример: построение макета здания в масштабе
Дан чертеж фасада здания в натуральную величину. Требуется построить макет этого фасада в масштабе 1:100. Размеры на чертеже: высота здания - 25 м, длина фасада - 15 м.
Решение:
- Определяем размеры макета по масштабу:
- Высота макета = 25 м / 100 = 0,25 м Длина макета = 15 м / 100 = 0,15 м
- Строим макет с полученными размерами. Получаем уменьшенную, но подобную копию реального фасада здания.
Подобие в скульптуре и лепке
Создание скульптур и лепка требуют тщательного соблюдения пропорций. Знание законов подобия помогает как при уменьшении, так и при увеличении масштабов.
Моделирование физических процессов
Подобие широко используется в физике при моделировании различных процессов - от строения атома до космических явлений. Принцип: явления протекают аналогично в подобных системах.
























