Нормаль - удивительное геометрическое понятие, которое на первый взгляд кажется простым, но при ближайшем рассмотрении обнаруживает множество тонкостей и особенностей. Давайте разберемся, что же из себя представляет нормаль в математике и где она применяется.
Определение нормали
Формально нормаль - это вектор, перпендикулярный касательному пространству кривой или поверхности в данной точке. Конкретнее:
- Для плоской кривой нормаль лежит в плоскости самой кривой;
- Для пространственной кривой существует целая нормальная плоскость;
- Для поверхности нормаль однозначно определена в каждой точке.
Таким образом, нормаль - это некая "опора", "стержень" объекта в данной точке. Зная направление нормали, можно судить, как объект "опирается" на окружающее пространство.
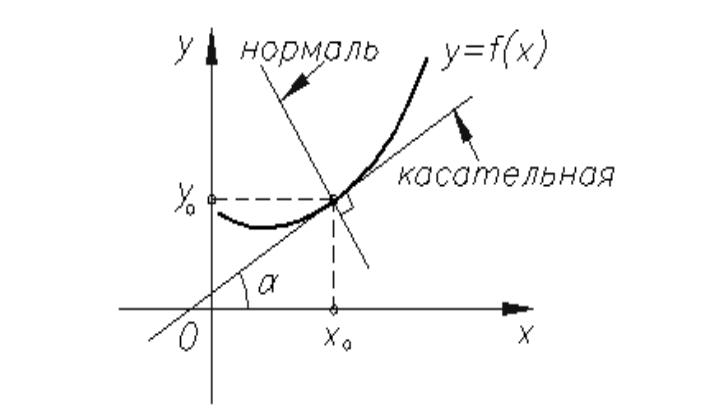
Как вычислить нормаль
Вычислить нормаль несложно, если известно уравнение кривой или параметрические уравнения поверхности. Рассмотрим пример для кривой на плоскости.
Пусть кривая задана уравнением y = f(x). Тогда нормаль имеет уравнение:
(x - x0) + (y - y0)f'(x) = 0
где x0, y0 - текущая точка на кривой, а f'(x) - производная функции f(x) в этой точке. Как видно из формулы, для вычисления нормали достаточно найти производную.
Нормаль - это на самом деле очень важное понятие в геометрии, позволяющее решать множество задач.
Далее давайте разберем основные свойства нормалей.
Свойства нормалей
Любая нормаль обладает следующими свойствами:
- Нормаль всегда перпендикулярна касательной в данной точке;
- Длина нормали не имеет принципиального значения, важно лишь направление;
- У плоских и гладких кривых нормаль однозначно определена в каждой точке;
- Нормали двух пересекающихся кривых (или поверхностей) образуют угол, равный углу пересечения самих объектов.
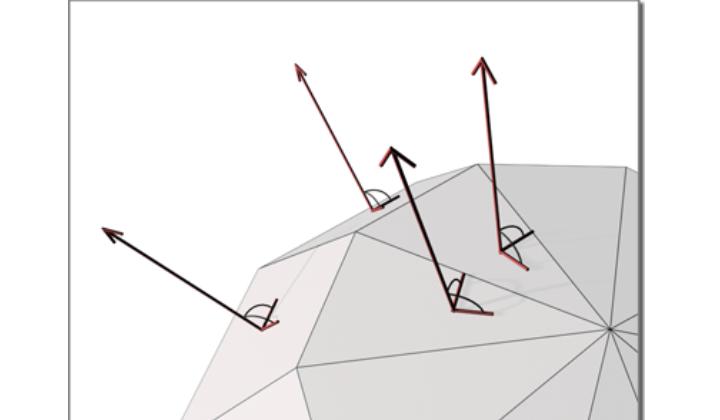
Эти свойства позволяют эффективно использовать нормали при решении множества геометрических, физических и инженерных задач. Рассмотрим некоторые из них.
Где используются нормали
Нормаль к поверхности широко применяется в следующих областях:
- Геометрическая оптика - отражение и преломление лучей;
- Компьютерная графика - визуализация объемных моделей;
- Физика - движение частиц в потенциальных полях;
- Инженерия - моделирование сложных поверхностей.
Конкретные примеры применения нормалей:
- Моделирование лучей света при проектировании оптических систем;
- Расчет траектории частицы в электростатическом поле конденсатора;
- Построение реалистичных 3D-моделей в компьютерных играх и анимации.
Как видно, область применения нормалей весьма широка. По сути, везде, где нужно работать с гладкими поверхностями или траекториями, требуется рассчитывать нормали. В дальнейшем мы еще вернемся к вопросу использования нормалей на практике.





















