Понятие отрезка является одним из фундаментальных в геометрии. Отрезки составляют основу многих геометрических фигур. Знание свойств отрезков позволяет решать множество практических задач. В этой статье мы подробно разберем, что такое отрезок, как определяется и вычисляется его длина, а также приведем примеры применения этих знаний на практике.
Определение отрезка
Давайте начнем с самого базового - что же такое отрезок:
- Отрезок - это часть прямой, ограниченная с двух сторон точками.
- Точки, ограничивающие отрезок, называются концами отрезка.
- Отрезок принято обозначать двумя заглавными буквами латинского алфавита, которые ставятся при его концах. Например: AB.
Отрезок AB тот же самый, что и отрезок BA - просто записано в другом порядке. Главное правило такое: любые две точки определяют один и только один отрезок. То есть, сколько бы раз мы ни соединяли точки A и B, получится всегда один и тот же уникальный отрезок AB.
Свойства отрезков
У отрезков есть несколько важных свойств, которые надо знать:
- Одна и та же точка может принадлежать сразу нескольким отрезкам.
- Любая точка по отношению к отрезку может либо лежать на нем, либо находиться снаружи. На рисунке точка E лежит на отрезке AB, а точки F и G - снаружи.
- Отрезок можно разделить на части с помощью дополнительных точек. Получившиеся части всегда будут короче исходного отрезка.
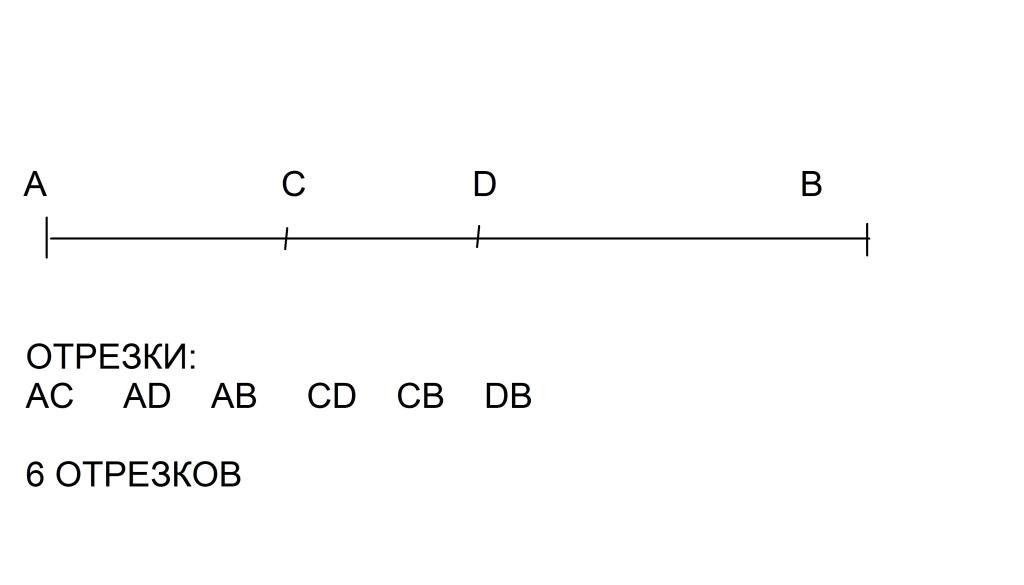
На данном рисунке отрезок AB разбит точками C и D на 5 части: AC, AD, CD, CB и DB. Каждая из этих частей меньше всего отрезка AB.
Длина отрезка
Важнейшей характеристикой отрезка является его длина. Длина отрезка - это расстояние между его концами или, другими словами, протяженность отрезка.
Чтобы выразить длину отрезка числом, нужно выбрать единицы измерения. Чаще всего используют такие единицы как миллиметр, сантиметр, дециметр, метр и километр.
Например, если расстояние между концами отрезка равно 5 сантиметрам, то записывают:
Длина отрезка AB = 5 см
Существует формула для вычисления длины отрезка L = n * l, где:
- L - длина отрезка;
- n - количество единичных отрезков, уложившихся в нем;
- l - длина одного единичного отрезка в выбранных единицах измерения.
Итак, мы разобрали основные моменты, что такое отрезок, его свойства и как определяется длина отрезка. Далее разберем более подробно, как на практике происходит измерение длины отрезка и его сравнение с другими отрезками.
Измерение длины отрезка
Для измерения длины отрезков в геометрии используются специальные инструменты - линейки, циркули, штангенциркули и другие.
Процесс измерения отрезка линейкой выглядит следующим образом:
- Прикладываем линейку так, чтобы один из концов отрезка совпал с нулевым делением на линейке.
- Считаем, сколько раз единичный отрезок длины 1 см уложился в измеряемом отрезке.
- Если отрезок не укладывается целое число раз, используем доли единичного отрезка (миллиметры).
Циркуль позволяет откладывать и сравнивать отрезки, не прибегая к линейке. Для этого делают так:
- Устанавливают ножки циркуля на концы измеряемого отрезка.
- Переносят циркуль к началу другого отрезка, не меняя раствора ножек.
- Сравнивают, совпадает ли конец второго отрезка с раствором циркуля.
Сравнение отрезков
Длина отрезка окружности может быть найдена по формуле L = r * θ, где:
- L - длина дуги или радиуса окружности;
- r - радиус данной окружности;
- θ - центральный угол дуги в радианах.
Как же сравнить между собой два отрезка, чтобы определить, какой из них длиннее? Для этого используют два основных способа:
- Наложение отрезков друг на друга и визуальное сравнение.
- Измерение каждого отрезка выбранным инструментом с последующим числовым сравнением результатов.
Если в результате сравнения оказалось, что длины отрезков равны, то говорят, что отрезки равны.
Применение свойств отрезков
На практике знание свойств отрезков позволяет, например:
- Строить отрезок заданной длины по известным координатам его концов.
- Вычислять периметр многоугольника или окружности как сумму длин отрезков, образующих его контур.
В физике и других точных науках без знания длины отрезков не обойтись при расчетах и измерениях.
Задачи на длину отрезка
Длина отрезка часто фигурирует в различных геометрических задачах. Рассмотрим классический пример:
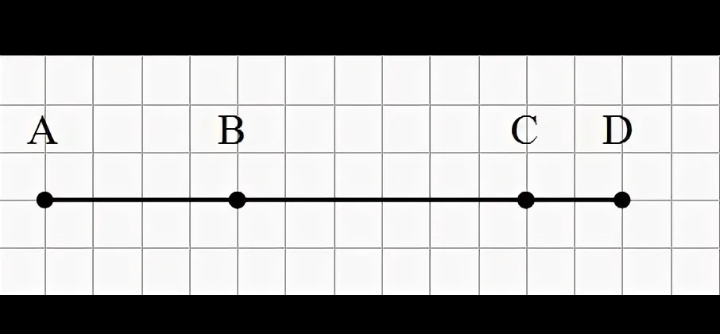
Здесь заданы длины трех отрезков: AB, BC и CD. Надо найти длину отрезка BD. Построим уравнение:
AB + BC + CD = BD + AB
4 см + 6 см + 2 см = BD + 4 см
BD = 4 см + 6 см + 2 см - 4 см = 8 см
Ответ: длина отрезка BD равна 8 см.
Формула длины отрезка
Как мы уже отмечали ранее, существует общая формула для вычисления длины произвольного отрезка:
L = n * l
где L - искомая длина отрезка, n - количество уложившихся в нем единичных отрезков, l - длина одного единичного отрезка.
Эта формула широко применяется на практике при решении задач на вычисление длин отрезков.
Интересные факты о длинах отрезков
- Самый длинный отрезок на Земле - экватор, его длина составляет 40 075 км.
- Диаметр Солнца - 1,39 миллиона км, это гигантский "отрезок".
- А самый маленький отрезок, который можно измерить на сегодня - порядка 0,0000001 мм.
Как видим, отрезки в природе могут варьироваться от нанометров до сотен миллионов километров!
Практические примеры
Давайте теперь рассмотрим несколько практических примеров применения знаний о длинах отрезков в реальной жизни.
Строительство и ремонт
При строительстве зданий, мостов, дорог и других сооружений очень важно точно вычислить необходимые длины отрезков. К примеру, при возведении многоэтажного дома надо рассчитать длины колонн, балок, перекрытий с точностью до сантиметра!
То же самое касается ремонтных и отделочных работ - будь то укладка плитки, покраска стен или замена труб. Знание длин помещений и конструктивных элементов критически важно для качественного результата.
Пошив и вязание одежды
Портные и дизайнеры одежды постоянно имеют дело с измерением длин - будь то рукава, воротники, юбки или брюки. От точности расчетов зависит, как в итоге будет сидеть готовое изделие.
То же самое касается вязания свитеров, носков и других вещей спицами или крючком - в прямом смысле слова приходится считать каждый отрезок нити!
Отрезки в искусстве
Даже в такой области как живопись, музыка или архитектура приходится иметь дело с отрезками и вычислением расстояний.
Художники используют линейки и циркули для построения правильной геометрии картины, соразмерности фигур. Архитекторы рассчитывают размеры зданий, пролетов мостов с точностью до миллиметра!
В музыке также встречаются отрезки - например, при обозначении длительностей нот или расстояний между ними на нотном стане.
Отрезки и вычислительная техника
Современные компьютеры также оперируют отрезками, в частности при работе графических редакторов. К примеру, при рисовании векторных изображений используются инструменты для создания и измерения отрезков.
Более того, в основе цифрового представления графики лежат дискретные отрезки пикселей. Из миллионов таких крохотных отрезков складывается любое цифровое изображение!



























