Отрезки - одно из фундаментальных понятий геометрии. Без знания того, что такое отрезки в геометрии , невозможно построение большинства геометрических фигур и доказательство многих теорем. Давайте разберемся подробно, что представляют собой отрезки, каково их определение и основные свойства.
Определение отрезка
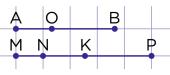
Что такое отрезок в геометрии? Определение звучит так: это часть прямой, ограниченная с двух сторон точками. Эти точки называются концами отрезка. Расстояние между концами отрезка называется его длиной.
Отрезок AB - это часть прямой AB, заключенная между точками A и B. Точки A и B называются концами отрезка, а расстояние между ними - длиной отрезка AB.
Отрезок обычно обозначается двумя заглавными буквами латинского алфавита. Например: AB, CD, MN.
Отличие отрезка от прямой и луча
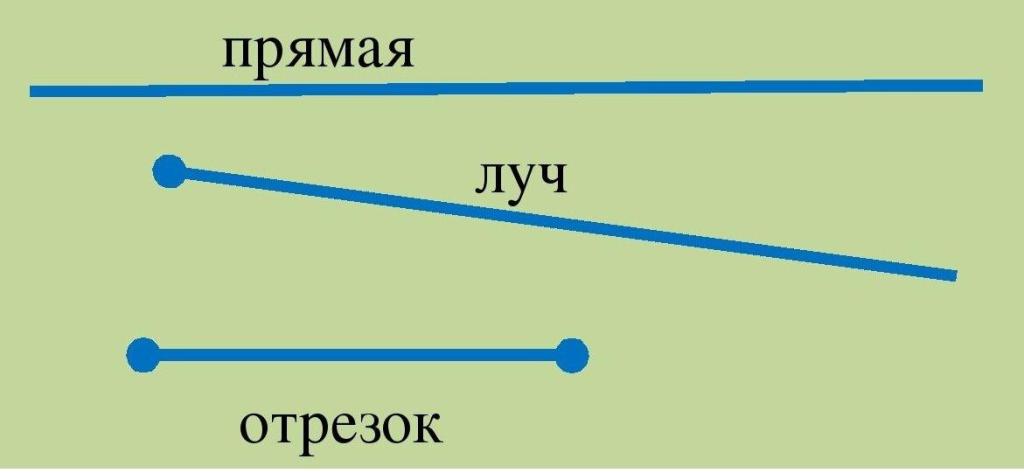
Часто возникает вопрос: чем отрезок отличается от прямой и луча?
- Прямая не имеет начала и конца, она бесконечна в обе стороны.
- Луч начинается в некоторой точке, но бесконечно протяжен в одну сторону.
- Отрезок ограничен с двух концов точками, то есть конечен.
Направленные и ненаправленные отрезки
Различают направленные и ненаправленные отрезки:
- Для ненаправленного отрезка неважно, в каком порядке записаны его концы, то есть AB = BA.
- У направленного отрезка или вектора порядок важен, поэтому AB и BA - это разные отрезки.
Основные свойства отрезков
Рассмотрим теперь основные свойства отрезков в геометрии.
Что такое равные отрезки в геометрии
Два отрезка называются равными, если они имеют одинаковую длину. Обозначается это так:
AB = CD (отрезки AB и CD равны)
Сумма двух отрезков
Если отрезки AB и BC имеют общую конечную точку B, то суммой этих отрезков называется отрезок AC:
AB + BC = AC
Деление отрезка пополам
Точка O называется серединой отрезка AB, если делит его пополам, то есть:
AO = OB
Через две точки A и B можно провести только один отрезок AB. Это одно из фундаментальных свойств отрезков в геометрии.
Параллельные и перпендикулярные отрезки
Два отрезка на плоскости могут располагаться параллельно или перпендикулярно:
- Параллельные отрезки - отрезки, которые лежат на параллельных прямых.
- Перпендикулярные отрезки - отрезки, концы которых соединены перпендикулярными прямыми.
Отрезок как элемент других фигур
Отрезки часто выступают в качестве элементов более сложных геометрических фигур:
- Стороны треугольника - это отрезки
- Диагонали и стороны четырехугольников - отрезки
- Ребра многогранников в пространстве - тоже отрезки
Системы отрезков
В геометрии рассматривают также системы отрезков - бесконечные последовательности отрезков с общими свойствами. Одним из важных свойств является сходимость отрезков к общей точке при сокращении их длины.
Отрезки в стереометрии
Понятие отрезка широко используется не только в планиметрии, но и в стереометрии - разделе геометрии, изучающем фигуры в пространстве.
Например, ребра многогранников представляют собой отрезки. Из отрезков можно составлять различные пространственные фигуры:
- Треугольная пирамида - четыре треугольника с общей вершиной
- Параллелепипед - шесть прямоугольников, в которых противоположные стороны попарно параллельны
При вычислении объемов многогранников используются отрезки в качестве исходных данных о ребрах фигур.