Гипербола - одна из основных кривых в геометрии. Она имеет интересную форму и широко используется в решении практических задач. Но многие считают ее построение сложным и затратным по времени.
Что такое гипербола и где она встречается
Итак, давайте разберемся, что же представляет собой гипербола. Гипербола – это график функции, заданной формулой y = k/x, где k ≠ 0.
Такая функция называется обратной пропорциональностью. График гиперболы симметричен относительно начала координат и состоит из двух ветвей, уходящих в бесконечность.
Гиперболы часто встречаются в реальной жизни. Например:
- Траектории движения космических тел под действием центростремительных и центробежных сил
- Движение частиц в ускорителях
- Оптические системы телескопов и микроскопов
- Графики спроса и предложения в экономике
Основные элементы и свойства гиперболы
Чтобы построить гиперболу, нужно знать ее основные элементы и свойства:
- Фокусы - две точки, обозначаемые F1 и F2
- Вершины - точки пересечения гиперболы с ее осью симметрии
- Полуоси - отрезки от центра до вершин
- Асимптоты - прямые, к которым стремятся ветви гиперболы
- Эксцентриситет - определяет "вытянутость" гиперболы
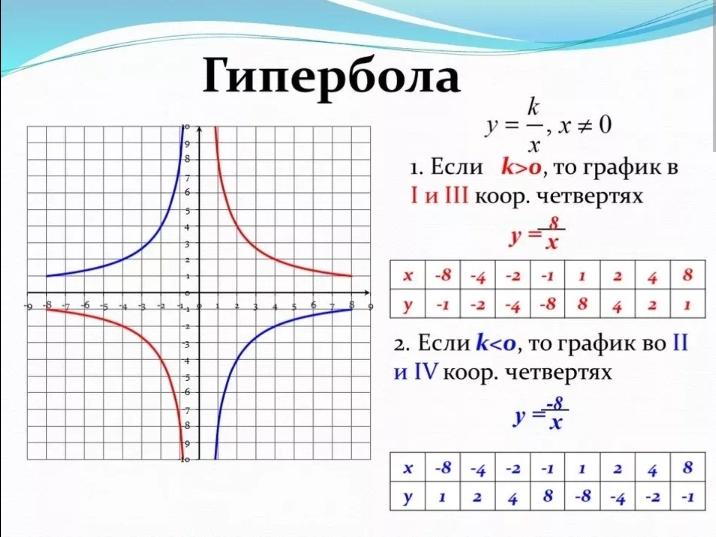
Кроме того, гипербола может располагаться в разных четвертях координатной плоскости в зависимости от знака коэффициента k.
| k > 0 | Гипербола в I и III четвертях |
| k < 0 | Гипербола во II и IV четвертях |
Чем больше k по модулю, тем дальше ветви гиперболы отстоят от начала координат.
Как построить гиперболу по уравнению
Допустим, у нас есть уравнение гиперболы в каноническом виде:
x2/a2 - y2/b2 = 1
Как по нему построить гиперболу?
- Задать координатные оси
- Отметить центр, вершины, фокусы
- Провести асимптоты
- Найти несколько точек гиперболы, подставив значения x и y в уравнение
- Соединить полученные точки плавной линией - это и есть гипербола
Давайте рассмотрим численный пример с пошаговым решением.
Пример пошагового построения гиперболы по уравнению
Рассмотрим построение гиперболы на примере:

Как построить гиперболу по функции
Если гипербола задана функцией вида y = k/x, построение тоже не вызовет затруднений. Действуем по алгоритму:
- Строим координатные оси
- Задаемся несколькими значениями x, вычисляем соответствующие значения y
- Наносим полученные точки на координатную плоскость
- Соединяем точки плавной линией, получаем график
Особенности построения гиперболы в различных четвертях
Как мы уже говорили, в зависимости от знака коэффициента k гипербола может располагаться в I и III или во II и IV четвертях координатной плоскости.
Это нужно учитывать при построении. Например, если k < 0, нам понадобится брать и положительные, и отрицательные значения x.
Полезные советы для более точного построения
Чтобы построить гиперболу быстро и аккуратно, придерживайтесь нескольких простых советов:
- Используйте координатную сетку в клетку
- Тщательно откладывайте значения x и y
- Пользуйтесь линейкой или циркулем для проведения плавных линий
- Делайте аккуратные пометки для каждой найденной точки
Если вы будете следовать этим рекомендациям, ваша гипербола получится ровной и точной.
Типичные ошибки при построении гиперболы
Самые распространенные ошибки, из-за которых гипербола может быть построена неправильно:
- Неверное определение четвертей
- Ошибки в вычислении координат точек
- Неаккуратное соединение точек
- Неправильный масштаб по осям
Чтобы их избежать, внимательно выполняйте все шаги построения и следите за деталями!
Построение гиперболы для функции y = 4/x
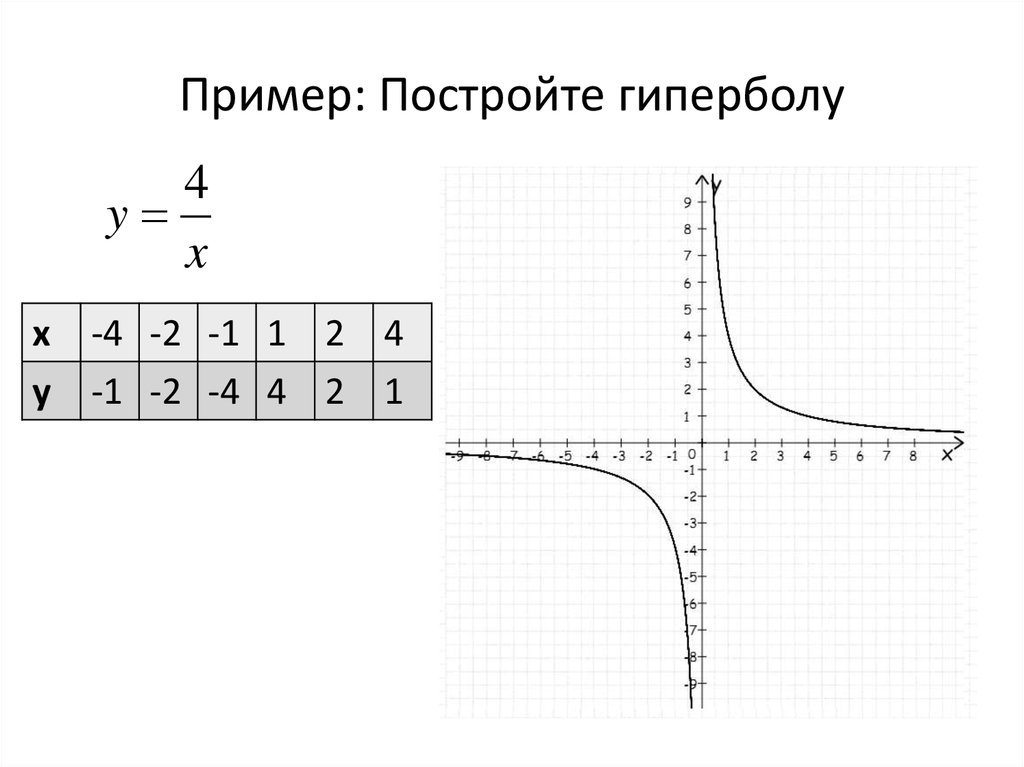
Для функции y = 4/x составим таблицу значений:
| x | -4 | -2 | -1 | 1 | 2 | 4 |
| y | -1 | -2 | -4 | 4 | 2 | 1 |
Отмечаем эти точки на координатной плоскости:
(-4; -1), (-2; -2), (-1; -4), (1; 4), (2; 2), (4; 1)
Соединяем точки плавными линиями - получаем гиперболу, расположенную симметрично относительно начала координат в 1-й и 3-й четвертях.
Построение гиперболы методом симметрии
Если гипербола симметрична, достаточно найти точки для одной ее половины, например правой ветви в 1-й четверти.
Затем отразить эти точки симметрично относительно оси OY - так получим точки для левой ветви в 3-й четверти.
Это позволяет сэкономить время на вычислениях и упрощает построение.
Построение гиперболы с помощью циркуля и линейки
Для более чистого и аккуратного построения гиперболы используйте следующие инструменты:
- линейку для проведения осей координат и асимптот;
- циркуль для откладывания отрезков заданной длины (полуосей, расстояний до фокусов);
- карандаш и ластик для нанесения и исправления точек.
Это позволит выполнить построение более аккуратно и избежать неточностей от руки.
Проверка правильности построенной гиперболы
Чтобы убедиться, что гипербола построена верно, необходимо:
- Проверить симметричность относительно начала координат
- Убедиться, что ветви уходят в бесконечность и не пересекают асимптот
- Подставить координаты какой-нибудь точки гиперболы в исходное уравнение или функцию
Если все условия выполняются - гипербола построена верно!

























