Длина дуги окружности - один из важнейших параметров при решении множества геометрических, инженерных и физических задач. От точности ее вычисления напрямую зависят результаты расчетов конструкций, построение чертежей, определение характеристик движения тел и многое другое. В этой статье мы подробно разберем основные определения, формулы и методы вычисления длины дуг окружности, а также приведем практические примеры и рекомендации.
Основные понятия и определения
Прежде чем перейти к формулам и методам расчета, давайте разберемся в терминологии и основных элементах дуги окружности. Дуга окружности - это часть окружности, заключенная между двумя ее точками и не содержащая точек самопересечения.
Основными элементами дуги окружности являются:
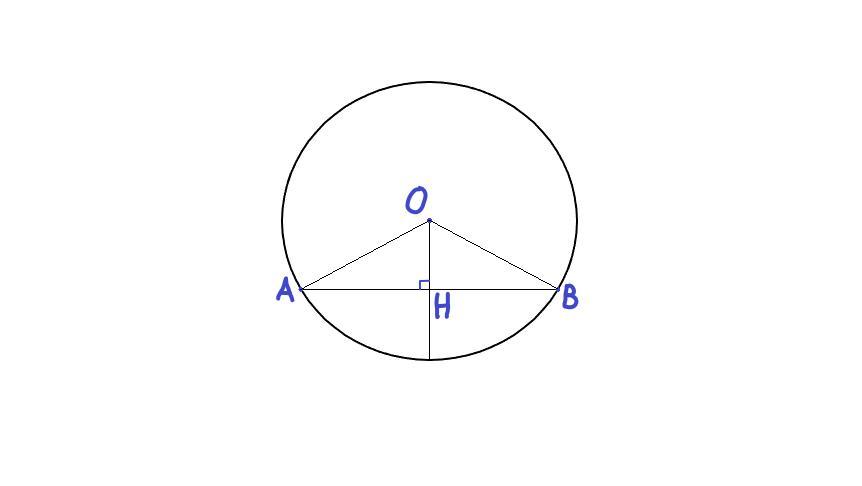
- Концы дуги - точки A и B
- Хорда AB - отрезок, соединяющий концы дуги
- Радиус-векторы OA и OB, проведенные из центра окружности O в концы дуги
- Центральный угол AOB, образованный радиусами OA и OB
Различают несколько основных видов дуг:
- Полная окружность - дуга с центральным углом 360° (2π радиан)
- Полуокружность - дуга с центральным углом 180° (π радиан)
- Сектор окружности - часть круга, ограниченная дугой и двумя радиусами
Дуги могут быть представлены в угловых единицах - градусах или радианах, по величине их центральных углов. При этом равные по углу дуги разных окружностей необязательно равны по длине. Их длины будут совпадать, только если радиусы окружностей одинаковы.
Если две точки A и B делят окружность пополам, образуя центральный угол 180°, то возникает две дополнительные дуги AB. Одна из них называется большей, а другая - меньшей полуокружностью.
Важно отличать длину дуги окружности от площади сектора, образованного этой дугой. Для вычислений используются разные формулы. Рассмотрим их подробнее.
Формула через радиус и угол
Наиболее часто используемая формула связывает длину дуги с радиусом окружности R и величиной центрального угла φ:
L = π R · φ / 180°
где L - длина дуги, R - радиус окружности, φ - центральный угол в градусах, π – константа, равная примерно 3,14.
Эта формула хорошо подходит в случае, когда известен радиус окружности и задан центральный угол дуги. Пример расчета длины дуги по этой формуле будет приведен ниже.
Формула через диаметр окружности
Также длину дуги можно выразить через диаметр окружности D. Для этого в формуле вместо радиуса R подставляем D/2:
L = π × d.
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Формула через площадь круга
Длина дуги окружности можно также найти, зная площадь S круга, к которому принадлежит дуга:
L = (2 : (4 × π))/S
Где S - площадь окружности, L - длина дуги, π – константа, равная примерно 3,14.
Формула Гюйгенса через хорду
Данная формула позволяет рассчитать приблизительную длину дуги через длину ее хорды AB и хорды АМ перпендикуляра, опущенного из середины хорды на дугу:
p≈2l+31(2l−L)
Для использования формулы Гюйгенса необходимо выполнить следующее геометрическое построение:
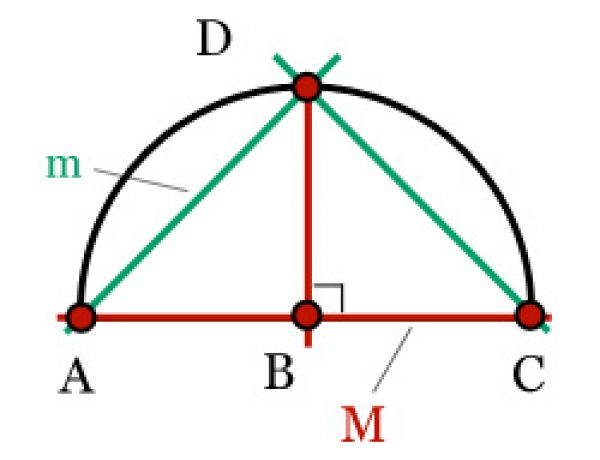
- Соединить концы дуги AB хордой
- Найти середину хорды M
- Из точки M опустить перпендикуляр CM на дугу
- Измерить длину хорды AB = L
- Измерить длину хорды АМ = l
Подставляя полученные значения L и l в формулу Гюйгенса, можно найти приблизительную длину исследуемой дуги.
Следует отметить, что формула Гюйгенса имеет некоторую погрешность, которая возрастает при увеличении центрального угла дуги. Поэтому ее рекомендуется использовать для небольших дуг в пределах 60°.
Далее рассмотрим конкретные численные примеры расчета длины дуг окружности различными методами.






















