Кварто-квинтовый круг, или просто квинтовый круг - это графическое представление взаимосвязей между всеми мажорными и минорными тональностями. Впервые он был описан в 1679 году в книге «Идея грамматики мусикийской» теоретиком Николаем Дилецким.
С тех пор квинтовый круг стал неотъемлемым инструментом музыкантов, композиторов и теоретиков. Он наглядно демонстрирует родство тональностей и помогает ориентироваться в сложных гармонических построениях.
Давайте разберемся, как устроен квинтовый круг и почему он так важен для понимания логики музыкального языка.
История создания квинтового круга тональностей
Квинтовый круг тональностей, или кварто-квинтовый круг, был впервые описан в 1679 году в книге «Идея грамматики мусикийской» композитора и теоретика музыки Николая Дилецкого. До этого музыканты использовали линейную систему тональностей, не отражавшую взаимосвязи между ними. Квинтовый круг позволил наглядно представить родство тональностей, основанное на квинтовом и квартовом кругообороте.
Систематизация тональностей в виде квинтового круга сыграла важную роль в развитии гармонии и полифонии. В частности, И.С. Бах использовал квинтовый круг при сочинении «Хорошо темперированного клавира» - цикла прелюдий и фуг во всех мажорных и минорных тональностях, демонстрируя равноправие тональностей.
Таким образом, благодаря описанию квинтового круга Николаем Дилецким и его последующему применению ведущими композиторами произошла гармонизация ладовой системы, ставшая фундаментом европейской академической музыки.
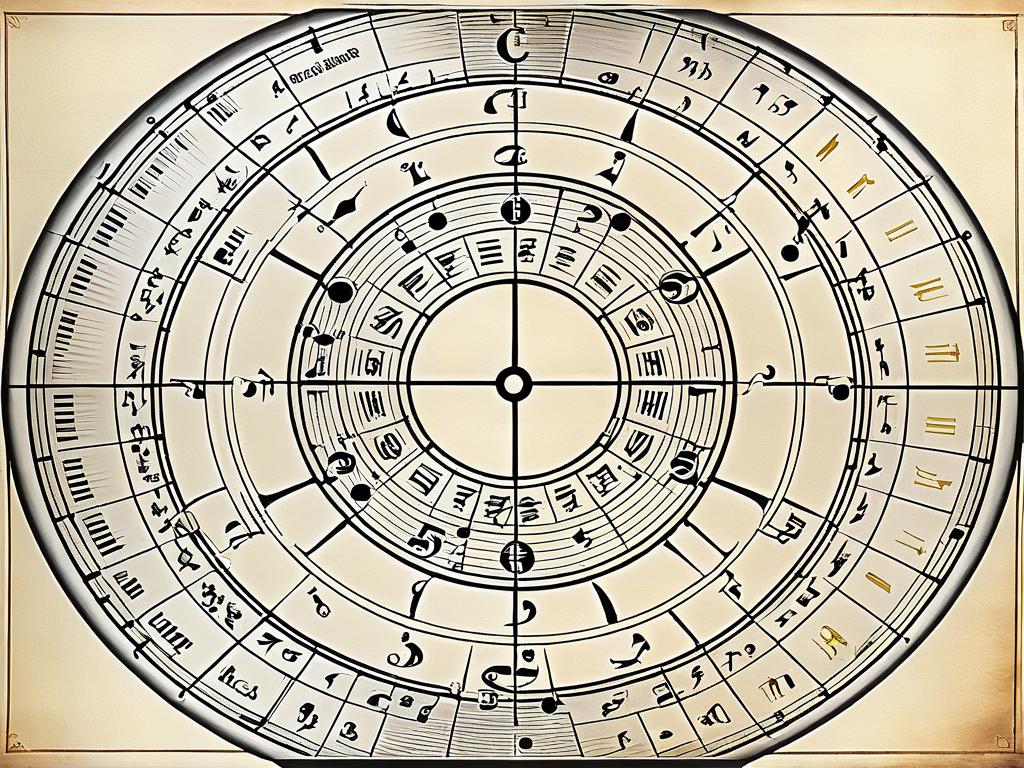
Принцип устройства кварто-квинтового круга
Квинтовый круг строится на основе чистых квинт и кварт — интервалов, соответственно, в 7 и 5 ступеней по частоте звука. Квинтовый круг состоит из 12 звуковых классов, соответствующих 12 нотам равномерно темперированного строя.
В центре квинтового круга расположена нота «до», от которой последовательным прибавлением квинт (или вычитанием кварт) получают остальные ноты. Так, при движении по часовой стрелке через каждую квинту добавляется по одному диезу, а против часовой — по одному бемолю в тональности.
Так как в октаве 12 полутонов, то сделав полный круг в 12 квинт, мы вернемся к исходной ноте. Однако на практике используют не более 6 квинт в каждую сторону, чтобы избежать тональностей с большим количеством знаков.
Также в квинтовом круге принято располагать мажорные тональности снаружи, а родственные им минорные — внутри. Это позволяет наглядно показывать параллельные тональности и их ключевые знаки.
Практическое применение квинтового круга
Квинтовый круг широко используется в музыкальной педагогике и практике. Он помогает определить тональности, родственные заданной, что важно при модуляции — переходе из одной тональности в другую.
Также квинтовый круг применяется для:
- визуализации аккордов в конкретной тональности и их функциональной принадлежности;
- подбора аккомпанемента и импровизации;
- анализа музыкальных произведений с точки зрения ладотонального плана и модуляций.
Композиторы используют квинтовый круг в процессе сочинения музыки, чтобы выбирать тональности и планировать модуляции. Например, чтобы плавно перейти из Си-бемоль мажора в Ми мажор, можно использовать три промежуточные тональности по квинтовому кругу.
Таким образом, квинтовый круг является универсальным инструментом музыканта при работе с ладотональным материалом — как в творчестве, так и в педагогике.
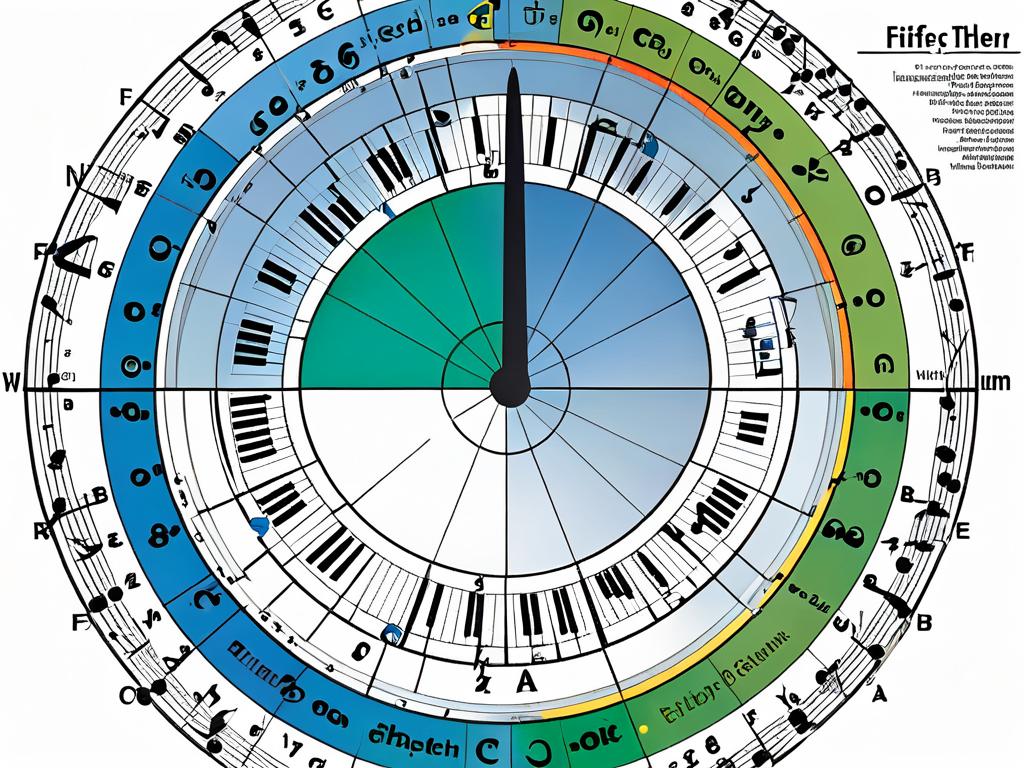
Значение квинтового круга для музыкального анализа и композиции
Квинтовый круг является мощным аналитическим инструментом, позволяющим глубже понять структуру музыкального произведения. Анализируя ладотональный план с точки зрения квинтового круга, можно выявить особенности модуляций, тональное родство фрагментов и тем, роль тональностей в драматургии.
Также квинтовый круг применяется при анализе гармонии. Он дает представление о функциональной принадлежности аккордов конкретной тональности, помогает определить разрешение неустойчивых гармоний.
В композиторской практике квинтовый круг используется на этапе планирования формы будущего произведения. Композитор выбирает основные тональности с учетом их драматургической роли и намечает возможные пути модуляций между ними по квинтовому кругу.
Перспективы применения кварто-квинтового круга
Несмотря на многовековую историю, квинтовый круг не утратил актуальности и в наши дни. Перспективным направлением является создание интерактивных онлайн-приложений для изучения квинтового круга, возможностей генерации гармонических последовательностей в заданной тональности.
Также актуально расширенное применение квинтового круга в джазе и популярных стилях. В частности, гармонические схемы джазовых стандартов можно анализировать с точки зрения квинтового круга, что дает интересные результаты.
Перспективным является сравнительный анализ европейского мажоро-минора и традиционных ладовых систем Востока, Индии для выявления универсальных закономерностей в восприятии и организации музыкального материала разных культур.























