Существует множество разновидностей головоломок, предназначенных для тренировки ума и развития логического мышления. Некоторые из них настолько сложны, что над их решением бьются даже опытные профессионалы. В этой статье мы рассмотрим самые известные примеры таких загадок.
Будут разобраны различные типы головоломок: судоку, логические задачи, проблемы узнавания и другие. Для каждой категории приведен конкретный пример наиболее трудной в мире задачи с объяснением, что делает ее столь сложной. Цель статьи - не только перечислить самые непостижимые головоломки, но и разобрать принципы их работы, раскрыть особенности, которые заставляют "убиваться" над ними даже опытных решателей.
Самая трудная в мире судоку
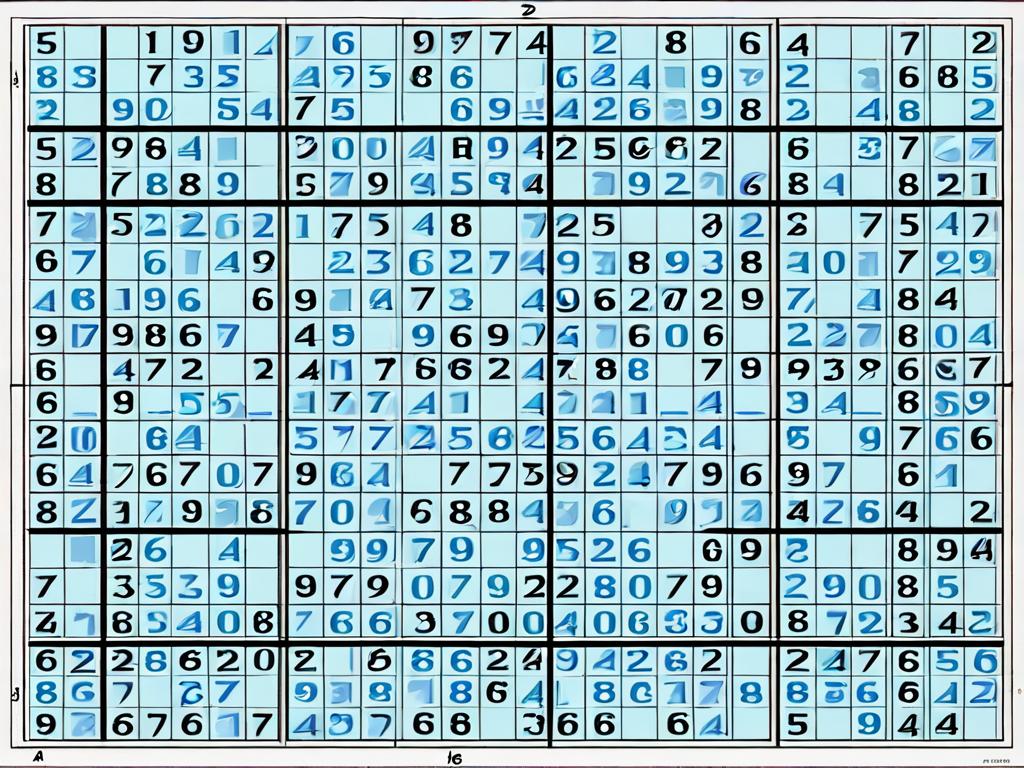
Судоку - это числовая головоломка японского происхождения. Цель состоит в заполнении свободных клеток цифрами от 1 до 9 так, чтобы в каждой строке, в каждом столбце и в каждом малом квадрате 3х3 каждая цифра встречалась только один раз. В 2012 году финский математик Арто Инкала разработал «самую сложную в мире судоку», которую оценил в 11 баллов из 5 по шкале сложности.
Эта судоку действительно крайне сложная. Чтобы ее решить, нужно проявить необычайную изобретательность и настойчивость. Но именно в преодолении трудностей и заключается особая притягательность подобных головоломок. Их решение - это настоящая тренировка ума, развитие логического и абстрактного мышления.
Так что самая сложная в мире - это отличный вызов для любителей интеллектуальных игр и головоломок. Попробовать решить ее - значит испытать свои умственные способности в необычных условиях. А разгадав ее, можно по праву гордиться своим достижением.
«Проблема трех богов» - вершина логических головоломок
Одной из самых известных логических головоломок является «Проблема трех богов», придуманная американским философом Джорджем Булосом. Суть ее заключается в следующем:
- Есть три бога - А, B и C. Один из них всегда говорит правду, другой всегда лжет, а третий отвечает случайным образом.
- Необходимо определить, кто есть кто, задав каждому богу по одному вопросу с ответом «да» или «нет».
- Ответы богов «da» и «ja», но неизвестно, какой означает «да», а какой «нет».
Решение этой головоломки требует нестандартного подхода и тонкой логики. Нужно тщательно продумать формулировки вопросов, чтобы однозначно определить роль каждого бога. Эта задача на грани абсурда заставляет по-новому взглянуть на возможности человеческого разума.
«Проблема трех богов» по праву считается одной из самых сложных логических головоломок в мире. Ее решение - настоящее испытание интеллекта и доказательство неординарности мышления.
Задачи распознавания образов Бонгарда
Одним из самых нестандартных типов головоломок являются задачи распознавания образов, разработанные выдающимся советским ученым Михаилом Бонгардом в 60-х годах прошлого века. Суть этих задач заключается в следующем: даются две группы изображений. Нужно найти правило, по которому подобраны все картинки в левой группе, но которому не соответствует ни одна картинка в правой группе.
Решение задач Бонгарда требует нестандартного творческого мышления и способности распознавать скрытые закономерности. Здесь нет готовых алгоритмов, каждая задача - уникальная головоломка. Это настоящее испытание интеллекта. Некоторые примеры задач Бонгарда по праву считаются самыми сложными головоломками в мире. Их решение требует невероятной изобретательности, концентрации и упорства. Это путешествие в самые неожиданные уголки человеческого разума.

Хитроумные задачи Мартина Гарднера
Американский математик Мартин Гарднер прославился как автор множества оригинальных головоломок, требующих нестандартного подхода. Одна из его самых интересных задач - найти число, для которого требуется минимальное количество шагов, чтобы свести его к одной цифре путем перемножения цифр. Гарднер назвал это «числом стойкости».
Например, для числа 77 потребуется 4 шага: 77 -> 49 -> 36 -> 18 -> 8. Таким образом, числу 77 соответствует «число стойкости» 4. Задача кажется простой, но требует тщательного перебора вариантов. Это отличный пример того, как Гарднер умел превращать математические казусы в увлекательные интеллектуальные головоломки. Многие задачи Гарднера в свое время считались самыми сложными в мире. Они и сегодня остаются вершиной остроумия и изобретательности в области математических головоломок.
























