Параллельность плоскостей: условие и свойства

Параллельность плоскостей является понятием, впервые появившимся в эвклидовой геометрии более двух тысяч лет назад.

Основные характеристики классической геометрии

Рождение этой научной дисциплины связано с известнейшим трудом древнегреческого мыслителя Эвклида, написавшего в третьем веке до нашей эры памфлет «Начала». Разделенные на тринадцать книг, «Начала» являлись высшим достижением всей античной математики и излагали фундаментальные постулаты, связанные со свойствами плоских фигур.

Классическое условие параллельности плоскостей было сформулировано следующим образом: две плоскости могут назваться параллельными, если они между собой не имеют общих точек. Об этом гласил пятый постулат эвклидового труда.

Свойства параллельных плоскостей

В эвклидовой геометрии их выделяют, как правило, пять:

• Свойство первое (описывает параллельность плоскостей и их единственность). Через одну точку, которая лежит вне конкретной данной плоскости, мы можем провести одну и только одну параллельную ей плоскость

• Свойство второе (также имеет название свойства трех параллельностей). В том случае, когда две плоскости являются параллельными по отношению к третьей, между собой они также параллельны.
  

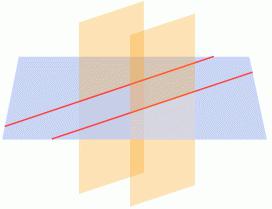
• Свойство третье (иными словами оно называется свойством прямой, пересекающей параллельность плоскостей). Если отдельно взятая прямая линия пересекает одну из этих параллельных плоскостей, то она пересечет и другую.

• Свойство четвертое (свойство прямых линий, высеченных на плоскостях, параллельных друг другу). Когда две параллельные плоскости пересекаются третьей (под любым углом), линии их пересечения также являются параллельными

• Свойство пятое (свойство, описывающее отрезки разных параллельных прямых, которые заключены между плоскостями, параллельными друг другу). Отрезки тех параллельных прямых, которые заключены между двумя параллельными плоскостями, обязательно равны.

Параллельность плоскостей в неэвклидовых геометриях

Такими подходами являются в частности геометрия Лобачевского и Римана. Если геометрия Эвклида реализовывалась на плоских пространствах, то у Лобачевского в отрицательно искривленных пространствах (выгнутых попросту говоря), а у Римана она обретает свою реализацию в положительно искривленных пространствах (иными словами – сферах). Существует весьма распространенное стереотипное мнение, что у Лобачевского параллельные плоскости (и линии тоже) пересекаются.

Однако это неверно. Действительно рождение гиперболической геометрии было связано с доказательством пятого постулата Эвклида и изменением взглядов на него, однако само определение параллельных плоскостей и прямых подразумевает, что они не могут пересечься ни у Лобачевского, ни у Римана, в каких бы пространствах они ни реализовывались. А изменение взглядов и формулировок заключалось в следующем. На смену постулату о том, что лишь одну параллельную плоскость можно провести через точку, не лежащую на данной плоскости, пришла другая формулировка: через точку, которая не лежит на данной конкретной плоскости, могут проходить две, по крайней мере, прямые, которые лежат в одной плоскости с данной и не пересекают ее.