Современную цивилизацию попросту невозможно себе представить без чисел. Мы сталкиваемся с ними каждый день, производим над ними десятки, сотни и тысячи действий при помощи компьютеров. Мы так к этому привыкли, что история развития чисел нас совершенно не интересует, а многие об этом попросту никогда и не задумывались. Но без знания прошлого никогда нельзя понять настоящее, а потому всегда следует стремиться к постижению истоков.

Развитие
В математике нет компонента важнее. Несмотря на это, число как понятие развивалось на протяжении не одной тысячи лет, пока ученые умы всего мира не договорились-таки о том, как воспринимать его.
Первые прикладные дисциплины, которые настоятельно требовали появления этого понятия, были связаны с земледелием, строительством и наблюдениями за звездами. В свою очередь, изучение звездного неба и классификация всех измерений были жизненно необходимы для развития судоходства и международной торговли, без которой не могло развиваться ни одно государство.
Немного философии
Даже самые примитивные цифры вырабатывались и приводились к единому виду на протяжении многих веков. Многие из них образовались в результате творческого переосмысления слов или отдельных букв. Знаменитый Пифагор говорил, что цифры являются тем таинственным, эфемерным веществом, из которого образована вся Вселенная. В общем-то, согласно современным представлениям науки, он был во многом прав.
Китайцы делили числа на две большие категории (которые сохранились и по сей день):
- Нечетные, или Ян. В древнекитайской философии они символизировали небо и благоприятность.
- Соответственно, четные (Инь). Это понятие символизировало землю и нестабильность.
С древнейших времен…

Антропологи и археологи точно установили, что человек умел считать уже в каменном веке. Поначалу первые числа обозначались исключительно количеством пальцев на руках и ногах. Использовали их для подсчета шагов, добычи, врагов... Сперва человек нуждался лишь в нескольких простых числах, но развитие общества требовало все большего усложнения системы. Это не только привело к развитию зачатков математики, но и способствовало развитию всей человеческой цивилизации в общем, так как счет требовал напряженного интеллектуального труда.
Так что история возникновения и развитие числа неразрывно связаны с улучшением разума и стремлением наших далеких предков к самосовершенствованию. Чем чаще они смотрели на звезды, тем сильнее задумывались о математических закономерностях (пусть даже на примитивном уровне) в окружающем их мире, тем мудрее становились.
Интуитивное понятие о числе
Как только произошел первый бартер, человек начал учиться сравнивать количество одних предметов с аналогичными значениями для предлагаемых ему товаров. Появились понятия «больше», «меньше», «равно», «столько же». Знания быстро усложнялись, а потому вскоре появилась необходимость в системе счета.

Числа же, которыми описываются свойства этих самых предметов, существуют, но потрогать или сравнить их было нельзя. Это свойство приводило людей в трепет, они приписывали числам магические, сверхъестественные качества.
Некоторые доказательства гипотез
Ученые давно предполагали, что изначально люди использовали только три понятия: «один», «два» и «много». Данная гипотеза блестяще подтверждается тем фактом, что во многих древних языках существует именно три формы (в древнегреческом, к примеру): единственного, двойственного и множественного числа. Чуть позже человек научился отличать, к примеру, двух бизонов от трех. Изначально счет был связан с каким-то определенным набором предметов.
Вплоть до недавнего времени у коренных австралийцев и полинезийцев было только два числительных: «один» и «два», а все прочие числа люди получали, комбинируя их. К примеру, число три – это два и один, четыре – два и два. Это удивительно напоминает двоичную систему исчисления, которую сейчас использует вычислительная техника! Впрочем, суровая жизнь тех времен заставляла учиться, а потому примитивный счет быстро превратился в математическую науку.
Вавилон и Месопотамия
В древнем Вавилоне математики развернулись особенно широко, так как в этом государстве создавались исполинские, чрезвычайно сложные сооружения, которые без вычислений было невозможно возвести. Как ни странно, но вавилоняне не питали к числам особенного трепета, так что история развития понятия числа в широком понимании этого слова началась именно с них.
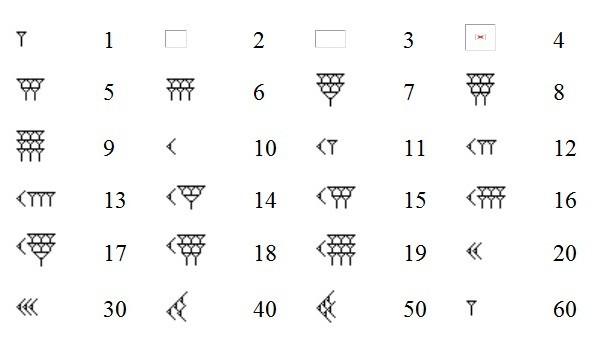
Кроме того, их система исчисления зиждилась на шестидесятеричном способе измерения, который вавилоняне, как предполагают ученые, позаимствовали у шумерской цивилизации. Не стоит думать, будто бы в этой области история развития понятия числа остановилась. Мы до сих пор используем понятие 60 минут, 60 секунд, 360 градусов в контексте измерения окружности.
Предвосхитившие Пифагора
Древние писцы в Вавилоне уже неплохо знали свойства прямоугольных треугольников. Кроме того, ими выполнялось исчисление объёма усечённой пирамиды. Сегодня точно известно, что история развития рациональных чисел берет свое начало именно с тех времен: математики Месопотамии и Вавилона не только активно использовали дроби, но даже могли решать с их помощью задачи, включающие до трех неизвестных значений!
В недавнем прошлом современные математики с удивлением узнали, что их древние предшественники преуспели в извлечении не только квадратного, но даже кубического корня. Они также вплотную подошли к определению числа Пи, грубо округляя его до трех. Следует отметить, что египтяне впоследствии сумели куда более точно вычислить его значение (3,16).
Натуральные числа
Не менее древней является история развития натурального числа. В настоящее время считается, что первым этот термин использовал в своих трудах древнеримский ученый Боэций (480-524 гг.), но еще задолго до него Никомах из Геразы писал в своих трудах о натуральном, природном ряде чисел.

С их появлением был сделан важнейший шаг к возникновению математики и алгебры в том виде, в котором мы их знаем сегодня. Современные математики с уверенностью говорят о бесконечности ряда натуральных чисел. Конечно же, в древности человек об этом не знал. Количество, которое люди попросту не могли себе вообразить, обозначалось словами «тьма», «легион», «множество» и так далее. Так что история развития линии числа является чрезвычайно древней…
Теория множества
Сперва натуральный ряд чисел был крайне коротким. Но знаменитому Архимеду (III в. до н. э.) удалось значительно расширить данное понятие. Именно этот легендарный ученый написал труд «Псаммит», который его современники чаще называли так: «Исчисление песчинок». Он точно подсчитал количество крохотных частичек, которые теоретически могли занять весь объем шара диаметром 15.000.000.000.000 километров.
До Архимеда греки успели дойти до числа 10.000.000 мириад. Мириадой, впрочем, они называли количество в 10 000. Само это название происходит от греческого «мирос», что в переводе на русский означает «неизмеримо большое», «невероятно огромное». Архимед же пошел дальше: он начал использовать в своих расчетах понятие «мириада мириад», что впоследствии привело его к созданию собственной, авторской системы исчисления.
Максимальное значение, которое смог описать ученый, содержит 80.000.000.000.000.000 нулей. Если напечатать это число на длинной бумажной ленте, то ей можно опоясать весь земной шар по экватору более двух миллионов раз.
Таким образом, у всех натуральных чисел есть две важнейшие функции:
- Ими можно охарактеризовать количество любых предметов.
- С их помощью описываются признаки предметов в числовом ряду.
Действительные числа

Если вы внимательно читали статью, то могли догадаться о том, что история развития действительных чисел начинается с самой зари человечества. Поскольку понятие нуля было впервые (более-менее достоверные сведения) сформулировано в 876 году от Рождества Христова и введено в Индии, можно отметить эту дату как промежуточную.
Что же касается отрицательных значений, то впервые их описал Диофант (Греция) в третьем веке нашей эры, но «узаконены» они были только в Индии, практически одновременно с понятием «ноль».
Следует помнить, что история развития чисел в математике предполагала их существование еще в Древнем Египте, так как в результате вычислений они проявлялись нередко. Вот только в то время их считали «невозможными» и «нереальными», хотя изредка использовали в качестве промежуточных значений.
Рациональные числа
Вспомним, что рациональным числом называется дробь. В виде числителя в ней используется целое число, а знаменателем выступает число натуральное. Мы уже никогда не узнаем, когда и где это понятие возникло впервые, но им активно пользовались уже шумеры за несколько тысяч лет до нашей эры. Их примеру последовали греки и египтяне.
Комплексные числа
А вот их получили сравнительно недавно, сразу после выявления способов вычисления корней кубического уравнения. Сделал это итальянец Никколо Фонтана Тарталья (1499-1557 гг.) приблизительно в начале шестнадцатого века. И вот тогда он выяснил, что для решения разного рода задач далеко не всегда получается использовать только действительные числа.

Другая теория
Некоторые исследователи говорят, что впервые мнимые величины были упомянуты еще в 1545 году. Произошло это на страницах известного в ту пору труда «Великое искусство, или Об алгебраических правилах», который написал Джероламо Кардано. Тогда он пытался найти решение задачи о двух числах, которые при умножении дают 10, а при перемножении их значение возрастает до 40.
Долгое время перед математиками стоял вопрос о том, может ли быть их множество полностью замкнутым. Поясним: всегда ли операции над комплексными значениями приводят к получению комплексных же, вещественных результатов или дальнейшие изыскания могут привести к открытию чего-то совершенно нового? Впрочем, решение этой задачи находится в работах Абрахама де Муавра (они относятся еще к 1707 году), а также в трудах Роджера Котса, которые были опубликованы в 1722 году.
Вот и вся история развития числа. Кратко, конечно же, но статья все же рассматривает основные вехи исследований в этой области.


























