Теплоемкость газа - это количество энергии, которое поглощает тело при его нагревании на один градус. Проанализируем основные характеристики данной физической величины.

Определения
Удельная теплоемкость газа представляет собой величины единицы массы конкретного вещества. Ее единицами измерения являются Дж/(кг·К). Количество теплоты, которое поглощается телом в процессе изменения его агрегатного состояния, связано не только с начальным и конечным состоянием, но и со способом перехода.

Подразделение
Теплоемкость газов делят на величину, определяемую при неизменном объеме (Cv), постоянном давлении (Ср).
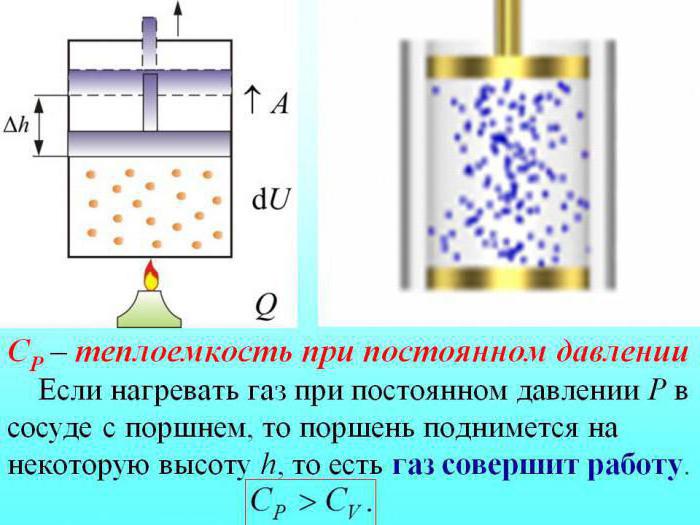
В случае нагревания без изменения давления некоторое количество тепла расходуется на производство работы расширения газа, а часть энергии затрачивается для увеличения внутренней энергии.
Теплоемкость газов при постоянном давлении определяется количеством теплоты, которое расходуется на повышение внутренней энергии.
Газообразное состояние: особенности, описание
Теплоемкость идеального газа определяется с учетом того, что Сp-Сv=R. Последнюю величину называют универсальной газовой постоянной. Ее величина соответствует 8,314 Дж/(моль·К).
При проведении теоретических вычислений теплоемкости, например описания связи с температурой, недостаточно пользоваться только термодинамическими методами, важно вооружиться элементами статической физики.
Теплоемкость газов предполагает вычисление среднего значения энергии поступательного движения некоторых молекул. Такое движение суммируется из вращательного и поступательного движения молекулы, а также из внутренних колебаний атомов.
В статической физике есть информация о том, что на каждую степень свободы вращательного и поступательного движения приходится для газа величина, которая равна половине универсальной газовой постоянной.

Интересные факты
У частицы одноатомного газа предполагается три поступательных степени свободы, поэтому удельная теплоемкость газа имеет три поступательные, две вращательные, одну колебательную степени свободы. Закон их равномерного распределения приводит к приравниванию удельной теплоемкости при неизменном объеме к R.
В ходе экспериментов было установлено, что теплоемкость двухатомного газа соответствует величине R. Подобное несоответствие теории с практикой объясняется тем, что теплоемкость идеального газа связана с квантовыми эффектами, поэтому при проведении расчетов важно использовать статистику, базирующуюся на квантовой механике.
Исходя из основ квантовой механики, любая система частиц, которые совершают колебания либо вращения, включая молекулы газа, обладает только некоторыми дискретными значениями энергии.
Если энергии теплового движения будет в системе недостаточно для возбуждения колебаний определенной частоты, подобные движения не вносят своего вклада в суммарную теплоемкость системы.
В итоге конкретная степень свободы становится «замороженной», к ней невозможно применить закон равнораспределения.
Теплоемкость газов – важная характеристика состояния, от которой зависит функционирование всей термодинамической системы.
Температура, при достижении которой закон равнораспределения можно будет применить к колебательной либо вращательной степени свободы, характеризуется квантовой теорией, связывает постоянную Планка с константой Больцмана.

Двухатомные газы
Промежутки между вращательными энергетическими уровнями таких газов составляют незначительное количество градусов. Исключение составляет водород, в котором значение температуры определяется сотнями градусов.
Именно поэтому теплоемкость газа при постоянном давлении сложно описать законом равномерного распределения. В квантовой статистике при определении теплоемкости учитывают, что ее колебательная часть в случае понижения температуры быстро снижается, достигает нулевого значения.
Подобное явление объясняет тот факт, что при комнатных температурах практически нет колебательной части теплоемкости, для двухатомного газа она соответствует постоянной R.
Теплоемкость газа при постоянном объеме в случае низких температурных показателей определяется с помощью квантовой статистики. Существует принцип Нернста, который называют третьим началом термодинамики. Исходя из его формулировки, молярная теплоемкость газа будет убывать при понижении температуры, стремиться к нулевому показателю.

Особенности твердых тел
Если теплоемкость смеси газов можно объяснить с помощью квантовой статистики, то для твердого агрегатного состояния тепловое движение характеризуется незначительными колебаниями частиц вблизи положения равновесия.
У каждого атома есть три колебательные степени свободы, поэтому в соответствии с законом равнораспределения молярную теплоемкость твердого тела можно рассчитать как 3nR, причем n – количество атомов в молекуле.
На практике подобное число является тем пределом, к которому стремится при высоких температурных показателях величина теплоемкости твердого тела.
Максимум можно получить при обычных температурах у некоторых элементов, включая металлы. При n=1 выполняется закон Дюлонга и Пти, а вот для сложных веществ достичь такого предела достаточно сложно. Поскольку в реальности предел невозможно получить, происходит разложение либо плавление твердого вещества.
История квантовой теории
Основателями квантовой теории считаются Эйнштейн и Дебай в начале двадцатого века. Она базируется на квантовании колебательных движений атомов в определенном кристалле. В случае невысоких температурных показателей теплоемкость твердого тела оказывается в прямо пропорциональной зависимости от абсолютной величины, взятой в кубе. Эта зависимость была названа законом Дебая. В качестве критерия, который позволяет отличать низкие и высокие температурные показатели, берется их сравнение с дебаевской температурой.
Определяется такая величина спектром колебаний атома в теле, поэтому серьезно зависит от особенностей его кристаллической структуры.
QD – это величина, которая имеет несколько сотен К, но, к примеру, у алмаза она существенно выше.
В величину теплоемкости металлов значительный вклад вносят электроны проводимости. Для ее вычисления используют квантовую статистику Ферми. Электронная проводимость для атомов металлов прямо пропорциональна абсолютной температуре. Поскольку она является незначительной величиной, она учитывается только при значениях температуры, стремящихся к абсолютному нулю.
Способы определения теплоемкости
В качестве основного экспериментального метода выступает калориметрия. Для проведения теоретического расчета теплоемкости используется статистическая термодинамика. Он допустим для идеального газа, а также для кристаллических тел, проводится на основе экспериментальных данных о строении вещества.
Эмпирические методики расчета теплоемкости идеального газа базируются на представлении о химическом строении, вкладе отдельных групп атомов в Ср.
Для жидкостей также применяют методы, которые основываются на применении термодинамических циклов, которые позволяют переходить от теплоемкости идеального газа к жидкости через производную температуры энтальпии процесса испарения.
В случае раствора расчет теплоемкости в качестве аддитивной функции не допускается, так как избыточная величина теплоемкости раствора в основном существенна.
Чтобы провести ее оценку, потребуется молекулярно-статистическая теория растворов. Самым сложным считается выявление теплоемкости гетерогенных систем в термодинамическом анализе.

Заключение
Изучение теплоемкости позволяет проводить расчеты энергетического баланса процессов, протекающих в химических реакторах, а также в иных аппаратах химического производства. Кроме того, эта величина необходима для подбора оптимальных видов теплоносителей.
В настоящее время осуществляется экспериментальное определение теплоемкости веществ для различных температурных интервалов – от низких значений до высоких величин – основной вариант определения термодинамических характеристик вещества. При проведении вычислений энтропии и энтальпии вещества применяют интегралы теплоемкости. Информация о теплоемкости химических реагентов в определенном температурном интервале позволяет рассчитывать тепловой эффект процесса. Информация о теплоемкости растворов позволяет рассчитывать их термодинамические параметры при любых температурных значениях в рамках анализируемого промежутка.
К примеру, для жидкости характерно расходование части тепла на изменение величины потенциальной энергии реагирующих молекул. Такую величину называют «конфигурационной» теплоемкостью, используют для описания растворов.
Сложно вести полноценные математические вычисления без учета термодинамических характеристик вещества, его агрегатного состояния. Именно поэтому для жидкостей, газов, твердых веществ используют такую характеристику как удельная теплоемкость, позволяющую характеризовать энергетические параметры вещества.


























