Определение и величина числа Грэма

При слове “бесконечность” у каждого человека возникают свои ассоциации. Многие рисуют в своем воображении море, уходящее за горизонт, а у других перед глазами появляется картина бескрайнего звездного неба. Совсем по-иному представляют себе бесконечность математики, привыкшие оперировать числами. Они уже много веков пытаются найти наибольшее, из требующихся для измерения физических величин. Одним из них является число Грэма. Сколько нулей в нем и для чего оно используется, расскажет эта статья.

Бесконечно большое число

В математике так называют такую переменную величину x_n, если для любого наперед заданного положительного числа M можно указать натуральное N такое, что для всех номеров n, больших N, верно неравенство |x_n| > M. Однако ни одно, например, целое число Z нельзя считать бесконечно большим, так как оно всегда будет меньше величины (Z + 1).

Несколько слов о "гигантах"

Самыми большими числами, имеющими физический смысл, принято считать:

• 10⁸⁰. Это число, которое принято называть квинквавигинтиллионом, принято для обозначения примерного количества кварков и лептонов (мельчайших частиц) Вселенной.
• 1 Гугол. Такое число в десятичной системе исчисления записывается как единица со 100 нулями. Согласно некоторым математическим моделям, со времени большого взрыва, до взрыва массивнейшей черной дыры должно пройти от 1 до 1,5 гугола лет, после чего наша вселенная перейдет в последнюю стадию своего существования, т. е. можно считать, что это число имеет некий физический смысл.
• 8,5 х 10¹⁸⁵. Постоянная Планка равна 1,616199 x 10^-35 м, т. е. в десятичной записи выглядит как 0,00000000000000000000000000000616199 м. В 1 куб. дюйме насчитывается около 1 гугола планковских длин. Подсчитано, что во всей нашей Вселенной может поместиться около 8,5 х 10¹⁸⁵ планковских длин.
• 2^{77 232 917} – 1. Это самое большое из известных простых чисел. Если его двоичная запись имеет довольно компактный вид, то для того, чтобы изобразить его в десятичной форме потребуется ни много ни мало - 13 миллионов знаков. Оно было найдено в 2017-м году в рамках проекта по поиску чисел Мерсенна. Если энтузиасты будут продолжать работать в этом направлении, то при нынешнем уровне развития вычислительной техники, в ближайшее время они вряд ли смогут найти число Мерсенна на порядок большее, чем 2^{77 232 917} – 1, хотя такой счастливчик получит 150 000 $ США.
• Гугоплекс. Тут все просто берем 1 и дописываем после нее нули в количестве 1 гугола. Записать это число можно, как 10^10^100. В десятичной форме его невозможно изобразить, так как, если все пространство Вселенной заполнить листками бумаги, на каждом из которых были бы написаны 0 с размером «вордовского» шрифта 10, то и в этом случае получилась бы лишь половина всех 0 после 1 для числа гуголплекс.
• 10^10^10^10^10^1.1. Это число, показывающее количество лет, через которые согласно теореме Пуанкаре наша Вселенная в результате случайных квантовых колебаний вернется в состояние близкое к сегодняшнему дню.

Как появились числа Грэма

В 1977 году известный популяризатор науки Мартин Гарднер в журнале Scientific American опубликовал заметку, касающуюся доказательства Грэма одной из проблем теории Рамсе. В ней он назвал границу, установленную ученым, наибольшим числом, когда-либо использовавшимся в серьезном математическом рассуждении.

Кто такой Рональд Льюис Грэм

Ученый, которому сегодня уже за 80, родился в Калифорнии. В 1962 году он получил степень Ph.D в области математики в университете Беркли. В течение 37 лет он работал в лаборатории Белла, а позже перешел в АТ&Т Labs. Ученый активно сотрудничал с одним из величайших математиков 20-го века Палом Эрдешем и является лауреатом многих престижных премий. В научной библиографии Грэма более 320 научных работ.

В середине 70-х годов ученого заинтересовала проблема, связанная с теорией Рамсея. При ее доказательстве была определена верхняя граница решения, являющаяся очень большим числом, впоследствии названным в честь Рональда Грэма.

Проблема гиперкуба

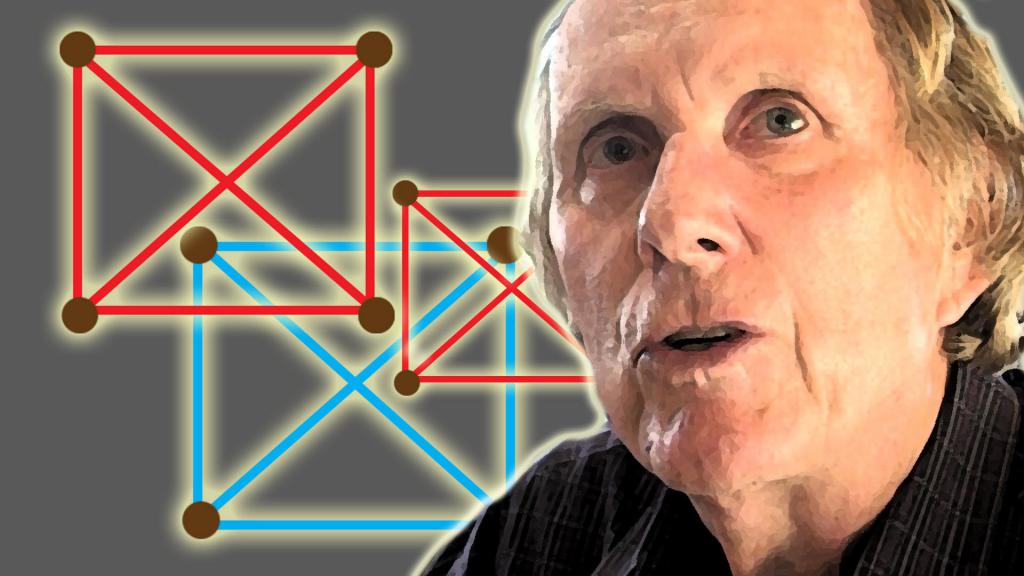
Чтобы понять суть числа Грэма, нужно сначала разобраться с тем, как оно было получено.

Ученый и его коллега Брюс Ротшильд занимались решением следующей задачи:

• Имеется n-мерный гиперкуб. Все пары его вершины соединяют так, чтобы получился полный граф с 2ⁿ вершинами. Каждое его ребро раскрашивают либо в синий, либо в красный цвет. Требовалось найти, какое наименьшее число вершин должно быть у гиперкуба, чтобы каждая такая раскраска содержала полный одноцветный подграф с 4 вершинами, лежащими в одной плоскости.

Решение

Грэм и Ротшильд доказали, что задача имеет решение N’, удовлетворяющее условию 6 ⩽ N’ ⩽N где N — это точно определенное, очень большое число.

Нижняя граница для N впоследствии была уточнена другими учеными, доказавшими, что N должно быть больше или равно 13. Таким образом, выражение для наименьшего числа вершин гиперкуба, удовлетворяющего условиям, представленным выше, получило вид 13 ⩽ N’⩽ N.

Стрелочная нотация Кнута

Перед тем как дать определение числа Грэма, следует ознакомиться со способом его символьного представления, так как ни десятичная, ни двоичная запись для этого абсолютно не пригодны.

На данный момент для представления этой величины принято использовать стрелочную нотацию Кнута. Согласно ей:

a^b=a "стрелка вверх" b.

Для операции многократного возведения в степень была введена запись:

a "стрелка вверх" "стрелка вверх" b= а^b="башня, состоящая из а в количестве b шт."

А для пентации, т. е. символьного обозначения повторного возведения в степень предыдущего оператора, Кнут использовал уже 3 стрелки.

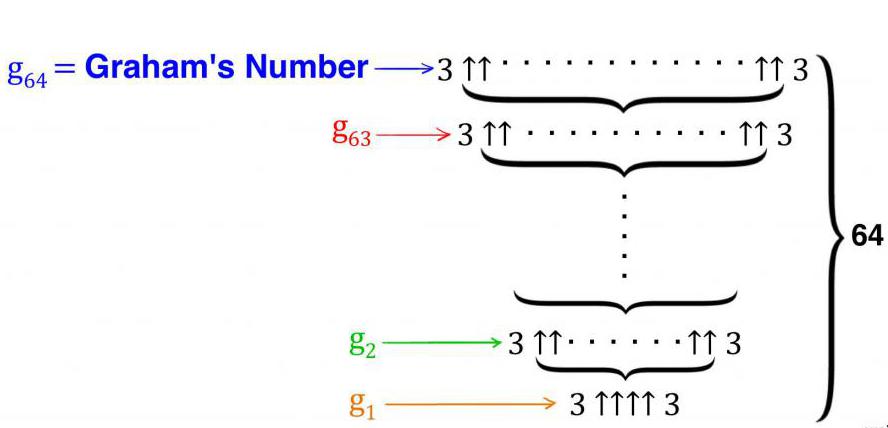
Используя такой вариант записи для числа Грэма, имеем "стрелочные" последовательности, вкладывающиеся друг в друга, в количестве 64 шт.

Масштаб

Свое известное число, которое волнует воображение и расширяет границы человеческого сознания, выводя его за пределы Вселенной, Грэм и его коллеги получили его в качестве верхней границы для числа N при доказательстве проблемы гиперкуба, представленной выше. Представить сколь велик его масштаб обычному человеку крайне сложно.

Вопрос о количестве знаков, или как иногда ошибочно говорят, нулей в числе Грэма, интересует практически всех, кто впервые слышит об этой величине.

Достаточно сказать, что имеем дело со стремительно растущей последовательностью, которая состоит из 64 членов. Даже ее первый член — невозможно представить, так как он состоит из n "башен", состоящих из 3-к. Уже ее "нижний этаж" из 3 троек равен 7 625 597 484 987, т. е. превосходит 7 миллиардов, что и говорить о 64-м этаже (не члене!). Таким образом, точно сказать, чему равно число Грэма, на данный момент невозможно, так как для его вычисления не хватит объединенных мощностей всех компьютеров, существующих на Земле на сегодняшний день.

Рекорд побит?

В процессе доказательства теоремы Краскала, число Грэма было “сброшено с пьедестала”. Ученый предложил следующую задачу:

• Имеется бесконечная последовательность конечных деревьев. Краскал доказал всегда существует участок какого-то графа, являющийся одновременно и частью большего графа и его точной копией. Это утверждение не вызывает никаких сомнений, так как очевидно, что в бесконечности всегда найдется точно повторяющаяся комбинация.

Позже Харви Фридман несколько сузил эту задачу, рассмотрев только такие ациклические графы (деревья), что для конкретного из них с коэффициентом i есть не более чем (i + k) вершин. Он решил выяснить, каково должно быть число ациклических графов, чтобы при этом способе их задачи всегда можно было найти такое поддерево, которое вкладывалось бы в другое дерево.

В результате исследований этого вопроса было выяснено, что N в зависимости от k растет с огромной скоростью. В частности, если k = 1 то N = 3. Однако при k = 2, N уже достигает 11. Самое интересное начинается, когда k = 3. В таком случае N стремительно "взлетает" и достигает величины, которая многократно превосходит число Грэма. Чтобы представить насколько она велика, достаточно записать число, рассчитанное Рональдом Грэмом в виде G64(3). Тогда величина Фридмана-Краскала (об. FinKraskal(3)), будет иметь порядок G(G(187196)). Иными словами получается мегавеличина, которая бесконечно больше невообразимо большого числа Грэма. В то же время даже оно в гигантское число раз будет меньше бесконечности. Об этом понятии имеет смысл поговорить поподробнее.

Бесконечность

Теперь, когда мы объяснили, что такое число Грэма на пальцах, следует разобраться со смыслом, который вкладывался и вкладывается в это философское понятие. Ведь “бесконечность” и “бесконечно большое число” в определенном контексте можно считать тождественными.

Наибольший вклад в изучение этого вопроса сделал Аристотель. Великий мыслитель древности разделил бесконечность на потенциальную и актуальную. Под последней он подразумевал реальность существования бесконечных вещей.

По мнению Аристотеля, источниками представлений об этом фундаментальном понятии являются:

• время;
• разделение величин;
• понятие границы и существования чего-то за ее пределами;
• неиссякаемость творящей природы;
• мышление, которое не имеет пределов.

В современной трактовке для бесконечности нельзя указать количественную меру, так что поиски самого большого числа можно продолжать вечно.

Заключение

Можно ли считать метафору "Взгляд в бесконечность" и число Грэма в некотором смысле синонимами? Скорее, и да и нет. И то и другое невозможно представить, даже имея самое сильное воображение. Однако, как уже было сказано, оно не может считаться "самым, самым". Другое дело, что на данный момент величины больше числа Грэма не имеют установленного физического смысла.

Кроме того, оно не обладает такими свойствами бесконечного числа ¥, как:

• ∞ + 1 = ∞;
• существует бесконечное число как нечетных, так и четных чисел;
• ∞ - 1 = ∞;
• количество нечетных чисел составляет ровно половину от всех чисел;
• ∞ + ∞ = ∞;
• ∞/2 = ∞.

Подытожим: число Грэма самое большое число в практике математического доказательства, по версии Книги рекордов Гиннеса. Однако существуют числа, которые в разы больше этой величины.

Скорее всего, в будущем появится нужда в еще больших «гигантах», особенно если человек выйдет за пределы нашей Солнечной системы или изобретет нечто невообразимое на нынешнем уровне нашего сознания.